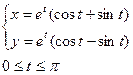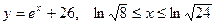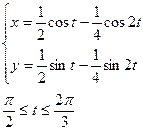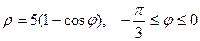1. 
Жауабы: 8
2. 
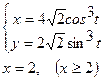
Жауабы: 
3. 
Жауабы: 9
4. 
Жауабы: 
5. 
Жауабы: 
6. 
Жауабы: 
7. 
Жауабы: 
8. 
Жауабы: 
9. 
Жауабы: 1
10. 
Жауабы: 
11. 
Жауабы: 1/6
12. 
Жауабы:3 
13. 
Жауабы: 9
14. 
Жауабы: 
15. 
Жауабы: 1
16. 
Жауабы: 
17. 
Жауабы: 
18. 
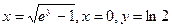
Жауабы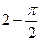 
19. 
Жауабы: 
20. 
Жауабы: 
21. 
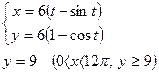
Жауабы: 
22. 
Жауабы: 
23. 
Жауабы:
24. 
Жауабы: 2
25. 
Жауабы: 
Жазық қисық доғасының ұзындығы.
1. 
Жауабы: 1
-
Жауабы: 20 -
Жауабы: 
Жауабы 
-
Жауабы: 48 -
Жауабы 
-
Жауабы: 1 -
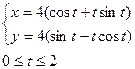Жауабы: 8 -
Жауабы: 
Жауабы: 
Жауабы: 
Жауабы: 
-
Жауабы: 
-
Жауабы: 15
Жауабы: 
Жауабы: 
Жауабы: 
- .
Жауабы: -
Жауабы: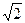 
-
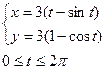Жауабы: 6 -
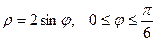
Жауабы: 
Жауабы: 
Жауабы: 
Жауабы: 
Жауабы: 
Айналу денелерінің көлемі.
Берілген функциялардың графиктерімен шектелген фигуралардың координаттық осьтерді айналуынан пайда болған денелердің көлемін табыңыз. 1-15 нұсқаларында Ох өсі, 16-25 нұсқаларында Оу өсі.
1. 
2. 
3. 
4. 
5. 
6. 
7. 
8. 
9. 
10. 
11. 
12. 
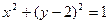
13. 
14. 
15. 
16. 
17. 
18. 
19. 
20. 
21. 
22. 
.
23. 
24. 
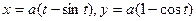және 
осімен.
25. 
Жеке тапсырма №9
Тақырыбы: «Дифференциалдық теңдеулер».
Ші ретті дифференциалдық теңдеулер».
«Жоғарғы ретті дифференциалдық теңдеулер»
Тапсырма:
1. Айнымалылары ажыратылатын дифференциалдық теңдеулердің жалпы шешімін табыңыз.
2. Біртекті дифференциалдық теңдеулер.
3. 1-ші ретті сызықтық дифференциалдық теңдеулер.
4. Жоғарғы ретті дифференциалдық теңдеулер.
5. Біртекті емес дифференциалдық теңдеулердің жалпы шешімін табу керек.
Айнымалылары ажыратылатын дифференциалдық теңдеулердің жалпы шешімін табыңыз
1. 
2. 
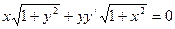
3. 
4. 
5. 
6. 
7. 
8. 
9. 
10. 
11. 
12. 
13. 
14. 
15. 
16. 
17. 
18. 
19. 
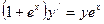
20. 
21. 
22. 
23. 
24. 
25. 
Біртекті дифференциалдық теңдеулер
1. 
2. 
3. 
4. 
5. 
6. 
7. 
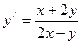
8. 
9. 
10. 
11. 
12. 
13. 
14. 
15. 
16. 
17. 
18. 
19. 
20. 
21. 
22. 
23. 
24. 
25. 
Бірінші ретті сызықтық дифференциалдық теңдеулер
1. 
2. 
3. 
4. 
5. 
6. 
7. 
8. 
9. 
10. 
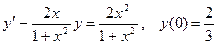
11. 
12. 
13. 
14. 
15. 
16. 
17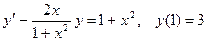 
18. 
19. 
20. 
21. 
22. 
23. 
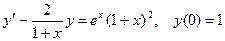
24. 
25. 
Жоғарғы ретті дифференциалдық теңдеулер
1. 
2. 
3. 
4. 
5. 
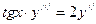
6. 
7. 
8. 
9. 
10. 
11. 
12. 
13.. 
14. 
15. 
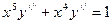
16. 
17. 
18. 
19. 
20. 
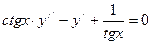
21. 
22. 
23. 
24. 
25. 
Біртекті емес дифференциалдық теңдеулердің жалпы шешімін табыңыз
1. 
2. 
3. 
4. 
5. 
6. 
7. 
8. 
9. 
10. 
11. 
12. 
13. 
14. 
15. 
16. 
17. 
18. 
19. 
20. 
21. 
22. 
23. 
24. 
25. 
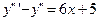
Біртекті емес дифференциалдық теңдеулердің жалпы шешімін табыңыз
1. 
2. 
3. 
4. 
5. 
6. 
7. 
8. 
9. 
10. 
11. 
12. 
13. 
14. 
15. 
16. 
17. 
18. 
19. 
20. 
21. 
22. 
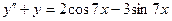
23. 
24. 
25. 
Әдебиет: 1,2,6,7,11,14,16,22, 23,26,27.
Жеке тапсырма №10
Тақырыбы: «Екі еселі интеграл». «Екі еселі интегралдың қолданылуы»
Тапсырма:
1. Екі еселі интегралды есептеу.
2. Интегралдау ретін өзгерту.
3. Фигураның ауданын табу.
1. Есептеңіз:
1. 
; 
. Жауабы:1.
2. 
; 
. Жауабы: 2.
3. 
; 
. Жауабы: 1.
4. 
; 
. Жауабы: 1.
5. 
; 
. Жауабы: 2.
6. 
; 
. Жауабы: 3.
7. ; 
. Жауабы: 1.
8. 
; 
. Жауабы: 4.
9. 
; 
. Жауабы: 0.
10. 
; . Жауабы: 2.
11. 
; . Жауабы: 2.
12. 
; . Жауабы: 8.
13. 
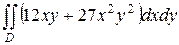; . Жауабы: 2.
14. 
; . Жауабы: 3.
15. 
; . Жауабы: 0.
16. 
; . Жауабы: 1.
17. 
; . Жауабы: -1.
18. 
; . Жауабы:1.
19. 
; . Жауабы: 1.
20. ; . Жауабы: -1.
2. Интегралдау ретін өзгерту:
1. 
. Жауабы: 
2. 
. Жауабы: 
+ 
3. 
. Жауабы: 
+ 
4. 
. Жауабы: 
+ 
5. 
. Жауабы: 
+ 
6. 
.
Жауабы: 
+ 
+ 
7. 
. Жауабы: 
+ 
8. 
. Жауабы: 
9. 
. Жауабы: 
10. 
. Жауабы: 
11. 
. Жауабы: 
+ 
12. 
. Жауабы: 
+ 
13. 
+ 
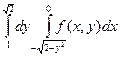. Жауабы: 
14. 
+ 
Жауабы: 
15. 
+ 
Жауабы: 
16. 
+ 
Жауабы: 
17. 
+ 
Жауабы: 
18. 
+ 
Жауабы: 
19. 
+ 
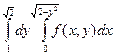Жауабы: 
20. 
+ 
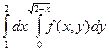Жауабы: 
3. Берілген сызықтармен шектелген фигуралардың аудандарын табыңыз:
1. 
. Жауабы: 
2. 
. Жауабы: 
3. 
. Жауабы: 
4. 
, 
. Жауабы: 
5. 
. Жауабы: 
6. 
. Жауабы: 
7. 
. Жауабы: 
8. 
Жауабы: 
9. 
Жауабы: 
10. 
. Жауабы: 
11. 
. Жауабы: 
12. 
. Жауабы: 
13. 
. Жауабы: 
14. 
. Жауабы: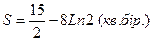 
15. 
. Жауабы: 
16. 
Жауабы: 
17. 
Жауабы: 
18. 
Жауабы:
19. 
Жауабы: 
20. 
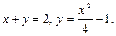Жауабы: 
Әдебиет: 1,2,4,10,14,16,22,23 26,27.
Жеке тапсырма №11
Тақырыбы: «Үш еселі интеграл»
Тапсырма:
1. Үш еселі интегралды есептеу керек.
2. Дененің көлемін табыңыз.
1. Есептеңіз:
1. 
, 
Жауабы: 10
2. 
, 
Жауабы: 0
3. 
, 
Жауабы: 1
4. 
, 
Жауабы: 7
5. 
, 
Жауабы: 12
6. 
, 
Жауабы: 8
7. 
, 
Жауабы: 225
8. 
, 
Жауабы: 5
9. 
, 
Жауабы: 18
10. , Жауабы: 18
11. , Жауабы: 1
12. 
, 
Жауабы: 96
13. 
, 
Жауабы: 64
14. 
, 
Жауабы: 2
15. 
, 
Жауабы: 2
16. 
, 
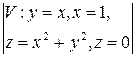Жауабы: 23
17. 
, 
Жауабы: 25
18. 
, 
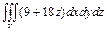Жауабы: 34
19. , Жауабы: 2
20. 
, 
Жауабы: 1
2. Берілген жазықтықтармен шектелген дененің көлемін табу керек:
1. Жазықтықтың координатасымен, х=4, у=4 жазықтықтарымен және 
айналу парболоидымен шектелген.
Жауабы: 
.
2. 
жазықтықтарымен шектелген.
Жауабы: 
.
3. 
жазықтықтарымен шектелген.
Жауабы: 
.
4. 
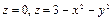жазықтықтарымен шектелген.
Жауабы: 
.
5. 
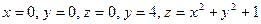жазықтықтарымен шектелген.
Жауабы: .
6. 
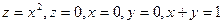жазықтықтарымен шектелген.
Жауабы: 
.
7. 
жазықтықтарымен шектелген.
Жауабы: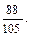 
8. 
жазықтықтарымен шектелген.
Жауабы: 
9. 
жазықтықтарымен шектелген және бірінші октанта орналасқан.
Жауабы: 12.
10. 
жазықтықтарымен шектелген.
Жауабы: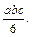 
11. 
жазықтықтарымен шектелген.
Жауабы: 
12. Жазықтықтың координатасымен, 
жазықтығымен және 
цилиндрімен шектелген.
Жауабы: 16.
13. 
жазықтықтарымен шектелген.
Жауабы: 
14. 
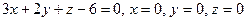жазықтықтарымен шектелген.
Жауабы: 6.
15. 
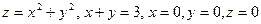жазықтықтарымен шектелген.
Жауабы: 
16. 
жазықтықтарымен шектелген.
Жауабы:
17. 
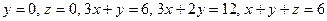жазықтықтармен шектелген.
Жауабы: 12.
18. Жазықтықтың координатасымен, жазықтығымен және 
цилиндрімен шектелген.
Жауабы: 16.
19. 
цилиндрімен, жазықтықтың координатасымен және 
жазықтығымен шектелген.
Жауабы: 45.
20. 
цилиндрімен, жазықтықтың координатасымен және 
жазықтығымен шектелген.
Жауабы: 
Әдебиет: 1,2,4,10,14,16,22,23 26,27.
Жеке тапсырма №12
Тақырыбы: «Қатарлар». «Дәрежелі қатарлар»
Тапсырма:
1. Даламбер және Кошидің белгілерін қолданып қатарларды жинақтылыққа зерттеңіз.
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
| ||
|
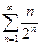
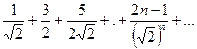
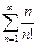
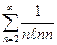
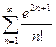
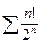
