И.И. Гордеев
к.ф.-м.н., доцент кафедры прикладной математики и информатики
Астраханский государственный университет
Г. Астрахань, Российская Федерация
А.В. Костенко
студент 6-ого года обучения, учитель информатики
Астраханский государственный университет
Г. Астрахань, Российская Федерация
ИСПОЛЬЗОВАНИЕ SCILAB 5.5.2 ДЛЯ ПОСТРОЕНИЯ ГРАФИКОВ С ТОЧКАМИ РАЗРЫВА
В настоящее время среди бесплатных программ, позволяющих проделывать анализ различных математических моделей, наибольшими возможностями обладает программа Scilab. Бесплатность программы Scilab позволяет широко использовать ее в процессе обучения. Последняя стабильная версия программы — 5.5.2, вышедшая 1 апреля 2015 года [1]. Одним из важных этапов анализа математических моделей является построение графиков.
Scilab позволяет строить графики различных функций. Существуют руководства, в том числе на русском языке, описывающие процесс построения графиков в Scilab [2], [3,c. 57-109], но в большинстве руководств возможности Scilab описываются при помощи примеров без подробных пояснений к примерам. Кроме того, в книге Алексеева Е.Р. [3] часть информации относится к устаревшим версиям Scilab, а часть примеров реализуется на основе чисто формального импорта примеров из Matlab — аналогичной программы, имеющей несколько больше возможностей, но являющаяся платной [4]. Поэтому мы постараемся привести несколько своих примеров использования последней версии Scilab для построения графиков, подробно поясняя используемый код и используемые приемы.
Пример 1. Построение графика синусоиды.
0001 x=-2*%pi:0.1:2*%pi;0002 y=sin(cos(x));0003 plot (x,y);0004 xtitle('график функции y=sin(cos(x))', 'X','Y');Результат построения графика приведен на рисунке 1.
Рис.1. Простейшее построение графика синусоиды.
Для построения графика необходимо задать два массива: значения x и значения y. Именно это делается в первых двух строчках кода: в первой строчке задается массив x, а во второй строчке вычисляется массив значений y путем применения функции синус к массиву x. Третья строчка выполняет построение графика в отдельном окне. При построении графика точки, указанные в массивах, соединяются последовательно непрерывной линией. Четвертая строчка задает общую подпись к графику и подписи к осям.
Рассмотрим более сложный пример — построение графика гиперболы, задаваемой уравнением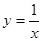 
Особенностью данного примера является то, что функция имеет разрыв при 
. Попытка вычислить функцию в данной точке приведет к ошибке. Поэтому возникает два вопроса: как избежать вычисления функции в точке разрыва и как избежать соединения между собой частей графика, которые не должны соединяться. Для решения этой задачи можно использовать два массива точек по x: один массив содержит значения x левее точки разрыва, а другой массив содержит значения x правее точки разрыва. Для каждого из двух массивов x вычисляются соответственно два массива со значениями y и затем каждая пара массивов по x и y используется для построения своей части графика. Далее приводится полный код примера 2.
Пример 2. Построение графика гиперболы.
0001 x1=-9.95:0.1:0;0002 y1=x1.\1;0003 plot (x1,y1);0004 x2=0.05:0.1:9.95;0005 y2=x2.\1;0006 plot (x2,y2);0007 a= gca ();0008 a.y_label.font_angle = 0;
0009 a.x_location='origin';0010 a.y_location='origin';0011 a.data_bounds=[-10,-20;10,20];0012 a.tight_limits = 'on';0013 a.box='off';0014 a.x_label.position=[11,0];0015 a.y_label.position=[1,19];0016 xtitle('график гиперболы', 'X','Y');
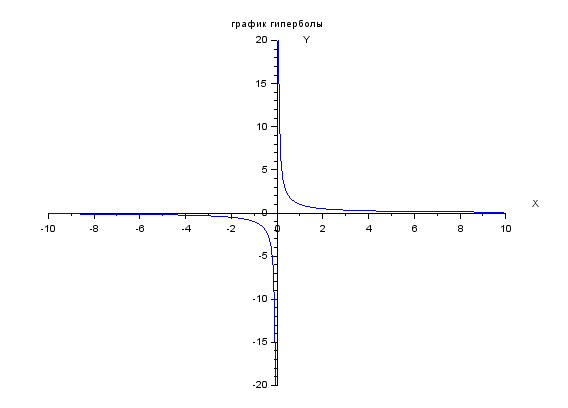
Рис.2. Построение графика гиперболы с учетом разрыва.
График, который строится в результате выполнения программы из примера 2 показан на рисунке 2. В строчках 1-3 задаются массивы x и y и делается построение для левой части гиперболы, аналогично строчкам 1-3 в программе построения синусоиды. Пояснения требует операция, используемая во второй строчке: «x1.\1». Комбинация символов «.\» с последующим числом означает поэлементное формирование нового массива путем деления указанного числа на каждой элемент массива, указанного перед операцией. Данная операция называется поэлементным левым делением [3, c. 33].
Аналогично в строчках 4-6 строится правая часть гиперболы на том же графике. В строчке 16 задается подпись к графику и подписи к осям (аналогично четвертой строчке программы для синусоиды).
В строчках 7-15 выполняется тонкая настройка свойств графика. Если посмотреть на рисунок 2, то его вид в плане оформления графика существенно отличается от рисунка 1. В частности, изображение осей помещено не с краю, а по центру, в традиционном для математических графиков виде. Подписи к осям сделаны не посредине оси, а в традиционном для математики виде (подпись «y» вверху вертикальной оси, подпись «x» справа от горизонтальной оси). В седьмой строчке вызывается функция gca() для того чтобы запомнить в переменной «a» ссылку на объектную переменную, соответствующую осям (gca является аббревиатурой от «get current axes» – «получить текущие оси»). В строчках 8-15 выполняется настройка различных свойств осей. В частности, строчка 8 необходима, чтобы подпись к оси «y» рисовалась прямо, а не повернутой набок. Угол поворота подписи задается в градусах, отсчет ведется по часовой стрелке, нулевой угол соответствует прямой подписи. Строчки 9 и 10 задают, что оси x и y должны рисоваться проходящими через начало координат (0,0), а не сбоку от графика. В строке 11 задаются границы по осям x и y, в которых должен рисоваться график. В строке 12 указывается, что именно указанные границы должны быть строгими ограничениями (не должно быть пустого места за пределами границ). Строчка 13 отключает рамку обводящую весь график. Строчки 14 и 15 задают положение подписей к осям в используемой системе координат.
Существует альтернативный способ построения графиков путем оформления в Scilab функции, график которой требуется построить. Подобный прием описывается у Микаэля Бодена (Michaël Baudin) [5, с. 71], однако об особенностях построения графиков, имеющих точки разрыва, Боден тоже не делает никаких указаний. Поэтому мы покажем сочетание приема с оформлением функции и описанного выше приема для построения графика имеющего разрыв. Соответствующий код приведен в примере 3.
Пример 3. Построение графика гиперболы с определением функции.
0001 function f = mygiperbola (x)
0002 f = 1/ x
0003 endfunction
0004 x1=-9.95:0.1:0;
0005 plot (x1, mygiperbola);
0006 x2=0.05:0.1:9.95;
0007 plot (x2, mygiperbola);
0008 a= gca ();
0009 a.y_label.font_angle = 0;
0010 a.x_location='origin';
0011 a.y_location='origin';
0012 a.data_bounds=[-10,-20;10,20];
0013 a.tight_limits = 'on';
0014 a.box='off';
0015 a.x_label.position=[11,0];
0016 a.y_label.position=[1,19];
0017 xtitle('график гиперболы', 'X','Y');
В строчках 1-3 определяется правило вычисления функции 
. Функции дается имя mygiperbola, которое затем используется в качестве второго аргумента функции plot в строчках 5 и 7. Построение также разбивается на две части: в строчках 4-5 строится левая часть гиперболы до разрыва, а в строчках 6-7 строится правая часть гиперболы после разрыва. При данном способе построения, достаточно задать только массив точек по х, а значения по у вычисляется сама функция plot, используя переданное ей имя функции mygiperbola.
Список использованной литературы:
1. Scilab 5.5.2 Release / 2015 / News / Community / Home – Scilab / URL: http://www.scilab.org/content/view/full/1339 (дата обращения 23.10.2015).
2. Scilab/Графики — Викиучебник / URL: https://ru.wikibooks.org/wiki/
Scilab/Графики (дата обращения 23.10.2015).
3. Алексеев Е.Р., Scilab: Решение инженерных и математических задач / Е.Р. Алексеев, О.В. Чеснокова, Е.А. Рудченко. — М.:ALT Linux; БИНОМ. Лаборатория знаний, 2008. — 269 с.
4. How to Buy MATLAB and Simulink / URL: https://www.mathworks.com/store/default.do?s_cid=store_top_nav&s_tid=gn_store (дата обращения 23.10.2015).
5. Baudin M., Введение в Scilab. — 2013. — 89 c. / URL: http://forge.scilab.org/index.php/p/docintrotoscilab/downloads/get/introscilab-v1.4-ru.pdf
© И.И. Гордеев, А.В. Костенко, 2015
