Площадь полной поверхности

Примеры тел вращения

Шар — образован полукругом, вращающимся вокруг диаметра разреза
Цилиндр — образован прямоугольником, вращающимся вокруг одной из сторон

За площадь боковой поверхности цилиндра принимается площадь его развертки: Sбок = 2πrh.

Конус — образован прямоугольным треугольником, вращающимся вокруг одного из катетов

За площадь боковой поверхности конуса принимается площадь ее развертки: Sбок = πrl Площадь полной поверхности конуса: Sкон = πr(l+ r)

Тор — образован окружностью, вращающейся вокруг прямой, не пересекающей его ^[2]

При вращении контуров фигур возникает поверхность вращения (например, сфера, образованная окружностью), в то время как при вращении заполненных контуров возникают тела (как шар, образованный кругом).

Сфе́ра (греч. σφαῖρα — мяч) — замкнутая поверхность, геометрическое место точек в пространстве, равноудалённых от данной точки, называемой центром сферы. Сфера также является телом вращения, образованным при вращении полуокружности вокруг своего диаметра. Площадь сферы в градусной мере с учётом непостоянства значения размеров дуг составляет 41252,96 кв. градусов.

Сфера является частным случаем эллипсоида, у которого все три оси (полуоси, радиусы) равны. Сфера является поверхностью шара.

Объём цилиндра, объем вписанной в него сферы, касающейся обоих его оснований, и удвоенный объем конуса, с вершиной в центре одного основания цилиндра и с основанием, совпадающим с другим основанием цилиндра, находятся в соотношении 3:2:1^[1]

Сферическая геометрия

Большой круг — это круг, который делит шар (сферу) на две равные половины. Центр большого круга всегда совпадает с центром сферы. На глобусе, к примеру, все меридианы являются большими кругами. А вот из параллелей только экватор является большим кругом. Все остальные параллели — это малые круги.

Большие круги на поверхности сферы играют роль, аналогичную роли прямых в планиметрии. Кратчайший путь между любыми двумя точками пройдёт по линии большого круга.

Через любые две точки на поверхности сферы, кроме диаметрально противоположных, можно провести единственный большой круг. Через диаметрально противоположные точки на сфере можно провести сколько угодно больших кругов.

Любые два больших круга пересекаются по прямой, проходящей через центр сферы, а окружности больших кругов пересекаются в двух диаметрально противоположных точках.

При пересечении двух больших кругов образуются четыре сферических двуугольника. Площадь двуугольника определяется формулой , где — радиус сферы, а — угол двуугольника.

Три больших круга, не пересекающихся в одной точке, образуют восемь сферических треугольников. Сферический треугольник, все стороны которого меньше половины большого круга, называется эйлеровым. Помимо трёх признаков равенства плоских треугольников, для сферических треугольников имеет место ещё один: два сферических треугольника равны, если их соответствующие углы равны.

Стороны сферического треугольника измеряют величиной угла, образованного радиусами сферы, проведёнными к концам данной стороны. Каждая сторона сферического треугольника меньше суммы и больше разности двух других. Сумма всех сторон сферического треугольника всегда меньше 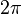. Сумма углов сферического треугольника всегда меньше 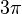и больше . Величина называется сферическим избытком. Площадь сферического треугольника определяется по формуле Жирара .

Соотношения между элементами сферического треугольника изучает сферическая тригонометрия.

ТОР

Площадь поверхности тора как следствие из первой теоремы Гюльдена: .

Объём тела, ограничиваемого тором (полнотория), как следствие из второй теоремы Гюльдена: .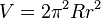

Поверхностью цилиндра, ось которого совпадает с осью тора, а радиус равен среднему радиусу тора, тор может быть разделён на внутреннюю и наружную части. Сравнивая эти части, можно визуально увидеть, что площадь поверхности и объём внутренней части тора меньше площади поверхности и объёма наружной части тора. Площадь поверхности наружной части тора равна , площадь поверхности внутренней части равна: .

Для определения объёма тела какой-либо части тора надо эту часть тора вписать в «катушку» с двумя наружными или внутренними фланцами в зависимости от выбранной части тора. Затем надо определить объём тела выбранной части «катушки» и умножить на ¶/4, т.е. умножить на 0,7853981....

Тор с вырезанным диском («проколотый») можно вывернуть наизнанку непрерывным образом (топологически, то есть серией диффеоморфизмов). При этом две пересекающиеся перпендикулярно окружности на нём («параллель» и «меридиан») поменяются местами.^[1]

Этапы выворачивания тора

Анимация, показывающая разрезание тора бикасательной плоскостью и две получающиеся окружности Вилларсо

Два таких «дырявых» тора, сцепленных между собой, можно продеформировать так, чтобы один из торов «проглотил» другой.^[2]

Вариант окраски участков тора

Минимальное число цветов, необходимое для раскрашивания участков тора так, чтобы соседние были разного цвета, равно 7. См. также Проблема четырёх красок.

Сечения

При сечении тора бикасательной плоскостью, получающаяся кривая четвёртого порядка оказывается вырожденной: пересечение является объединением двух окружностей называемых окружностями Вилларсо.

В частности открытый тор может быть представлен как поверхность вращения окружности зацепленной за ось вращения

Одно из сечений открытого тора — лемниската Бернулли, другие кривые линии являются графическими линиями и называются кривыми Персея^[3] (спирическими линиями, сечениями тора плоскостью, параллельной его оси)
Некоторые пересечения поверхности тора плоскостью внешне напоминают эллипс (кривую 2-го порядка). Получаемая таким образом кривая выражается алгебраическим уравнением 4-го порядка^[4].

Цили́ндр (др.-греч. κύλινδρος — валик, каток) — геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими её. Цилиндрическая поверхность — поверхность, получаемая таким поступательным движением прямой (образующей) в пространстве, что выделенная точка образующей движется вдоль плоской кривой (направляющей). Часть поверхности цилиндра, ограниченная цилиндрической поверхностью называется боковой поверхностью цилиндра. Другая часть, ограниченная параллельными плоскостями, это основания цилиндра. Таким образом, граница основания будет по форме совпадать с направляющей.

В большинстве случаев под цилиндром подразумевается прямой круговой цилиндр, у которого направляющая — окружность и основания перпендикулярны образующей. У такого цилиндра имеется ось симметрии.

Другие виды цилиндра — (по наклону образующей) косой или наклонный (если образующая касается основания не под прямым углом); (по форме основания) эллиптический, гиперболический, параболический.

Призма также является разновидностью цилиндра — с основанием в виде многоугольника.

Площадь бок. поверхность

Площадь боковой поверхности цилиндра равна длине образующей, умноженной на периметр сечения цилиндра плоскостью, перпендикулярной образующей.

Площадь боковой поверхности прямого цилиндра вычисляется по его развёртке. Развёртка цилиндра представляет собой прямоугольник с высотой и длиной , равной периметру основания. Следовательно, площадь боковой поверхности цилиндра равна площади его развёртки и вычисляется по формуле:

В частности, для прямого кругового цилиндра:

, и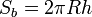

Для наклонного цилиндра площадь боковой поверхности равна длине образующей, умноженной на периметр сечения, перпендикулярного образующей:

Простой формулы, выражающей площадь боковой поверхности косого цилиндра через параметры основания и высоту, в отличие от объёма, к сожалению, не существует.

Площадь полной поверхности

Площадь полной поверхности цилиндра равна сумме площадей его боковой поверхности и его оснований.

Для прямого кругового цилиндра:

ОБЪЕМ

Объём цилиндра

Для наклонного цилиндра существуют две формулы:

Объём равен длине образующей, умноженной на площадь сечения цилиндра плоскостью, перпендикулярной образующей.

Объём равен площади основания, умноженной на высоту (расстояние между плоскостями, в которых лежат основания):

где — длина образующей, а — угол между образующей и плоскостью основания. Для прямого цилиндра .

Для прямого цилиндра , и , и объём равен:

Для кругового цилиндра:

где d — диаметр основания.