Классическое определение вероятности события
Вероятность события А равна отношению числа элементарных исходов, благоприятствующих появлению события А к общему числу элементарных исходов:
.
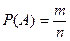Свойства вероятности события:
1) 
. 2) 
. 3) 
.
Практически невозможным называется такое событие, вероятность которого очень мала (близка к нулю).
Практически достоверным называется такое событие, вероятность которого достаточно большая (близка к единице).
Статистической вероятностью события А называется относительная частота появления этого события в n произведенных испытаниях:
,
где m – число испытаний, в которых появилось событие А.
Геометрическое определение вероятности
Пусть отрезок l составляет часть отрезка L. На отрезок L наудачу поставлена точка. Вероятность попадания точки на отрезок l определяется равенством:
Пусть плоская фигура g составляет часть плоской фигуры G. На фигуру G наудачу брошена точка. Вероятность попадания этой точки на фигуру g определяется равенством:
Суммой событий А и В называется такое событие С = А + В, которое означает наступление или А, или В, т.е. хотя бы одного из них.
Произведением событий А и В называется событие С = А × В, состоящее в совместном наступлении события А и события В.
Разностью событий А и В называется событие С = А – В, состоящее в наступлении события А и не наступлении события В.
Число размещений из n элементов по m равно:
Число перестановок из n элементов равно:
Число сочетаний из n элементов по m равно:
Основные теоремы
Теорема сложения вероятностей событий
Для несовместных событий:
Для произвольных событий:
Следствие 1. Сумма вероятностей событий, образующих полную группу, равна единице.
Следствие 2. Сумма вероятностей противоположных событий равна единице.
Вероятность события В, найденная при условии, что событие А произошло, называется условной вероятностью события В.
Два события А и В называются независимыми, если появление одного из них не меняет вероятности появления другого:
Теорема умножения вероятностей событий
Вероятность совместного появления двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже наступило:
Формула полной вероятности
Если событие А может произойти только при появлении одного из событий (гипотез) Н 1, Н 2, …, Hn образующих полную группу, то
Формула Байеса
Если произошло событие А, которое может появиться только с одной из гипотез Н 1, Н 2, …, Hn образующих полную группу событий, то условные вероятности гипотез определяются по формуле:
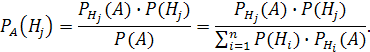
Повторные испытания
Повторные испытания – это последовательное проведение n раз одного и того же опыта или одновременное проведение n одинаковых опытов.
Последовательностью независимых испытаний (схемой Бернулли) называют повторные испытания, удовлетворяющие следующим условиям:
1) в каждом испытании может появится только два исхода: наступит некоторое событие А (успех), либо наступит его дополнение 
(неудача);
2) испытания являются независимыми, т.е. вероятность успеха в m -м испытании не зависит от исходов всех испытаний до m -го;
3) вероятность успеха во всех испытаниях постоянна 
(вероятность неудачи в каждом испытании обозначают q: 
.
При рассмотрении схемы испытаний Бернулли основной задачей является нахождение вероятности 
– вероятность того, что в n независимых испытаниях событие А наступит точно m раз (0 ≤ m ≤ n).
Формула Бернулли
,
где 
, 
.
Число 
наступления события А в n независимых испытаниях называется наивероятнейшим, если вероятность осуществления этого события 
, по крайней мере, не меньше вероятности других событий при любом m:
Формула Пуассона
Если число испытаний неограниченно увеличивается (
), вероятность p наступления события А в каждом испытании неограниченно уменьшается (
), но так, что их произведение np является постоянной величиной (
– const), то:
На практике используется приближенное равенство:
, 
когда вероятность 
успеха мала, т.е. успех является редким событием, а количество испытаний n – велико: 
и 
.
В тех случаях, когда число испытаний n – велико, а вероятность успеха p – не близка к нулю (
), для вычисления используют теоремы Муавра-Лапласа.
Локальная теорема Муавра-Лапласа
Если вероятность p наступления события А в каждом испытании постоянна и отлична от нуля и единицы, а число независимых испытаний достаточно велико (, 
, ), то имеет место приближенное равенство:
– функция Гаусса (плотность стандартного нормального распределения).
Приближенное равенство тем точнее, чем больше n. На практике проверяется условие: 
Свойства функции Гаусса:
1) – функция четная: 
;
2) при 
, – монотонно убывает;
3) при 
, 
(на практике считают, что при 
, 
).
