Абсолютная и относительная погрешность
Абсолютная погрешность меры 
– алгебраическая разность между ее номинальных 
и действительных 
значениями.
Абсолютная погрешность измерительного прибора – алгебраическая разность между показанием прибора 
и действительного значения измеряемой величины.
Погрешность меры: 
Погрешность измерительного прибора: 
Степень точности средства измерений характеризует относительная погрешность 
– выраженное в 
отношении абсолютная погрешность к действительному значению измеряемой или воспроизводимой данным средством измерительной величины.
Погрешности показывают отличие номинальных значений мер и показаний измерительных приборов от их истинных значений, вследствие воздействия большого числа случайных и детерминированных факторов, возникающих в процессе изготовления, хранения и эксплуатации измерительных средств, а также в самом процессе измерения.
Статические методы обработки результатов эксперимента
1. Многократные прямые равноточные измерения:
Обработка результатов включает следующие этапы:
· вычисление среднеарифметического значения:
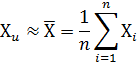
· вычисление среднеквадратического отклонения 
от значений погрешности измерений:
· определяют закон распределения случайной составляющей;
· при заданном значении доверительной вероятности Р (вероятность того, что 
отличается от истинного на величину, не более чем 
) и числе измерений n по таблицам определяем коэффициент Стьюдента 
· находят границы доверительного интервала для случайной погрешности:
· окончательный результат записывается в виде:
при вероятности Р
2. Неравноточные измерения – это измерения одной и той же величины выполненные с различной точностью, разными приборами, в различных условиях.
Для оценки наиболее вероятного значения величин при таком измерении вводят понятие «веса» измерения
Обработка, как в 1 случае.
3. Однократные измерения
Здесь процедура измерений регламентируется заранее, с тем чтобы при известной точности средства измерения и условиях измерения погрешность не превзошла определенное значение, т.е. значения и Р заданы изначально.
Результат измерения запишем:
при Р = 0,05
суммарная погрешность измерения, определяемая классом точности СИ (
и методической погрешностью (
4. Косвенные измерения
Предполагают наличие функциональной связи 
.
Погрешность в оценке Y зависит от погрешности при измерениях аргументов
Абсолютная погрешность: 
Относительная погрешность: 
Среднеквадратическое отклонение: 
Величины 
определяются с помощью коэффициента Стьюдента.
Результат записывается:
при вероятности Р
5. Совместные и совокупные измерения
Совместные – одновременные измерения двух и более величин, если уравнения измерения для этих величин образуют сумму линейных независимых уравнений.
Результаты прямых и косвенных измерений.
Совокупные – одновременные измерения одноименных величин при совместных – разноименных.
