Лабораторная работа № 11
(метод Бесселя)
1. Цель работы: закрепление теоретических знаний по теме 3.1. “Гармонические колебания”,
приобретение практических навыков в определении характеристик колебательных процессов,
изучение методики расчетов величин, характеризующих колебания.
2. Порядок подготовки к выполнению работы: изучить тему и материал лабораторной работы
3. Порядок выполнения лабораторной работы дан в упражнениях
4. Подведение итогов выполнения работы:
предъявить результаты, подготовка и оформление отчета, заполнить таблички, произвести обработку результатов измерений
5. техника безопасности при выполнении лабораторной работы - стандартная
Оборудование: маятник, секундомер, линейка
Теория. Применение оборотного маятника основано на свойстве сопряженности центра качания и точки подвеса. Это свойство заключается в том, что во всяком физическом маятнике можно найти такие две точки, что при последовательном подвешивании маятника за ту или другую из них период колебаний его остается одним и тем же. Расстояние между этими точками определяет собой приведенную длину данного маятника.
Если амплитуда колебаний маятника мала, то время одного простого колебания его, т.е. период колебания, определяется формулой
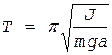 . (4)
. (4)
По теореме о моментах инерции
J = J0+ ma2 , (5)
где J0 - момент инерции относительно оси, проходящей через центр тяжести и параллельной оси качаний, а величины J, m и а те же, что в формуле (2)
Из уравнений
 ,
, 
имеем

Для величины ускорения из последней формулы после преобразований получаем уравнение, данное Бесселем,
 , (6)
, (6)
где l = a1 + a2 - приведенная длина.
Если периоды равны между собой (Т1=Т2=Т), уравнение примет вид (3) 
 .
.
Добиться полного равенства периодов нелегко. Формула Бесселя позволяет достаточно просто и с наименьшей степенью точности определить величину ускорения при приближенном равенстве периодов колебаний.
Пусть Т1 и Т2 близки друг к другу, а величины а1 и а2 сильно отличаются одна от другой (одна чечевица (груз) маятника полая, другая сплошная). В этом случае, как видно из формулы, нет необходимости определять величины а1 и а2 с большой степенью точности (не точнее, чем до 1 мм).
Описание прибора. Оборотные маятники в зависимости от предъявляемых к ним требованиям имеют самую различную форму. Они обычно состоят из металлического стержня длиной свыше 1 м, на поверхности которого нанесены миллиметровые деления. По стержню могут передвигаться и закрепляться в том или ином положении тяжелые и легкие чечевицы (грузы) и опорные призмы. Различные комбинации чечевиц и их положений на стержне с опорными призмами дают различные типы оборотных маятников.
В настоящей задаче применяется оборотный маятник, изображенный на рис.2.
На металлическом стержне А опорные призмы В жестко закреплены и не перемещаются. Жестко закреплена и чечевица С, находящаяся между ними. Вторая чечевица Д находится на конце стержня (не между призмами) и может перемещаться по шкале с нониусом и закрепляться в нужном положении.
Расстояние между призмами постоянно, его значение выбито на стержне.
Измерения. Пользуясь секундомером, определяют периоды колебаний маятника для различных положений чечевицы Д на шкале. Это следует проделать, перемещая чечевицу в пределах от 7 до 12 делений (сантиметров) основной шкалы. В этом интервале необходимо промерить периоды через каждые 5 миллиметров, т.е. получить одиннадцать значений периодов. Каждый период определяется дважды из 100 колебаний, каждый раз пользуются средним арифметическим значением.
Необходимо построить график зависимости периода колебаний от положения чечевицы на стержне маятника, откладывая по оси абсцисс деление шкалы, указывающее положение чечевицы, а по оси ординат величину периода колебаний.
После этого ось вращения маятника изменяют, т.е. заставляют маятник колебаться на другой опорной призме. Вновь, в тех же пределах, с тем же числом измерений, совершенно так же измеряют периоды колебаний. На той же миллиметровой бумаге полученные данные также представляют в виде графика. Точка пересечения кривых определяет местонахождение подвижной чечевицы, которое дает наиболее близкие друг к другу значения периодов.
Для этого положения определяют периоды колебаний Т1 и Т2 (в прямом и перевернутом положении маятника) с наибольшей тщательностью. Определяют время 200 колебаний маятника не менее трех раз, откуда вычисляют период колебаний. Совершенно так же поступают и при определении второго периода(перевернутый маятник). Для определения величин а1 и а2 маятник снимают с консоли и осторожно кладут его стержнем на специальную подставку. На подставке, которая имеет острую грань, маятник необходимо уравновесить. Расстояния от точки центра тяжести маятника, находящейся над гранью, до опорных призм дают величины а1 и а2 . Измерения их производятся масштабной линейкой с точностью до миллиметра.
По полученным данным, пользуясь формулой Бесселя, определяют величину ускорения силы тяжести.
Выполнение работы требует внимания и тщательности. Недопустимы колебания маятника с углом отклонения больше, чем 40.
Контрольные вопросы
1. В чем преимущество метода Бесселя перед другими маятниковыми методами определения величины ускорения свободного падения?

Рис. 1 Общий вид оборотного маятника
Стержни
m1 = 510 г, m2 = 510 г,
L1 = 573 мм L2 = 572 мм
Муфты
m1 = 395 г m1 = 390 г m1 = 420 г m1 = 390 г
l1 = 100 мм l2 = 100 мм l3 = 100 мм l4 = 100 мм
Масса всего маятника 2620 г






