Цифровая обработка изображений

Графическую информацию можно представлять в двух формах: аналоговой или дискретной. Путем разбиения графического изображения на большое количество маленьких цветных фрагментов происходит преобразование графической информации из аналоговой формы в дискретную. При этом производится кодирование – присвоение каждому элементу изображения конкретного значения в форме кода. Общая схема цифровой обработки изображений может быть представлена в следующей последовательности:

1. Получение исходного изображения.

2. Фильтрация изображения.

3. Перевод изображения в необходимую цветовую модель.

4. Форматирование и индексирование изображения.

5. Разбивка на блоки. Обработка информации, содержащейся в блоках.

6. Сжатие изображения.

Получение исходного изображения. Изображения, предназначенные для обработки, условно можно разбить на четыре класса:

1. Естественные, полученные путем сканирования, захвата теле - или видео- кадра, съемкой цифровой аппаратурой.

2. Изображения, нарисованные с использованием графического редактора на компьютере.

3. Трехмерные сцены, синтезированные с помощью специальных программ, таких как: AutoCAD, 3D Studio и т. п.

4. Изображения – визуализация данных, полученных как результат некоторого эксперимента, опыта, измерения (энцефалограмма, сейсмографическая карта).

Естественные изображения имеют некомпьютерное происхождение. В них почти нет резких цветовых переходов.

Компьютерные рисунки подразделяются на следующие типы: растровые, векторные и фрактальные.

Растровая графика. Растровые изображения напоминают лист клетчатой бумаги, на котором любая клетка закрашена либо черным, либо белым цветом, образуя в совокупности рисунок.

Пиксел – основной элемент растровых изображений. Именно из таких элементов состоит растровое изображение.

Важнейшей характеристикой любого растрового изображения является его разрешение – количество пикселов на дюйм изображения (ppi – pixel per inch). Когда говорят о самом изображении, его вводе в компьютер, хранении и обработке, речь идёт о пикселах, и разрешение измеряется в ppi, а вот у всех устройств вывода (мониторов, принтеров, плоттеров) разрешение соответствует шагу точек и измеряется в dpi (число точек на дюйм).

Достоинства растровой графики. Растровая графика эффективно представляет реальные образы. Помимо естественного вида растровые изображения имеют другие преимущества. Устройства вывода (принтеры) для создания изображений используют наборы точек. Растровые изображения могут быть очень легко распечатаны на таких принтерах, потому что компьютерам легко управлять устройством вывода для представления отдельных пикселов с помощью точек.

Недостатки растровой графики. Большие объемы данных – это основная проблема при использовании растровых изображений. Существует так же проблема редактирования растровых изображений, так как большие растровые изображения занимают значительные массивы памяти. Для обеспечения работы функций редактирования таких изображений потребляются так же немалые массивы памяти и другие ресурсы компьютера.

Масштабирование растровых изображений. Одним из недостатков растровой графики является так называемая пикселизация изображений при их увеличении (если не приняты специальные меры) (рис. 4). Если в оригинале присутствует определенное количество точек, то при большем масштабе увеличивается и их размер, становятся заметны элементы растра, что искажает саму иллюстрацию. Для противодействия пикселизации принято заранее оцифровывать оригинал с разрешением, достаточным для качественной визуализации при масштабировании. Другой прием состоит в применении стохастического растра, позволяющего уменьшить эффект пикселизации в определенных пределах. Наконец, при масштабировании используют метод интерполяции, когда увеличение размера иллюстрации происходит путем добавления необходимого числа промежуточных точек.

Рис. 4. Масштабирование растрового изображения

Векторная графика — метод построения изображений, в котором используются математические описания для определения положения и формы геометрических объектов.

Векторную графику можно назвать объектно-ориентированной или структурной, т.е. изображение, выполненное на компьютере, базируется на использовании графических примитивов, которые описывают отдельные элементы рисунка или чертежа: точка, отрезок, окружность, эллипс, кривая и т. д.

Геометрическая модель – совокупность сведений, однозначно задающих форму геометрического объекта. Геометрические модели могут быть заданы системами уравнений линий и поверхностей, алгебраическими соотношениями, графами, списками, таблицами.

Геометрическое моделирование – процесс от описания объекта в соответствии с поставленной задачей до получения внутримашинного представления. Требования, которые должны предъявляться к геометрическому моделированию в компьютерной графике, можно сформулировать следующим образом:

а) модель не должна противоречить реальному объекту (правильность модели);

б) возможность моделирования объекта целиком (мощность модели);

в) возможность вычисления ряда геометрических параметров;

г) минимальное количество информации для представления модели (компактность);

д) использование других функций (расчёт, метод конечных элементов) – открытость.

Геометрические модели бывают двумерные и трёхмерные. Двумерные модели позволяют формировать и изменять рисунки и чертежи, а трёхмерная модель – создать виртуальное представление объекта в трёх измерениях.

Точка. Точка задаётся координатами (x, y, z), которые могут быть представлены вектор-строкой [x, y, z] или вектор-столбцом.

Это геометрические данные. Топологические данные: принадлежность отрезку (SG), дуге (CE), контуру (CO) – в двумерном случае.

В изображениях, выводимых на экран дисплея, очень часто фигурируют отрезки прямых. Для вывода отрезков на экран используются различные устройства, называемые генераторами векторов. В различных генераторах используют различные формы уравнений прямой линии. Обозначим концы отрезка прямой, как (x₁, y₁) и (x₂, y₂). Кроме того, введём обозначения:

DX=X₂ –X₁, (1)

DY=Y₂ –Y_1.

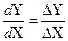Прямая. Уравнение прямой может быть записано в диффференциальной форме:

. (2)

Параметрическая форма задания кривой:

X= (1 – t)×X₁–tX₂, (3)

Y= (1 – t)×Y₁–tY_2.

Параметр t изменяется в диапазоне 0 £ t£ 1.

 

Эллипс и окружность. После отрезков прямых в графических изображениях наиболее часто встречаются окружности и эллипсы. Для получения изображения окружности единственным способом является расчёт и изображение эллипса, т.к. в большинстве графических режимов вертикальный и горизонтальный масштабы различны.

Уравнение эллипса с центром в начале координат и полуосями a и b может быть записано

b²x² + a²y² – a²b² = 0. (4)

Уравнение эллипса с центром в точке (x_с,y_с) имеет вид

b²(x – x_c)² + a²(y – y_c)² – a²b² = 0. (5)

Кривая второго порядка. К этому классу кривых относятся параболы, гиперболы, эллипсы, окружности, то есть все линии, уравнения которых содержат степени не выше второй. Кривая второго порядка не имеет точек перегиба. Прямые линии являются всего лишь частным случаем кривых второго порядка. Формула кривой второго порядка в общем виде может выглядеть, например, так:

x²+a₁y²+a₂xy+a₃x+a₄y+a₅=0. (6)

Таким образом, для описания кривой второго порядка достаточно пяти параметров.

 

Кривая третьего порядка. Отличие этих кривых от кривых второго порядка состоит в возможном наличии точки перегиба и особых точек (узловых или точек возврата первого рода). Например, график функции у = x ³ имеет точку перегиба в начале координат. Кривая у² = x³ имеет точку возврата первого рода в начале координат. Именно эта особенность позволяет сделать кривые третьего порядка основой отображения природных объектов в векторной графике. Например, линии изгиба человеческого тела весьма близки к кривым третьего порядка. Все кривые второго порядка, как и прямые, являются частными случаями кривых третьего порядка.

В общем случае уравнение кривой третьего порядка можно записать так:

x³ + a₁y³ + a₂x²y + a₃xy² + a₄x² + a₅y² + a₆xy + a₇x + a₈y + a₉=0. (7)

Следовательно, кривая третьего порядка описывается девятью параметрами.

Кривые Фергюсона и Безье. В 1963 году Фергюсон впервые ввёл кубическую параметризацию для определения кривых

r = r(t) = a₀ + a₁t + a₂t² + a₃t³. (8)

Для определения a₀, a₁, a₂, a₃ задают обычно значения r и dr/dt на обоих концах сегмента (рис. 5). Обозначая dr/dt через , получаем:

а₀ = r(0),

a₀ + a₁ + a₂ + a₃ = r(1),

a₁ = ,

a₁ + 2a₂ + 3a₃ = ,

отсюда

а₀ = r(0),

(9)

a₁ = ,

a₂ =3[ r(1) – r(0)] – 2 – ,

a₃ =2[ r(0) – r(1)] + + .

Подстановкой (9) в (8) можно выразить r через r(0), r(1), и

r = r(t) =r(0)(1– 3t² + 2t³) + r(1)(3t² – 2t³) + (t – 2t² + t³) + (– t² + t³). (10)

 

Рис. 5. Исходные данные для конструирования кривой по Фергюсону

В 1970 году Безье обобщил результаты Фергюсона (10) и предложил записывать параметрическое уравнение кривой в следующем виде

(11)

 

где r₀, r₁,… r_n – радиус-векторы (n+1)- вершин характеристической ломаной.

 

Полиномиальная кривая (11) проходит через точки Р₀ и Р_n, направления касательных в которых совпадают с направлениями векторов: Р₀Р₁ и Р_n-1Р_n.

Уравнения кривых Безье второго и третьего порядков могут быть записаны соответственно

r = r(t) = (1–t)² r₀ + 2t(1–t)r₁ + t²r₂,

r = r(t) = (1–t)³ r₀ + 3t(1–t)² r₁ + 3t²(1–t)r₂ +t³r₃.

Пример. Построить сегмент кривой Безье, представленной характерными точками Р₀(1,2), Р₁(3,4), Р₂(5,1).

Уравнение кривой в параметрическом виде будет записано

х(t) = (1–t)² + 6t(1–t) + 5t²,

y(t) = 2(1–t)² + 8t(1–t) + t². (12)

 

Вид этой кривой показан на рис. 6.

		0 1 2 3 4 5

 

Рис. 6. Пример построения кривой Безье второго порядка

 

Кубическая кривая в форме Безье проходит через точки r₀ и r₁, имеет касательную в точке r₀, идущую от r₀ к r₁, и касательную в точке r3,идущую от r2 к r3. Прямые Р₀Р₁, Р₁Р₂, Р₂Р₃ образуют характеристическую ломаную заданной кривой. Для построения кривой необходимо задать точки Р₀ и Р₃, затем на касательных к кривой в этих точках необходимо задать точки Р₁ и Р₂. Варьируя отрезками Р₀Р₁ и Р₂Р₃, можно изменять форму кривой (рис. 7).

Широкое применение кривых Безье в КГ объясняется простотой разработки соответствующих программ ЭВМ.

P0(r0)P3(r3)

Контур. Контур может быть как замкнутым, так и разомкнутым. Геометрические данные: начальная точка контура (х,у), дополнительные точки контура (x_i, y_i). Топологические данные: направление обхода, признак пересечения.

Векторный графический объект включает два элемента: контур и его внутреннюю область, которая может быть пустой или иметь заливку в виде цвета, цветового перехода (градиента) или мозаичного рисунка. В векторном объекте контур выполняет двойную функцию. Во-первых, с помощью контура можно менять форму объекта. Во-вторых, контур векторного объекта можно оформлять, предварительно задав его.

Многогранник. Каждая грань многогранника описывается уравнением

AX + bY + cZ + d = 0,

где x,y,z – отсчитываются в глобальной системе координат.

Многогранник описывается матрицей В

 

(13)

 

 

Поверхность. Если поверхность описана полиномиальной функцией, то коэффициенты уравнения хранятся в виде вектор-столбца.

При воспроизведении поверхностей средствами КГ объём необходимых ресурсов ЭВМ резко возрастает, поэтому локальные кусочно-непрерывные способы представления чаще всего являются единственно возможными.

Одним из решений можно рассматривать интерполяцию поверхности по методу С. Инаба, в котором заданы четыре точки и значения частных производных и в этих точках (рис. 8).

Уравнение отсека поверхности (рис. 8) в декартовых координатах, может быть записано в следующем виде:

 

(14)

Уравнение (14) имеет16 коэффициентов. Для их определения даны координаты четырёх точек и значение частных производных и в каждой точке. Каждый угол, таким образом, даёт по три параметра. Недостающие четыре параметра даёт задание координат четырёх точек, лежащих внутри поверхности.

 

 

 

 

 

 

В 1960 году Кунсом был разработан метод интерполяции поверхности по четырем граничным кривым (рис. 9):

 

	Рис. 9. Порция поверхности по Кунсу

 

 

T(u,u) = (1–u)×P(0, u) + u×P(1, u) + (1–u)×P(u, 0) + u×P(u, 1) – P(0,0)(1– u)(1 – u) – – P(0,1)(1–u)u – P(1,0)u (1–u) – P(1,1)uu.

 

Обобщая форму записи кривой Безье (11) для n = 3, получим уравнение поверхности:

,

(15)

 

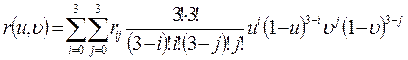
где – r _i,j вершины характеристического многоугольника (рис. 10).

 

 

r11 r21

r33

r23

r13

 

 

Объёмный примитив. В компьютерной графике под объёмными примитивами (элементарными геометрическими телами) понимают следующие тела: конус, цилиндр, сферу, параллелепипед, пирамиду, призму и т. д. Для того чтобы записать уравнение объёмного примитива, необходимо в уравнении поверхности вместо равенства перейти к неравенству. Например, уравнение

x² + y² + z² = R²

есть уравнение сферы, а неравенство

x² + y² + z² £ R²

задаёт объёмный примитив, также именуемый сферой.

Каждый объёмный примитив задаётся размерами формы в локальной системе координат. Например, цилиндр (рис. 11) имеет два размера формы: высоту H и диаметр основания D. Для требуемой ориентации отдельных примитивов применяют операции сдвига, переноса и вращения в пространстве. При этом описание примитива остаётся неизменным, изменяется лишь привязка его локальной системы координат к глобальной.

 

 

Рис. 11. Размеры формы объемного примитива

Синтез составных геометрических объектов (СГО) из объёмных примитивов выполняется с использованием геометрических операций, аналогичных операциям над множествами. Цель геометрического синтеза – получение описания сложного объекта. К операциям геометрического синтеза относятся: объединение, пересечение, разность, дополнение. На рис. 12 показаны примеры операций геометрического синтеза.

Для реализации этих операций используются методы контактного соединения и соединения с проникновением.

Метод контактного соединения используется для синтеза объектов из элементарных ГО, соединение которых осуществляется по плоским контурам. Примером контактного соединения будет объединение объектов, изображенное на рис. 12 б.

 

 

 

 

 

 

Метод соединения с проникновением предполагает следующую последовательность шагов:

а) определение объёмных примитивов V1 и V2;

б) определение пар потенциально пересекающихся поверхностей;

в) аналитическое определение кривой пересечения для любой пары пересекающихся поверхностей и удаление тех сегментов кривой, которые не лежат внутри пересекающихся поверхностей;

г) сегментация поверхностей в соответствии с полученной линией пересечения;

д) удаление сегментов поверхностей.

Структуры данных

Работа с большими объемами данных автоматизируется проще, если они упорядочены, то есть образуют определенную информационную модель. Информационную модель объекта получают, выделяя уровни структуризации данных и их взаимосвязь (рис. 13). Информационная модель зависит от реализуемой геометрической модели следующих уровней сложности: трёхмерная объёмная; трёхмерная полигональная; трёхмерная проволочная; двумерная полигональная; двумерная проволочная. Описание с помощью объемного трехмерного метода обеспечивает полное внутримашинное представление различных объектов.

С использованием трёхмерного полигонального описания рекомендуется создавать информационные модели тел с заданной толщиной.

С помощью двумерного полигонального описания можно описывать объекты с плоской формообразующей поверхностью и тела вращения. Основное же назначение двумерных методов – создание рисунков и чертежей.

Структура информационной модели зависит от класса прикладных задач, решаемых методами КГ. Например, информационная модель объектов, применяемых в деловой и иллюстративной графике, включает в себя элементы информационной модели 0, 1, 2, 3 – уровней. Информационная модель объектов, применяемых в САПР AutoCAD 2005, включает элементы уровней 0, 1, 2, 3, 4, 5 (рис. 13).

 

 

 

 

Рис. 13. Уровни структуризации данных

 

Существуют следующие виды моделей данных: реляционная, сетевая, списковая.

Реляционная модель данных – представление данных в виде таблиц. Отношения, включаемые в реляционную схему на основе информационной модели, можно подразделить на два класса: отношения, описывающие элементы этой структуры (тела, поверхности, линии и т. д.), и отношения, описывающие связи между этими элементами (принадлежность поверхностей телу, контуров поверхности и т. д.). В этой модели элементами являются строки или столбцы.

Преимущество реляционных моделей данных проявляется в возможности использования набора операций, основанных на теории множеств. К таким операциям относятся операции геометрического синтеза. Пример реляционной модели данных показан на рис. 14. Несмотря на отмеченные преимущества, практическое применение реляционных моделей в КГ находится ещё на начальном этапе.

 

 

	Отношения, описывающие элементы	Отношения, описывающие связи
RV (V, KENV) RF (F, KENF, DATE NF) RK (K, KENK, DATE NK)	R VF (V, F)   R FK (F, K)

Рис. 14. Использование реляционной модели данных

 

Сетевая модель данных. Модель можно представить в виде графа, вершины которого соответствуют поименованным группам записей, а ребра отражают смысловые связи. Основные понятия сетевой модели данных – запись и связь. Все записи, принадлежащие одному типу, объединяются в массив и упорядочиваются. Полная идентификация записи определяется именем массива (файла), типом записи и системным идентификатором. Между двумя типами записей можно установить множество типов связей (типов наборов). В наборе выделяют владельца набора и члена набора. В КГ простой пример записи – линия, которая является владельцем набора, а членами набора являются точки. Примером типа набора в этом случае будет иерархическая связь между двумя типами записей. Произвольный доступ ко всем элементам внутримашинного представления выполняется через определение сингулярных наборов, в котором владелец – сама система, а член – соответствующая запись. В сетевой модели над структурами можно выполнять операции, аналогичные операциям над множествами. Пример описания модели данных приведен на рис. 15.

 

 

	Запись	Набор	Отношения между элементами	Сингулярный набор
1: m 1: 1: n Точки Элементы набора Линии Система Владелец набора   Точки Отношения между точками и линиями и линиями Линии 1: n Линия Линия
К2 Кn К1 Система К2 P3 R2 P1 R4 R3 R2 R1 К1 P4 P3 P2 P1 К2 К1 К111 К2 Кn

Рис. 15. Пример сетевой модели данных

 

 

Список. Список – множество элементов данных (записей), между которыми при помощи указателей установлены взаимосвязи. Указатель – специальное поле в записи, указывающее местоположение другой записи, связанной с данной определённым отношением. Указатель может выражать машинный адрес, относительный адрес или идентификатор записи. Если записи расположены последовательно, то указатели не нужны. Примером списковой структуры данных в КГ является задание многоугольника списком вершин.

Преимущества векторной графики:

1. Изменение размера рисунка без потери качества. Векторные команды просто сообщают устройству вывода, что необходимо нарисовать объект заданного размера, использовав возможное количество точек. Другими словами, чем больше точек сможет использовать устройство вывода для создания объекта, тем лучше он будет выглядеть.

2. Можно редактировать отдельные части рисунка, не оказывая влияния на остальные.

3. Векторные изображения занимают относительно небольшое место в памяти компьютера.

Недостатком векторной графики является то, что она выглядит слишком искусственно.

Фрактальная графика

Фрактал — это фигура или часть фигуры, ко­торая может быть разбита на элементы, каждый из которых — уменьшенная копия целого.

Фрактальная графика отличается от векторной тем, что информация об геометрических объектах в памяти компьютера не хранится. Изображение строится по уравнению или системе уравнений, поэтому ничего, кроме формулы, хранить не надо.

Изменив коэффициенты в уравнении, можно получить совершенно другую картинку. При помощи этого способа можно строить простейшие регулярные структуры, а также сложные иллюстрации, которые имитируют ландшафты.

Фракталы бывают: геометрические, алгебраические и стохастические. Используя последние, получаются формы, похожие на природные.

Простой пример фрактала — так называемая "снежинка Коха" (рис. 16).

 

Рис. 16. Пример фрактала

Совсем другое дело — генераторы ландшафтов (landscape generators). На осно­вании сложных математических процедур они позволяют моделировать реальный мир. В отли­чие от большинства пакетов трехмерной графи­ки, генераторы ландшафтов оперируют поняти­ями, близкими к геодезии и метеорологии. Обла­ка, положение солнца, поверхность суши или гладь моря — вот составляющие, благодаря ко­торым строятся картины с помощью пакетов та­кого рода. Пользователь контролирует только время суток, рельеф местности или направление ветра, а программа сама воспроизводит обста­новку, которая сложилась бы в реальном мире при данных погодных условиях.

Базисом для та­ких пакетов являются фракталы, описанные уче­ным из исследовательского центра IBM Бенуа Мандельбротом. «Обла­ка — это не сферы, а береговая линия — не пря­мая». Это цитата из книги “Фрактальная геомет­рия природы” Мандельброта. Таким способом строят как простейшие регулярные структуры, так и сложные иллюстрации, имитирующие природные ландшафты и трехмерные объекты.

Когнитивная графика

Когнитивная графика — это совокупность приемов и методов образного представления условий задачи, которая позволяет либо сразу увидеть решение, либо получить подсказку для его нахождения. Когнитивная графика, таким образом, вновь возвращает исследователей к геометрическим методам решения задач, уже почти забытым из-за символьных вычислений.

Сравним две эти возможности, решая системы двух линейных алгебраических уравнений с двумя неизвестными. Пусть надо решить систему:

x+2y = 8,

Зх – 2y = 32.

Существуют два пути. Можно выразить х из первого уравнения, подставить второе, найти из него у, а затем вычислить х:

у = –1, х = 10.

Но можно воспользоваться алгебраическим способом, дающим для системы ax + by = с, dx + ey = f решение в виде:

x = (ce – bf)/(ae – bd),

y = (af – cd)/(ae – bd).

В любом случае, решая задачу, надо осуществлять подстановки и другие алгебраические преобразования, а также выполнять арифметические операции.

Если ввести систему координат и построить два графика, уравнениями которых являются выражения, входящие в систему, то решением системы будет точка пересечения двух прямых. Эти два подхода иллюстрируют достоинства и недостатки алгебраического и геометрического подходов.

Известный специалист в области искусственного интеллекта Д. А. Поспелов сформулировал три основных задачи когнитивной компьютерной графики:

· создание таких моделей представления знаний, в которых была бы возможность однообразными средствами представлять как объекты, характерные для логического мышления, так и образы-картины, которыми оперирует образное мышление;

· визуализация тех человеческих знаний, для которых пока невозможно подобрать текстовые описания;

· поиск путей перехода от наблюдаемых образов-картин к формулировке некоторой гипотезы о тех механизмах и процессах, которые скрыты за динамикой наблюдаемых картин.

Методы когнитивной графики используются в искусственном интеллекте в системах, способных превращать текстовые описания задач в их образные представления, и при генерации текстовых описаний картин, возникающих во входных и выходных блоках интеллектуальных систем, а также в человеко-машинных системах, предназначенных для решения сложных, плохо формализуемых задач.

Объемная (3D) графика

Трехмерная графика нашла широкое применение в таких областях, как: научные расчеты, инженерное проектирование, компьютерное моделирование физических объектов.

В инженерном проектировании используется твердотельное моделирование, где объекты представлены объемными примитивами, которые при объединении, вычитании и пересечении с другими объемными примитивами претерпевают необходимую трансформацию.

Компьютерное трехмерное моделирование объектов в анимации, играх предполагает выполнение следующих этапов:

· проектирование и создание виртуального каркаса («скелета») объекта, наиболее полно соответствующего его реальной форме;

· проектирование и создание виртуальных материалов, по физическим свойствам визуализации похожих на реальные;

· присвоение материалов различным частям поверхности объекта (на профессиональном жаргоне – «проецирование текстуры на объект»);

· настройка физических параметров пространства, в котором будет действовать объект, задание освещения, гравитации, свойств атмосферы, свойств взаимодействующих объектов и поверхностей;

· задание траектории движения объектов;

· расчет результирующей последовательности кадров;

· наложение поверхностных эффектов на итоговый анимационный ролик.

Для создания реалистичной модели объекта используют геометрические примитивы (прямоугольник, куб, шар, конус и прочие) и гладкие, так называемые сплайновые поверхности. В последнем случае применяют чаще всего метод бикубических рациональных В-сплайнов на неравномерной сетке (NURBS). Вид поверхности при этом определяется расположенной в пространстве сеткой опорных точек. Каждой точке присваивается коэффициент, величина которого определяет степень ее влияния на часть поверхности, проходящей вблизи точки. От взаимного расположения точек и величины коэффициентов зависит форма и «гладкость» поверхности в целом. Специальный инструментарий позволяет обрабатывать примитивы, составляющие объект, как единое целое, с учетом их взаимодействия на основе заданной геометрической модели.

Деформация объекта обеспечивается перемещением контрольных точек, расположенных вблизи. Каждая контрольная точка связана с близлежащими опорными точками, степень ее влияния на них определяется удаленностью.

Другой метод называют сеткой деформации. Вокруг объекта или его части размещается трехмерная сетка, перемещение любой точки которой вызывает упругую деформацию как самой сетки, так и окруженного объекта.

После формирования «скелета» объекта необходимо покрыть его поверхность материалами. Все многообразие свойств в компьютерном моделировании сводится к визуализации поверхности, то есть к расчету коэффициента прозрачности поверхности и угла преломления лучей света на границе материала и окружающего пространства. Для построения поверхностей материалов используют пять основных физических моделей:

· Boknight — поверхности с диффузным отражением без бликов (например, матовый пластик);

· Phong — поверхности со структурированными микронеровностями (например, металлические);

· Blinn — поверхности со специальным распределением микронеровностей с учетом взаимных перекрытий (например, глянец);

· Whitted — модель, позволяющая дополнительно учитывать поляризацию света;

· Hall — модель, позволяющая корректировать направления отражения и параметры преломления света.

Закраска поверхностей осуществляется методами Гуро (Gouraud) или Фонга (Phong). В первом случае цвет примитива рассчитывается лишь в его вершинах, а затем линейно интерполируется по поверхности. Во втором случае строится нормаль к объекту в целом, ее вектор интерполируется по поверхности составляющих примитивов, и освещение рассчитывается для каждой точки.

Свет, уходящий с поверхности в конкретной точке в сторону наблюдателя, представляет собой сумму компонентов, умноженных на коэффициент, связанный с материалом и цветом поверхности в данной точке. К таковым компонентам относятся:

· свет, пришедший с обратной стороны поверхности, то есть преломленный свет (Refracted);

· свет, равномерно рассеиваемый поверхностью (Diffuse);

· зеркально отраженный свет (Reflected);

· блики, то есть отраженный свет источников (Specular);

· собственное свечение поверхности (Self Illumination).

Свойства поверхности описываются в создаваемых массивах текстур (двух- или трехмерных). Таким образом, в массиве содержатся данные о степени прозрачности материала; коэффициенте преломления; коэффициентах смещения компонентов (их список указан выше); цвете в каждой точке, цвете блика, его ширине и резкости; цвете рассеянного (фонового) освещения; локальных отклонениях векторов от нормали (то есть учитывается шероховатость поверхности).

Следующим этапом является наложение («проектирование») текстур на определенные участки каркаса объекта. При этом необходимо учитывать их взаимное влияние на границах примитивов. Проектирование материалов на объект — задача трудно формализуемая, сродни художественному процессу и требует от исполнителя хотя бы минимальных творческих способностей.

Из всех параметров пространства, в котором действует создаваемый объект, с точки зрения визуализации самым важным является определение источников света. В трехмерной графике принято использовать виртуальные эквиваленты физических источников.

· Аналогом равномерного светового фона служит так называемый растворенный свет (Ambient Light). Он не имеет геометрических параметров и характеризуется только цветом и интенсивностью. Пример в природе — естественная освещенность вне видимости Солнца и Луны.

· Удаленный не точечный источник называют удаленным светом (Distant Light). Ему присваиваются конкретные геометрические параметры (координаты). Аналог в природе — Солнце.

· Точечный источник света (Point Light Source) равномерно испускает свет во всех направлениях и также имеет координаты. Аналог в технике — электрическая лампочка.

· Направленный источник света (Direct Light Souce) кроме местоположения характеризуется направлением светового потока, углами раствора полного конуса света и его наиболее яркого пятна. Аналог в технике — прожектор.

После завершения конструирования и визуализации объекта приступают к его «оживлению», то есть заданию параметров движения. Компьютерная анимация базируется на ключевых кадрах. В первом кадре объект выставляется в исходное положение. Через определенный промежуток задается новое положение объекта и так далее до конечного положения. Промежуточные значения вычисляет программа по специальному алгоритму. При этом происходит не просто линейная аппроксимация, а плавное изменение положения опорных точек объекта в соответствии с заданными условиями. В случае имитации живых объектов используют так называемые скелетные модели. То есть, создается некий каркас, подвижный в точках, характерных для моделируемого объекта. Движения точек просчитываются предыдущим методом. Затем на каркас накладывается оболочка, состоящая из смоделированных поверхностей, для которых каркас является набором контрольных точек, то есть создается каркасная модель. Каркасная модель визуализируется наложением поверхностных текстур с учетом условий освещения. В ходе перемещения объекта получается весьма правдоподобная имитация движений живых существ.

Наиболее совершенный метод анимации заключается в фиксации реальных движений физического объекта. В результате движения имитируемого объекта практически неотличимы от живого прототипа.

Процесс расчета реалистичных изображений называют рендерингом (визуализацией). Большинство современных программ рендеринга основаны на методе обратной трассировки лучей (Backway Ray Tracing). Его суть заключается в следующем.

o Из точки наблюдения сцены посылается в пространство виртуальный луч, по траектории которого изображение должно прийти в точку наблюдения.

o Для определения параметров приходящего луча все объекты сцены проверяются на пересечение с траекторией наблюдения. Если пересечения не происходит, считается, что луч попал в фон сцены и приходящая информация определяется только параметрами фона. Если траектория пересекается с объектом, то в точке соприкосновения рассчитывается свет, уходящий в точку наблюдения в соответствии с параметрами материала.

Сначала просчитывается преломленный и отраженный свет, затем проверяется видимость из точки пересечения всех источников света и интенсивность светового потока. Также вычисляются наличие, резкость и ширина бликов от каждого источника света.

Полученные итоговые значения цвета и интенсивности обрабатываются с учетом траектории луча и параметров атмосферы и присваиваются точке объекта как значения визуализации для наблюдателя. Затем процесс повторяется для всех элементов сцены. С целью упрощения расчетов пересечение проверяют не для каждой точки, а для примитива в целом.

Применение сложных математических моделей позволяет имитировать такие физические эффекты, как взрывы, дождь, огонь, дым, туман. Существуют методы расчета процедурных эффектов (Procedural Effects) и взаимодействия систем частиц (Partikle System). Однако их применение в полном объеме требует громадных вычислительных ресурсов, и потому в персональных компьютерах обычно используют упрощенные варианты. По завершении рендеринга компьютерную трехмерную анимацию используют либо как самостоятельный продукт, либо в качестве отдельных частей или кадров готового продукта.

Фильтрация изображения

Понятие фильтрации включает в себя любое преобразование графической информации. Фильтрация может быть задана не только в виде формулы, но и в виде алгоритма, его реализующего. Человек запоминает графическую информацию, в основном, в виде трех ее составляющих

1. Низкочастотные составляющие изображения. Они несут информацию о локализации объектов, составляющих изображение. Эта составляющая наиболее важна, так как связка «глаз – мозг» уделяет ей первостепенное внимание.

2. Высокочастотные составляющие изображения. Они отвечают за цветовые перепады – контуры изображения. Увеличивая их, мы повышаем резкость изображения.

3. Текстуры изображения. Текстуру можно трактовать как характеристику участков в контурах изображения.

 

Фильтры задают в виде квадратных матриц A (16):

. (16)

Пусть исходное изображение X, а получаемое как результат фильтрации – Y. Для простоты будем использовать матрицы 3 x 3:

(17)

Результат фильтрации Y формируется перемножением весовых множителей A с элементами изображения X.

Фильтром низких частот пользуются для подавления шума в изображении, чтобы сделать его менее резким. Высокочастотные фильтры используются для подчеркивания резкости изображения.