Если каждому значению действительной переменной 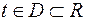 поставлен в соответствие вектор
поставлен в соответствие вектор  , то на множестве
, то на множестве  задана вектор-функция
задана вектор-функция  действительной переменной
действительной переменной  .
.
Задание вектор - функции  равносильно заданию трех числовых функций
равносильно заданию трех числовых функций 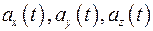 - координат вектора
- координат вектора  :
:
 ;
;

Производной вектор – функции  по аргументу
по аргументу  называется новая вектор – функция:
называется новая вектор – функция:

Если вектор  является радиус вектором точки
является радиус вектором точки  , то соответствующую вектор-функцию принято обозначать:
, то соответствующую вектор-функцию принято обозначать:
 .
.
Годографом вектор – функции  называется линия, описываемая в пространстве концом вектора
называется линия, описываемая в пространстве концом вектора  . Всякую линию в пространстве можно рассматривать как годограф некоторой вектор функции.
. Всякую линию в пространстве можно рассматривать как годограф некоторой вектор функции.
Параметрические уравнения годографа:
 .
.
Производные вектор – функции  имеют вид:
имеют вид:

Физический смысл производных:
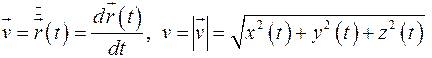 - вектор и величина скорости,
- вектор и величина скорости,
 - вектор и величина ускорения конца вектора
- вектор и величина ускорения конца вектора  , если
, если  - время.
- время.
Тангенциальная и нормальная составляющие ускорения равны:

Вектор  направлен по касательной к годографу вектор – функции
направлен по касательной к годографу вектор – функции  в сторону возрастания аргумента
в сторону возрастания аргумента  .
.
Уравнение касательной к пространственной кривой  в точке
в точке  , которой соответствует значение параметра
, которой соответствует значение параметра  , имеет вид:
, имеет вид:

где  текущие координаты касательной.
текущие координаты касательной.
Уравнение касательной к годографу вектор – функции 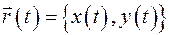 при
при 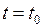 может быть получено из уравнения касательной к графику функции, заданной параметрически на плоскости:
может быть получено из уравнения касательной к графику функции, заданной параметрически на плоскости:

| № п/п | ЗАДАЧИ | Ответ |
| ПП13 III.№1. | Найти годограф вектор – функции  РЕШЕНИЕ:
Параметрические уравнения годографа:
РЕШЕНИЕ:
Параметрические уравнения годографа: 
 Исключая параметр
Исключая параметр  , получаем , получаем   Таким образом, годографом является окружность Таким образом, годографом является окружность  , ,  , из которой необходимо исключить точку , из которой необходимо исключить точку  , которая получается в пределе при , которая получается в пределе при  . .
|  , ,  , , 
|
| ПП13 III.№2. | Найдите годограф вектор – функции 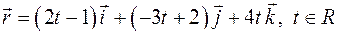 РЕШЕНИЕ:
Запишем координаты конца радиус – вектора:
РЕШЕНИЕ:
Запишем координаты конца радиус – вектора: 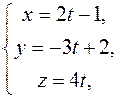 это параметрические уравнения прямой: это параметрические уравнения прямой:  . .
| Прямая

|
| ПП13 III.№3. | Найдите годограф вектор – функции 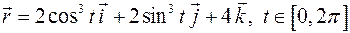 .
РЕШЕНИЕ: Запишем координаты конца радиус – вектора: .
РЕШЕНИЕ: Запишем координаты конца радиус – вектора: 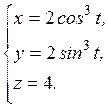 Кривая лежит в плоскости Кривая лежит в плоскости  , перейдем от параметрического представления кривой к ее виду в декартовых координатах, для чего возведем , перейдем от параметрического представления кривой к ее виду в декартовых координатах, для чего возведем  и и  в степень в степень  и сложим: и сложим: 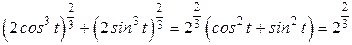 , или , или  . Это уравнение астроиды. . Это уравнение астроиды.
| Астроида 
|
| ПП13 III.№4. | Дано уравнение движения  .
Определите траекторию, скорость и ускорение движения. Постройте векторы и найдите скорости и ускорения для моментов .
Определите траекторию, скорость и ускорение движения. Постройте векторы и найдите скорости и ускорения для моментов  .
РЕШЕНИЕ: .
РЕШЕНИЕ:

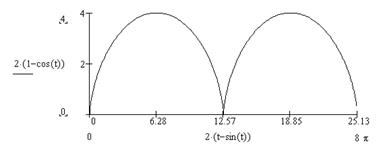
 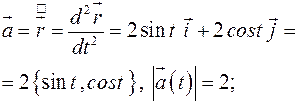
 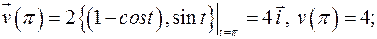


| Циклоида в
плоскости  : :

 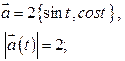




|
| ПП13 III.№5. | Найдите производную вектор – функции  РЕШЕНИЕ:
РЕШЕНИЕ:
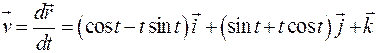 . .
| 
|
| ПП13 III.№6. | Найдите производную вектор – функции 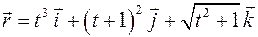 при при 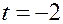 .
РЕШЕНИЕ: .
РЕШЕНИЕ:

| 
|
| ПП13 III.№7. | Найдите годограф вектор – функции  и напишите уравнение касательной к нему в точке, соответствующей и напишите уравнение касательной к нему в точке, соответствующей  .
РЕШЕНИЕ:
Параметрические уравнения годографа: .
РЕШЕНИЕ:
Параметрические уравнения годографа: 
 Используя свойство гиперболических функций
Используя свойство гиперболических функций 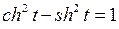 , получаем уравнение гиперболы , получаем уравнение гиперболы  в плоскости в плоскости  .
Таким образом, годографом является правая ветвь гиперболы, пробегаемая в направлении возрастания координаты .
Таким образом, годографом является правая ветвь гиперболы, пробегаемая в направлении возрастания координаты 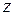 .
Уравнение касательной: .
Уравнение касательной: 
|  , ,
 ; ;
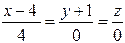 . .
|






