Для анализа спектра сигнала с угловой модуляцией, воспользуемся выражением (9.4), положив φο=0. Сигнал такого вида раскладывается в ряд Фурье по функциям Бесселя следующим образом
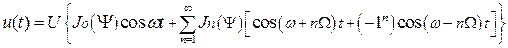(9.13)
Здесь Jn(Ψ) – функция Бесселя первого рода n – го порядка, аргументом которой является индекс модуляции Ψ.
Согласно (9.13), спектр сигнала с угловой модуляцией теоретически бесконечен. Форма огибающей спектра определяется зависимостью функций Бесселя от индекса модуляции. Графики первых четырёх функций Бесселя представлены на рисунке 9.2. Особенностью этих функций является затухающий колебательный характер, поэтому при некоторых значениях Ψ, указанных на рисунке 9.2, несущая частота (Jo) исчезает. В связи с этим, термин «несущая», при рассмотрении угловой модуляции, заменяют термином «средняя частота». Первый максимум функций Бесселя, начиная с n=1, соответствует Ψ=n+1.
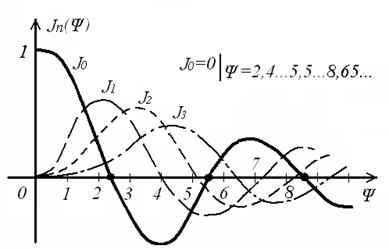
Рисунок 9.1 – Функции Бесселя
Затухающий характер функций Бесселя позволяет на практике без последствий ограничивать полосу занимаемых частот на уровне составляющих, амплитуда которых не превышает 1% от немодулированной несущей.
Эффективную полосу сигнала с угловой модуляцией в этом случае определяют эмпирической формулой
(9.14)
В последнем выражении Fмакс – максимальная частота модулирующего сигнала.
На рисунке 9.3 в качестве примера представлены спектры для некоторых значений Ψ [9].
Рисунок 9.3 – Спектры сигналов с угловой модуляцией.
Как уже отмечалось выше, при угловой модуляции одним гармоническим тоном, различия между ФМ и ЧМ нет, т.к индекс модуляции в этом случае величина постоянная. Иначе обстоит дело при модуляции сложным многочастотным сигналом. Поясним это на следующем примере. Пусть фазовая модуляция осуществляется двух тоновым сигналом, в котором одна частота (Ω1) очень низкая, а вторая (Ω2) во много раз выше первой. Поскольку при ФМ индекс модуляции не зависит от модулирующей частоты, спектры для обеих модулирующих частот будут подобны (см. рисунок 9.4а).
Предположим теперь, что при частотной модуляции на нижней частоте Ω1 индекс модуляции такой же, как при ФМ. Тогда на верхней частоте, согласно (9.11), индекс модуляции будет во много раз меньше, и, следовательно, эффективная полоса, при частоте модуляции Ω2, значительно сократится. Спектр сигнала с ЧМ для этого случая представлен на рисунке 9.4б.
Таким образом, при частотной модуляции реальным многочастотным сигналом, полоса модулированного сигнала (Пчм) оказывается значительно уже, по сравнению с полосой сигнала при фазовой модуляцией (Пфм). По этой причине, для целей радиосвязи и радиовещания предпочтение отдаётся частотной модуляции.
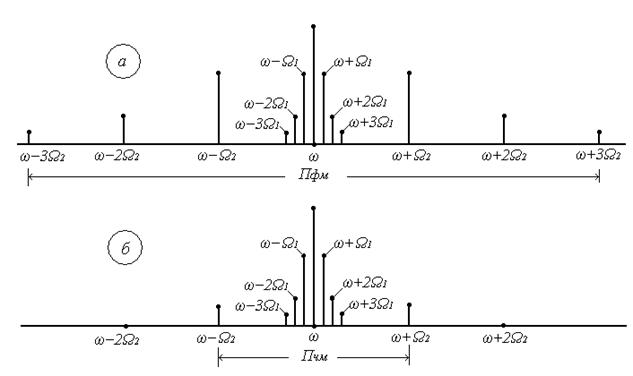
Рисунок 9.4 – Спектры сигналов с ФМ и ЧМ
