Индекс жизненности Iv (индекс Покровского), в отличие от естественного прироста, представляет собой не разность, а отношение числа родившихся N к числу умерших M, умноженное для легкости интерпретации на сто: 
. И показатели естественного прироста, и индекс жизненности измеряют скорость «естественного движения» населения и являются общими характеристиками замещения поколений. В качестве колич характеристики естественного движения населения также используется истинный коэф-т естественного прироста населения r. Его преимущество по сравнению с наблюдаемыми коэф-ми естественного прироста состоит в том, что в отличие от них он свободен от влияния возрастной структуры. На основе истинного коэф-та можно выделить: если r > 0, то это означает, что при сохранении заданных возрастных интенсивностях рождаемости и смертности численность населения страны имеет тенденцию к увеличению, т.е. в данном случае речь идет о расширенном воспроизводстве. Если r = 0, то мы имеем дело с населением, в котором родительские поколения замещаются равными им по численности детскими поколениями. Численность такого населения при сохранении зафиксированных режимов рождаемости и смертности в перспективе изменяться не будет. Данный режим воспроизводства называется простым. Если режимы рождаемости и смертности задают стабильное население, численность которого сокращается, т.е. r < 0, то такой тип воспроизводства называют суженным. Приближенное значение истинного коэффициента естественного прироста рассчитывалось по формуле 
, где знаменатель определялся значением среднего возраста матери при рождении детей.
С точки зрения техники расчетов брутто-коэффициент воспроизводства населения (принятые обозначения R или GRR) - частный случай суммарного коэффициента рождаемости. Расчеты брутто-коэффициента выполняются по приближенной формуле: 
. Здесь δ —доля девочек среди новорожденных (примерно равна 0,488 и одинакова для всех возрастов женщин). Суммарный коэффициент рождаемости равен: 
, где Nx — число зарегистрированных рождений в течение года у матерей в возрасте x, 
— среднегодовая численность женщин данного возраста, α и β представляют границы репродуктивного интервала (обычно α = 15, β = 50 лет). Однако в интерпретации этих двух показателей имеется значимое различие. Суммарный коэффициент рождаемости — это число рождений детей обоих полов, которое может иметь женщина при сохранении наблюдаемых уровней повозрастной рождаемости. Брутто-коэффициент воспроизводства (для гипотетического поколения) - среднее число девочек, которое может родить одна женщина, при условии дожития до конца репродуктивного периода и сохранения на его протяжении современных уровней рождаемости в каждом возрасте. Недостаток: фактически при его расчете делается допущение, что все дочери доживают до конца репродуктивного периода.
Нетто-коэффициент воспроизводства населения (принятые обозначения R0 или NRR) - среднее число девочек, рожденных за всю жизнь одной женщиной, дожившей до конца репродуктивного периода при данных уровнях рождаемости и смертности. Фактически он измеряет скорость замещения материнского поколения дочерним. Расчеты R0 выполняются по формуле: 
, где 
- возрастной коэффициент рождаемости в возрасте x, 
- среднее число живущих женщин в возрасте x по таблице смертности, l0 =100000 — корень таблицы смертности. Нетто-коэффициент воспроизводства с хорошей степенью точности можно вычислять и по упрощенной формуле R0 = l(x)*ΣF(x), что равносильно R0 = R*l(x), где l(x) — число женщин, доживающих до среднего возраста матери x при рождении детей. В стабильном населении, как уже отмечалось выше, R0 соотношением R 0= erT связан с истинным коэф-ом естественного прироста населения r. В случае расширенного вос-ва, когда r > 0, то R0 > 1, т.е. дочернее поколение многочисленнее материнского. В случае суженного вос-ва из r < 0 вытекает R0 < 1, т.е. дочернее поколение не замещает материнского. При простом вос-ве, когда r = 0, нетто коэф-т будет равен 1, а численности дочерей и матерей будут совпадать.
Для оценки экономичности режимов воспроизводства населения используется показатель «цена простого воспроизводства». Он показывает, сколько девочек в среднем необходимо родить женщине, чтобы обеспечить простую замену материнского поколения: ρ = R / R0. Чем выше цена простого воспроизводства, тем ниже экономичность воспроизводства, и наоборот. Высокая цена простого воспроизводства является результатом высокой смертности.
41. Модель стабильного населения. Применение модели стабильного населения.
Модель стабильного населения - теоретическое закрытое население с неизменными во времени возрастными интенсивностями рождаемости, смертности и возрастной структурой населения. Модель стабильного населения является упрощенным изображением процесса воспроизводства населения. Она строится для одного, главным образом для женского пола. Леонард Эйлер (1760).
Асимптотически стабильное население - закрытое население, в котором возрастные интенсивности рождаемости и смертности с определенного момента времени стали постоянными, со временем будет иметь неизменную возрастную структуру, постоянные общие коэффициенты рождаемости и смертности и коэффициент естественного прироста. (Лотка и Ф.Шарп). Процесс приближения его первоначальной возрастной структуры и общих демографических коэффициентов к некоторым постоянным (предельным) значениям — стабилизацией населения. В процессе стабилизации возрастная структура населения постепенно как бы «забывает» свою первоначальную форму. Это особое свойство получило название сильной эргодичности. После того, как население достигнет стабильного состояния, параметры его возрастной структуры будут определяться только заданными режимами рождаемости и смертности. Когда уровни рождаемости и смертности непрерывно изменяются, так же непрерывно изменяется возрастная структура населения. С каждым годом влияние исходной возрастной структуры на форму каждой последующей ослабевает и постепенно сходит на «нет». Это свойство любого населения с изменяющимися параметрами рождаемости и смертности удаляться от своей возрастной структуры далекого прошлого получило название слабой эргодичности.
Теорема Лопеса: если два населения подчиняются одинаковым, но изменяющимся во времени режимам рождаемости и смертности, то эти два населения, в конце концов, приобретут одинаковые возрастные структуры, хотя конечно эти структуры не обязательно стремятся к пределу, как в случае стабильного населения.
1. Общие коэффициенты рождаемости и смертности стабильного населения постоянны. Общие коэффициенты рождаемости n и смертности m можно выразить формулами 
и 
, где f x и mx — соответственно, возрастные коэффициенты рождаемости, а cx —доля лиц в возрасте от x до x +1 лет.
2. Коэффициент естественного прироста стабильного населения постоянен. r=n-m, где r - коэффициента естественного прироста.
3. Стабильное население растет по экспоненциальному закону (или в геометрической прогрессии). Численность населения изменяется по этим законам, если его коэффициент прироста неизменен во времени: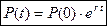 
4. Число родившихся и умерших в стабильном населении изменяются по экспоненциальному закону (или в геометрической прогрессии).
Доля возрастной группы x в общей численности стабильного населения определяется по формуле 
. Общий коэффициент рождаемости равен n=c(0). Для расчетов функции возрастной структуры c(x): 
, где x+τ/2 - середина возрастного интервала.
Возрастная структура зависит от двух переменных: порядка вымирания l(x) и одного из двух взаимосвязанных коэффициентов — общего коэффициента рождаемости и коэффициента естественного прироста. При этом, чем выше, при прочих равных условия,коэффициент естественного прироста или общий коэффициент рождаемости, тем ниже доля лиц старших возрастов в общей численности населения.
У модели стабильного населения имеется одно фундаментальное свойство, которое объясняет ее мощные аналитические возможности. Оно заключается в том, что каждой комбинации возрастных распределений смертности l(x) и рождаемости f (x) соответствует единственное стабильное население с определенной возрастной структурой, общими коэффициентами рождаемости и смертности, а также коэффициентом естественного прироста. Общие коэффициенты рождаемости и смертности, коэффициент естественного прироста стабильного населения свободны от влияния возрастной структуры. Поэтому с их помощью, освободившись от влияния значимого структурного фактора, можно лучше понять демографическую специфику данного периода. По этой причине коэффициенты стабильного населения назвали истинными коэффициентами соответственно рождаемости, смертности и естественного прироста.
Модель стабильного населения широко используется в аналитических целях. В ее терминах определяются многие демографические индикаторы, в первую очередь система показателей режима воспроизводства.
На практике для оценки сложившейся демографической ситуации широко используется метод сравнения параметров реального и стабильного населения. С помощью модели стабильного населения исследуются разнообразные теоретические проблемы, изучение которых на основе наблюдений за реальными данными затруднено. В первую очередь это относится к изучению взаимосвязей между возрастной структурой и процессами смертности и рождаемости. Включение в модель миграции позволяет узнать, каким образом миграционные процессы влияют на процесс воспроизводства населения. На основе модели стабильного населения разработаны методы получения, восстановления или коррекции информации в условиях неполных или недостоверных данных.
42. Модель стационарного населения.
Cтационарное население — это теоретическое население с неизменными числами рождений и возрастными характеристиками смертности, определяемыми таблицей смертности.
Возрастные коэффициенты смертности стационарного населения определяются соответствующей функцией m(x) таблиц смертности. Возрастная структура стационарного населения задается табличной функцией L(x). В таблицах смертности L(x) обозначает число человеко-лет, прожитых в интервале теми, кто достиг возраста x. В модели стационарного населения этот показатель определяет численность соответствующей возрастной группы. Поэтому второе название L(x) — число живущих в стационарном населении в возрасте x.
Поскольку функция L(x), как и другие функции таблиц смертности, по условиям построения модели неизменна, постольку постоянной является и возрастная структура стационарного населения. Общая численность стационарного населения соответственно равна сумме всех L(x), т.е. 
. Здесь ω — предельный возраст таблиц смертности. Аналог этого показателя в таблицах смертности T(0) интерпретируется как общее число человеко-лет, которое проживут все новорожденные. Доля отдельной возрастной группы в общей численности стационарного населения составляет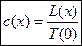 
. Число умерших в отдельных возрастных группах стационарного населения выражается функцией d(x). Общее число родившихся в течение года в стационарном населении равно корню таблицы смертности l(0). Общий коэффициент смертности в стационарном населении равен 
; общий коэффициент рождаемости равен 
.
Свойства стац населения: 1) из равенства числа умерших числу родившихся, т.е.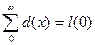 
, следует: а) естественный прирост стационарного населения равен нулю; б) общие коэффициенты рождаемости и смертности в стационарном населении равны: m = n; в) (с учетом условия закрытости) общая численность стационарного населения неизменна во времени. 2) общие коэффициенты смертности и рождаемости обратно пропорциональны ожидаемой продолжительности предстоящей жизни при рождении. Из определения ожидаемой продолжительности предстоящей жизни при рождении 
и определений общих коэффициентов (см. свойство 3) следует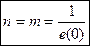 
. 3) постоянство всех демографических показателей обусловливает идентичность всех возрастных характеристик реального и условного поколений в стационарном населении, что хорошо видно на сетке Лексиса.
4) численность поколений в стационарном населении равна числу родившихся, умноженному на среднюю продолжительность предстоящей жизни при рождении, т.е. 
. 5) средний возраст умерших стационарного населения равен ожидаемой продолжительности предстоящей жизни при рождении.
В дем исслед модель стац нас является одним из средств сравнит анализа дем процессов и структур. Так, возр структ стац нас применяется в качестве стандарта для сравнения смертности методом стандартизации. Модель стац нас применяется для изучения дем хар-к реал нас. Очевидно, что в действ-ти не бывает нас, колич-ые хар-ки кот бы полностью совпадали с пар-ми стац модели. Под «нас.» можно понимать не только численность людей, прожив на опред тер-рии, но и чис-ть персонала на предприятиях, учащихся школ и вузов, клиентов страх компаний и пенсионных фондов, пациентов больниц и др. В целом, совок-ти, для кот можно построить модель стац нас (или табл смертн) обладают одним общим св-ом. Выбытие элемента из сов-ти, подобно смерти, представляет собой неповтор событие, интенсивность кот зависит от возраста элемента.
43. Классификация демографических прогнозов. Методы разработки гипотез прогноза.
Прогнозы населения — научно обоснованная информация о будущих тенденциях изменения численности, параметров воспроизводства и структур населения на местном (региональном), национальном и глобальном уровнях.
Разнообразие задач, решаемых с помощью прогнозов населения, обусловливает существование многих видов таких прогнозов. Наибольшее значение имеют классификации прогнозов населения по их назначению, по длине периода прогнозирования, по количеству объектов прогнозирования, по типу представления прогнозируемой величины и по методу построения.
По назначению: 1) реалистические (прогнозируемые величины близки к действительности), 2) аналитические (прогнозируемые величины отражают результаты каких-либо действий — например, преодоления смертности от какой-либо причины) и 3) прогнозы-предостережения (прогнозируемые величины характеризуют перспективы, которых следует избегать).
По длине периода прогнозирования: 1) краткосрочные (до 5 лет), 2) среднесрочные (на 5–20 лет) и 3) долгосрочные (на 20–50 лет) прогнозы.
По количеству объектов прогнозирования: 1) единичные (изменения одной переменной) и 2) множественные (изменения двух или более переменных) прогнозы.
По типу представления прогнозируемой величины: 1) точечными (величина представлена одним числом) или
2) интервальными (величина представляется в интервале показателей или в виде различных вариантов).
По методу построения: 1) математическим методом (прогнозируемая величина описывается единой функцией от своего базового значения и переменной времени), 2)методом компонент (прогнозируемая величина является результатом изменений ее составляющих, описываемых различными функциями) и 3)казуальным методом (прогнозируемая величина является зависимой переменной в эконометрическом уравнении, связывающем эту величину с ее социально-экономическими детерминантами).
Любой прогноз населения строится по определенной процедуре, включающей следующие: 1) выбор прогнозной модели, описывающей будущее изменение населения (сценарий изменения показателей воспроизводства населения); 2) определение параметров выбранной прогнозной модели; 3) применение выбранной прогнозной модели к исходным фактическим показателям.
Способы разработки гипотезы: 1) прогноз на основе исторических аналогий — основывается на сопоставлении тенденций воспроизводства населения в стране, для которой строится прогноз, и стране, опережающей первую в демографическом развитии (например, в долгосрочной перспективе развивающимся странам предстоят изменения демографических процессов, аналогичные происходящим в настоящее время в экономически развитых странах). 2) трендовый прогноз - в основе ежит экстраполяция выявленных тенденций. (Проблемы: 1.прогнозист, как правило, не допускает неопределенно долгое сохранение в будущем тех тенденций, которые в исходный период имеют негативный характер (например, рост смертности от какой-либо причины). Решение: определить период допустимости трендового прогноза. 2.простая экстраполяция существующих тенденций (например, снижения показателей смертности) технически может привести к тому, что вероятность смерти окажется отрицательной, что противоречит здравому смыслу. Решение: ввести дополнительные ограничения). 3) прогноз на основе суммарных характеристик. Например, на основе показателя ожидаемой продолжительности жизни и типовых таблиц смертности прогнозируются возрастные коэффициенты смертности. 4) нормативный прогноз — предполагает изменение показателей воспроизводства населения в результате каких-либо усилий общества. Например, уровень смертности в каком-либо возрасте может снижаться вследствие полной или частичной элиминации смертности от отдельной причины. 5) прогноз на основе экспертных оценок — учитывает мнение специалистов (причем в самых широких областях науки) о наиболее вероятных тенденциях изменения демографических процессов в будущем. Данный метод предполагает тщательный отбор экспертов, разработку специальных анкет для их опроса и методики обработки полученных данных.
При построении прогнозов используются два вида данных: исходные демографические показатели (фактические данные, служащие базой для построения прогноза) и параметры модели (описывающие предстоящие изменения населения). Определение параметров модели — наиболее сложная проблема в рамках построения прогноза, так как нет возможности наверняка утверждать, какие изменения ожидают население в будущем.
44. Когортно-компонентный метод прогноза возрастно-половой структуры населения. здесь никак не сократить
Метод компонент (когортно-компонентный) рассматривает динамику численности населения как результат изменения ее составляющих — чисел рождений, смертей, чистого числа мигрантов, — каждая из которых прогнозируется по отдельности.
Допустим, нам предстоит построить методом компонент прогноз численности мужского населения в возрастной группе х+ 1 лет на 1 января t+ 1 года (Pm,x+1,t+1) в стране, где отсутствует внешняя миграция. При прогнозировании мы можем использовать данные о численности мужского населения по возрастам и показатели таблицы смертности мужского населения за предыдущий год. Обратимся к сетке Лексиса Речь идет о вертикальном отрезке CD. В то же время отрезок CD лежит на пересечении горизонтальной полосы х +1 исполнившихся лет и диагональной полосе включающей линии жизни людей, которые родились в t –3 году. Таким образом, прогнозируемая численность населения состоит из людей, которые 1 января года t находились в возрасте х полных лет и объединялись отрезком AB. Эта численность населения (обозначим ее Pm,x,t) и послужит нам базой для прогноза. Очевидно, прогнозируемая численность населения Pm,x+ 1 ,t+ 1 отличается от базовой численности населения Pm,x,t, поскольку некоторая ее часть не доживет до 1 января t +1 года. Строго говоря, прогнозируемая и базовая численности населения связаны следующим уравнением: Pm , x +1, t +1 = Pm , x , t (1− qm , x +1/ 2, t), где qm,x+ 1/2, t — вероятность того, живой мужчина, достигший точного возраста х +1/2 лет в середине года t, не доживет до середины года t+ 1 (линия жизни такого мужчины прервется на отрезке, ограниченном точками Y и Z). Выражение (1− qm , x +1/ 2, t) используется в уравнении, так как средний возраст в совокупности людей, которым в предыдущий день рождения исполнилось х полных лет (то есть в базовой численности населения), составляет х +1/2 года. Поскольку точка Z принадлежит t +1 году, данными за который мы не располагаем на момент построения прогноза, постольку выражение 1− qm , x +1/ 2, t мы заменяем на приблизительно равное: Pm , x +1, t +1 ≈ Pm , x , t (Lm , x +1, t / Lm , x , t), где Lm,x+ 1, t, Lm,x,t — соответственно, числа живущих в возрастах х+ 1 и х лет, рассчитанные для мужского населения в году t (этим числам соответствуют отрезки GH и EF). Соотношение (Lm, x +1, t / Lm, x, t) получило название коэффициента передвижки, а процедура, применяющая данное соотношение, — метода передвижки возрастов.
Для прогноза численности мужского населения в возрасте 0 лет в году t +1 (Pm ,0, t +1) используется следующая формула: Pm , 0, t +1 = Nm , t (1−1/ 2 qm ,0, t) (видимо в учебнике опечатка, но я не знаю как исправить!), где Nm,t — число мальчиков, родившихся в период от середины года t до середины года t +1, 1/ 2 qm ,0, t — вероятность того, что мальчик, родившийся между серединой года t и серединой года t +1, не доживет до середины года t +1.
Выражение (1−1/ 2 qm ,0, t) используется в уравнении, так как средний возраст людей, которым в середине года t +1 было меньше 1 года, составляет 1/2 года. Аналогично, заменим правую часть уравнения на приблизительно равную: Pm , 0, t +1 = Nm , t (Lm ,0, t / lm ,0, t), где Lm,0,t — число живущих в возрасте 0 лет, рассчитанное для мужского населения в году t; lm,0,t – корень таблицы смертности, рассчитанной для мужского населения в году t.
Чтобы рассчитать величину Nm,t, необходимы данные об общих числах родившихся в годы t и t+ 1:
, где Nt– 1/2 и Nt +1/2 — числа родившихся в календарные годы t и t +1 (символы t –1/2 и t +1/2 обозначают, что учитываемые рождения произошли, соответственно, до середины года t и после середины года t +1); δ m — доля мальчиков в общем числе родившихся; fx,t –1/2 и fx,t +1/2 — возрастные коэффициенты рождаемости в календарные годы t и t +1; Pf,x,t и Pf,x,t +1 — численности женского населения в возрасте х в годы t и t +1, соответственно.
Исходя из того, что возрастные коэффициенты рождаемости за один календарный год изменяются мало, уравнение можно записать: Nm , t ≈ δ m Σ f x , t (Pf , x , t + Pf , x , t +1) / 2. Если учесть влияние миграции, то прогнозируемые численности населения составят: Pm,x+ 1 ,t +1 ≈ Pm,x,t (Lm,x+ 1, t / Lm,x,t) + MIGRm,x +1, t +1, Pm, 0 ,t +1 ≈ Nm,t (Lm, 0, t / lm ,0 ,t) + MIGRm, 0, t +1, где MIGRm,x+ 1, t +1, MIGRm, 0, t +1 — сальдо миграции мужского населения, пережившего середину t +1 года в возрасте х +1 и 0 лет, соответственно, за период с середины года t до середины года t +1.
На практике значительно чаще используется другой способ — с применением более широких возрастных групп. При этом все возрастные группы (кроме наиболее старшей) должны быть одинаковой «ширины», а срок прогнозирования за одну итерацию должен быть равен «ширине» возрастных групп: nPm,x+n,t+n = nPm,x,t (nLm,x+n,t/ / nLm,x,t) + n MIGR m,x+n,t+n, nPm,0,t+n = nNm,t (nLm,0,t / nlm,0,t) + n MIGR m,0,t+n, nNt = n Σn fx,t (nPf,x,t + nPf,x,t+n) / 2, где n — ширина используемых возрастных групп и срок прогнозирования за одну итерацию; nLm,x+n,t и nLm,x,t — числа живущих в возрастах х и х+n лет; nPm,x,t — численность мужского населения в возрасте от х до х+n лет в середине года t; nMIGRm,x+n,t+n — сальдо миграции мужского населения, пережившего середину года t+n в возрасте от х до х+n лет, за период с середины года t до середины года t+n; nNt — число родившихся за период с середины года t до середины года t+n; n fx,t — возрастной коэффициент рождаемости в группе от х до x+n лет за период с середины года t до середины года t+n. Смысл последних уравнений состоит в том, что при отсутствии внешней миграции разность между численностью населения в возрасте х лет и старше в году t и численностью населения в возрасте х+n лет и старше в году t+n равна числу смертей, произошедших за период с года t до года t+n среди лиц, которым в году t исполнилось х и более лет. Чтобы определить общее число смертей за указанный период, необходимо дополнительно учесть смертность детей, родившихся за период с t до t+n года.
Прогноз на срок, продолжительность которого отличается от величины кратной «ширине» используемых возрастных групп (например, на срок 12 лет при 5-летних возрастных группах), может быть получен интерполяцией прогнозов на стандартные сроки (в указанном случае — на сроки 10 и 15 лет). Такая интерполяция может быть произведена с помощью какой-либо из математических моделей (линейного, геометрического или экспоненциального роста).
Основное преимущество метода компонент (когортно-компонентного метода) заключается в возможности прогнозирования возрастно-половой структуры населения. Перспективные
оценки возрастно-половой структуры населения служат основой для функциональных прогнозов населения.
45. Роль ООН в решении актуальных демографических проблем современного мира. все из инета
Основные направления деятельности ООН в области народонаселения:
- сбор, обработка и распространение демографической информации;
- разработка рекомендаций для международного сообщества и государств — членов ООН по реализации мер демографической политики;
- исследование проблем народонаселения, включая анализ взаимодействия демографических, социальных, экологических и экономических процессов;
- организация и проведение под эгидой ООН международных конференций по народонаселению на межправительственном уровне.
С 1946 года до середины 1960-х годов ведущими направлениями деятельности ООН в области народонаселения были проблемы учёта и статистики населения. При техническом содействии ООН в рамках переписей населения они были проведены во многих развивающихся странах, осуществлена унификация программ ряда национальных переписей. После 1970-1980-е вопросы учёта и использования демографических факторов в демографических мероприятиях экономической и социальной политики и международного сотрудничества в сфере экологии. С целью решения демографической проблемы ООН приняла «Всемирный план действия в области НН» (важное место уделялось планированию семьи).
В структуру вспомогательных органов Экономического и Социального Совета ООН входит Комиссия по народонаселению и развитию.
ООН издаётся много специализированной демографической литературы: демографический ежегодник ООН, «Новости народонаселения» и т. д.
