По определению f=n!=1 ∙ 2 ∙ …∙ (n-1) ∙ n (при n≥1) и f=0!=1 (при n=0).
Таким образом, вычисление факториала сводится к задаче вычисления произведения значений целых чисел, изменяющихся от 1 до n с шагом 1.
Накопление произведения будем производить по рекуррентной формуле: fi = fi-1 ∙ i;  ; f0 = 1.
; f0 = 1.
Схема алгоритма и код программы приведены на рис. 4.5.2-13
| Function Pr52-13(ByVal n As Integer) As Long Dim f As Long Dim i As Integer f = 1 For i = 2 To n f = f * i Next i Return f End Function |
Рис. 4.5.2-13. Схема алгоритма и программный код процедуры Pr5213() Примера 4.5.2-4
| Dim nn As Integer Dim ff As Long Nn = vvodInt4(TextBox1) ff = Pr5213(nn) vivodLngFx7(ff, TextBox2) |
Рис. 4.5.2-14. Пример вызова процедуры Pr5213()
Процедура – функция Pr5213() может быть вызвана, например, как показано на рис. 4.5.2-14.
Пример 4.5.2-5. Написать процедуру-подпрограмму, которая находит наименьшее значение функции y=c∙e-dx∙sin(2x+5), где c, d – входные параметры, а x изменяется на отрезке [a; b] с шагом h.
Схема алгоритма и код программы приведены на рис. 4.5.2-15.
Алгоритм нахождения наименьшего (наибольшего) значения функции основан на последовательном сравнении очередного значения функции с текущим наименьшим (наибольшим) значением функции. В качестве начального наименьшего значения ymin следует использовать число, близкое к наибольшему числу из диапазона возможных значений того типа данных, который описывает рассматриваемую функцию, чтобы наверняка выполнилось условие y < ymin при первом проходе цикла. То есть, за ymin можно принять число, близкое к наибольшему из диапазона значений данных типа Doublе, т.е Double.MaxValue.
| Sub Pr5215(ByVal n As Integer, _ ByVal a As Double, _ ByVal c As Double, _ ByVal d As Double, _ ByVal h As Double, _ ByRef xmin As Double, _ ByRef ymin As Double) Dim i As Integer Dim x, y As Double ymin = Double.MaxValue x=a For i =1 To n y =c*Exp(-d*x)*Sin(2*x+5) If y<ymin Then ymin=y: xmin=x End If x =x+h Next i End Sub |
Рис. 4.5.2-15. Схема алгоритма и программный код процедуры Pr5215() Примера 4.5.2-5
Соответственно, за начальное значение ymax можно принять число
Double.MinValue, т.е. число, близкое к наименьшему числу из диапазона значений Double, для того чтобы при первом проходе цикла гарантированно выполнялось условие y > ymax. Для определения значения аргумента xmin (xmax), соответствующего найденному наименьшему (наибольшему) значению функции при каждом переопределении текущего наименьшего (наибольшего) значения функции надо одновременно переопределять текущее значение xmin (xmax).
Процедура – функция Pr5215() может быть вызвана из любой другой процедуры или из модуля формы, например, как показано на рис. 4.5.2-16.
| Dim nn As Integer Dim aa, bb, hh, cc, dd, ym, xm As Double aa = vvodDbl2("Введите значение a=",TextBox1) bb = vvodDbl2("Введите значение b=",TextBox2) hh = vvodDbl2("Введите значение h=",TextBox3) cc = vvodDbl2("Введите значение c=",TextBox4) dd = vvodDbl2("Введите значение d=",TextBox5) nn = CInt((bb-aa)/hh)+1 Pr5215(nn, aa, cc, dd, hh,xm, ym) vivodDblFx6(xm, TextBox6) vivodDblFx6(ym, TextBox7) |
Рис. 4.5.2-16. Пример вызова процедуры Pr5215()
Пример 4.5.2-7. Получить таблицу значений функции z(x,y)=x2+y2 в заданных диапазонах значений аргументов  , если шаг изменения x равен hx, а шаг изменения y равен hy.
, если шаг изменения x равен hx, а шаг изменения y равен hy.
Схема алгоритма и код программы приведены на рис. 4.5.2-17.
| Sub Pr5217(ByVal n As Integer, _ ByVal m As Integer, _ ByVal a As Double, _ ByVal hx As Double, _ ByVal c As Double, _ ByVal hy As Double) Dim x, y, z As Double Dim j, i As Integer x = a For i = 1 To n y =c For j = 1 To m z = x^2 + y^2 vivodDblFx6(x, TextBox7) vivodDblFx6(y, TextBox8) vivodDblFx6(z, TextBox9) y = y + hy Next j x = x + hx Next i End Sub |
Рис. 4.5.2-17. Схема алгоритма и программный код процедуры Pr5217() Примера 4.5.2-7
Процедура Pr5217() может быть вызвана из любой другой процедуры или из модуля формы, например, как показано на рис. 4.5.2-18.
| Dim nn, mm As Integer Dim a, b, hx, c, d, hy As Double a = vvodDbl2("Введите значение a", TextBox1) b = vvodDbl2("Введите значение b", TextBox2) hx = vvodDbl2("Введите значение hx",TextBox3) c = vvodDbl2("Введите значение c", TextBox4) d = vvodDbl2("Введите значение d", TextBox5) hy = vvodDbl2("Введите значение hy",TextBox6) nn = CInt((b-a)/ hx) + 1 mm = CInt((d-c) / hy) + 1 Sub Pr5217(nn, mm, a, hx, c, hy) |
Рис. 4.5.2-18. Пример вызова процедуры Pr5217()
Пример 4.5.2-8. Создать проект Пример 4.5.2-8, который выводит в текстовое окно значения функции y=  +cosx3 на отрезке [a; b] с шагом h.
+cosx3 на отрезке [a; b] с шагом h.
Форма должна содержать три элемента Label для записи подсказок вводимых переменных и три текстовых поля TextBox для ввода значений этих переменных. На форме должно быть также текстовое поле для вывода значений функции и аргумента. Для этого текстового поля необходимо задать свойство MultiLine, равное True, а свойство ScrollBars– в значении Vertical для возможности прокрутки текстового поля по вертикали. Помимо этого, на форме должна быть кнопка Button1, с которой необходимо связать программный код.
Форма должна быть такой, как на рис. 4.5.2-19.
Результаты работы проекта представлены на рис. 4.5.2-19.
Программный код проекта приведен рис. 4.5.2-20.
Рис. 4.5.2-19. Форма проекта Пример 45.2-8 с результатами
| Option Explicit On Option Strict On Imports System.Math Public Class Form1 Function vvodDbl1(ByVal T As TextBox) As Double Return Val(T.Text) End Function Sub vivodDblFxy8(ByVal x As Double, ByVal y As Double, _ ByVal T As TextBox) T.Text = T.Text + Format(x, "0.000 ") + Space(8) + _ Format(y, "0.000 ") + vbCrLf End Sub Sub TabFun(ByVal a As Double, ByVal b As Double, _ ByVal h As Double) Dim x, y As Double Dim i, n As Integer x = a n = CInt(((b - a) / h) + 1) For i = 1 To n y = Sqrt(x + 5) + Cos(x ^ 3) vivodDblFxy8(x, y, TextBox4) x = x + h Next i End Sub Private Sub Button1_Click(ByVal sender As System.Object,_ ByVal e As System.EventArgs) Handles Button1.Click Dim aa, bb, hh As Double aa = vvodDbl1(TextBox1): bb = vvodDbl1(TextBox2) hh = vvodDbl1(TextBox3): TabFun(aa, bb, hh) End Sub Private Sub Button2_Click(ByVal sender As System.Object,_ ByVal e As System.EventArgs) Handles Button2.Click End End Sub End Class |
Рис. 4.5.2-20. Программный код процедуры проекта Примера 5.2-8
Тестовые задания
1. Оператор For – это: 1) оператор выбора;2) оператор регулярного цикла3) оператор итеративного цикла4) составной оператор 2. Переменная, изменяющая свое значение при каждом новом вхождении в цикл, называется 1) параметром цикла2) шагом цикла3) индексом4) размером 3. Многократно повторяющаяся часть алгоритма называется 1) телом цикла2) выбором3) перебором4) шагом цикла 4. Циклическая алгоритмическая структура может быть 1) регулярная, итеративная2) регулярная, разветвляющаяся3) итеративная, разветвляющаяся4) нет верного ответа 5. В регулярной циклической структуре число повторений операторов тела цикла 1) заранее известно или может быть предварительно вычислено2) может быть, известно или неизвестно заранее3) заранее неизвестно4) нет верного ответа 6. Тело цикла в операторе For…Next 1) может ни разу не выполниться2) обязательно выполнится хотя бы 1 раз3) выполняется несколько раз 7. Для досрочного прекращения регулярного цикла используется оператор 1) ExitFor 2) Exit 3) Break 4) Exit For8. Для того чтобы операторы тела цикла выполнились необходимое число раз, параметр цикла 1) должен быть переменной вещественного типа2) должен быть переменной целого типа3) должен быть переменной строкового типа4) должен быть переменной целого или вещественного типа 9. Если в операторе регулярного цикла For…Next слово Step отсутствует, это означает, что после каждого выполнения тела цикла 1) параметр цикла увеличивается на 12) параметр цикла уменьшается на 13) параметр цикла изменяется произвольно4) параметр цикла не изменяется 10. Для нахождения наименьшего значения числовой функции от аргумента, значение которого изменяется на заданном интервале, за начальное наименьшее значение следует принять 1) число, близкое к наибольшему числу из диапазона типа данных рассматриваемой функции2) число, близкое к наименьшему числу из диапазона типа данных рассматриваемой функции3) 04) нет верного ответа 11. Для нахождения наибольшего значения числовой функции от аргумента, значение которого изменяется на заданном интервале, за начальное наибольшее значение следует принять 1) число, близкое к наибольшему числу из диапазона типа данных рассматриваемой функции2) 03) нет верного ответа4) число, близкое к наименьшему числу из диапазона типа данных рассматриваемой функции 12. Для нахождения значения произведения числовой функции от аргумента, значение которого изменяется на заданном интервале, за начальное значение произведения следует принять 1) 12) число, близкое к наибольшему числу из диапазона типа данных рассматриваемой функции3) число, близкое к наименьшему числу из диапазона типа данных рассматриваемой функции4) 05) нет верного ответа 13. Для нахождения значения суммы числовой функции от аргумента, значение которого изменяется на заданном интервале, за начальное значение суммы следует принять 1) число, близкое к наибольшему числу из диапазона типа данных рассматривае мой функции2) число, близкое к наименьшему числу из диапазона типа данных рассматривае- мой функции3) 04) 15) нет верного ответа 14. Значение переменной M после выполнения фрагмента программы
| M = 0 For N = 1 To 3 For K = 1 To 2 M = M + 1 Next Next N |
4.5.4. Лабораторная работа по теме «Программирование алгоритмов регулярных циклических структур и циклических структур цикл в цикле»
Цель данной работы состоит в получении навыков разработки проектов, использующих алгоритмы регулярных циклических структур, структур цикл в цикле и освоении стандартного элемента управления ListBox.
Вопросы, подлежащие изучению
1) Циклические алгоритмические структуры.
2) Операторы для программирования регулярных циклов.
3) Базовые алгоритмы регулярных циклических структур.
4) Базовые алгоритмы циклических структур цикл в цикле.
5) Элемент управления ListBox. Добавление, вставка и удаление элементов списка.
Общее задание на разработку двух проектов
1) Изучите вопросы программирования алгоритмов регулярных циклических структур и циклических структур цикл в цикле
(Тема 5).
2) Создайте приложение, состоящее из двух проектов. Первый проект для построения таблицы значений функции y=f(x) одного аргумента, а второй проект для построения таблицы значений функции z=f(x,y) двух аргументов
3) Выберите вариант задания из табл. 4.4.5-1 для создания 1-го проекта и из табл. 4.4.5-2 для создания 2-го проекта.
4) Проведите формализацию поставленной задачи.
5) Составьте схему алгоритма решения поставленных задач.
6) Разработайте интерфейсы пользователя
7) Напишите программный код процедур пользователя для двух проектов в соответствии со схемами алгоритмов. Использовать в качестве параметра цикла переменную целого типа. Обмен данными между процедурами должен осуществляться через параметры, без использования глобальных переменных.
8) Напишите программный код двух проектов. Событийная процедура должна содержать только операторы вызова пользовательских (общих) процедур.
9) Подготовте тесты для контрольного решения задачи.
10) Выполните созданные проекты.
11) Получите результаты выполнения проектов.
12) Обоснуйте правильность полученных результатов на заранее
разработанных тестах для всех ветвей программы.
Варианты индивидуальных заданий
Таблица 4.4.5-1
| № | Задача |
| 1) | Постройте таблицу значений функции y=f(x) при изменении x на отрезке [a;b] c шагом h.
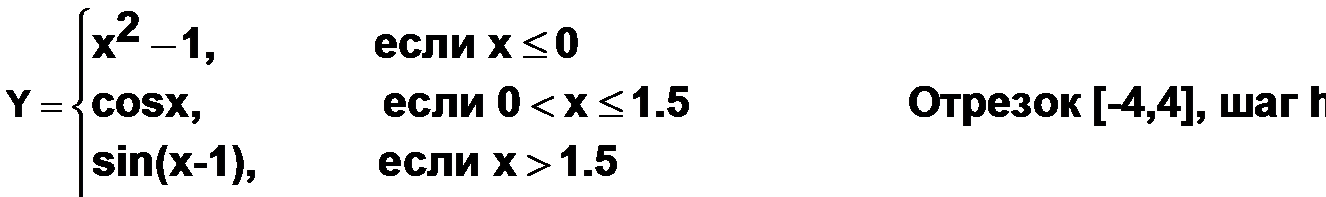
|
| 2) | Постройте таблицу значений функции y=f(x) и найдите наибольшее значение функции y=f(x) при изменении x на отрезке [a;b]c шагом h.
Y=3cos  (2x+1).Отрезок [- (2x+1).Отрезок [-  ], шаг h= ], шаг h=  . .
|
| 3) | Постройте таблицу и найдите наибольшее значение функции y=f(x) при изменении x на отрезке [a;b]c шагом h.
Y=2  .Отрезок[-1,1],шаг h=0.1 .Отрезок[-1,1],шаг h=0.1
|
| 4) | Постройте таблицу и вычислите сумму значений функции y=f(x) при y>0 при изменении x на отрезке [a;b] с шагом h.
 Отрезок [- Отрезок [-  ], шаг h= ], шаг h= 
|
| 5) | Постройте таблицу значений функции y=f(x) при изменении x на отрезке[a;b]c шагом h
 Отрезок [-3;3], шагh=0.25 Отрезок [-3;3], шагh=0.25
|
| 6) | Постройте таблицу и найдите наибольшее значение функции y=f(x) при изменении x на отрезке[a; b]c шагом h.
Y=0.5  . Отрезок [0,10], шаг h=0.5 . Отрезок [0,10], шаг h=0.5
|
| 7) | Постройте таблицу и вычислите произведение значений функции y=f(x) при y>0 при изменении x на отрезке [a; b] с шагом h.
Y=x  Отрезок [0;10],шаг h=0.5 Отрезок [0;10],шаг h=0.5
|
| 8) | Постройте таблицу значений функции y=f(x) при изменении x на отрезке[a; b]c шагом h.
Y=  Отрезок[-2;2],шаг h=0.25 Отрезок[-2;2],шаг h=0.25
|
| 9) | Постройте таблицу и найти наибольшее значение функции y=f(x) при изменении x на отрезке [a;b]c шагом h.
Y=  Отрезок[0.1;1.5],шаг h=0.1 Отрезок[0.1;1.5],шаг h=0.1
|
| 10) | Построите таблицу и вычислить сумму значений функции y=f(x) при y<0 и при изменении x на отрезке [a,b] с шагом h.
Y=0.5-0.1-sinx Отрезок [0,2  ], шаг h= ], шаг h= 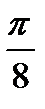
|
| 11) | Постройте таблицу значений функции y=f(x) при изменении x на отрезке[a; b]c шагом h.
Y=  Отрезок[-2;2],шаг h=0.25 Отрезок[-2;2],шаг h=0.25
|
| 12) | Постройте таблицу и вычислите произведение значений функции y=f(x) при y<0 при изменении x на отрезке [a; b] с шагом h.
Y=  .Отрезок[-1.5,1.5], шаг h=0.15 .Отрезок[-1.5,1.5], шаг h=0.15
|
| 13) | Постройте таблицу и найдите наибольшее значение функции y=f(x) при изменении x на отрезке [a; b]c шагом h.
 . Отрезок[-5,5],шаг h=0.5 . Отрезок[-5,5],шаг h=0.5
|
| 14) | Постройте таблицу и вычислите сумму значений функции y=f(x) при 0.5<y<1.5 при изменении x на отрезке [a; b] с шагом h.
Y=1+cos10x.Отрезок[  ],шаг h= ],шаг h=  . .
|
| 15) | Постройте таблицу и найдите наименьшее значение функции y=f(x) при изменении x на отрезке [a; b]c шагом h. Y=x+1/x. Отрезок [0.1;1.5], шаг h=0.1 |
| 16) | Постройте таблицу и вычислите произведение значений функции y=f(x) при y>0 при изменении x на отрезке [a; b] с шагом h.
Y=  . Отрезок[-0.5;1.5],шаг h=0.1 . Отрезок[-0.5;1.5],шаг h=0.1
|
| 17) | Постройте таблицу значений функции y=f(x) при изменении x на отрезке [a; b]c шагом h.
Y= 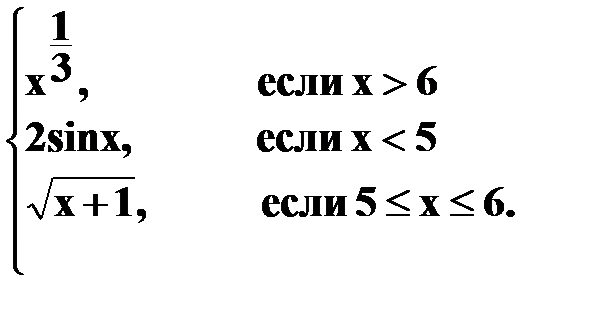 Отрезок[2;12],шаг h=0.5 Отрезок[2;12],шаг h=0.5
|
| 18) | Постройте таблицу значений функции y=f(x) при изменении x на отрезке [a; b]c шагом h.
Y=  Отрезок[-2;6],шаг h=0.5 Отрезок[-2;6],шаг h=0.5
|
| 19) |
Постройте таблицу и найдите наибольшее значение функции y=f(x) при изменении x на отрезке [a;b]c шагом h.
Y=  . Отрезок[2;4],шаг h=0.1 . Отрезок[2;4],шаг h=0.1
|
| 20) | Постройте таблицу значений функции y=f(x) при изменении x на отрезке [a;b]c шагом h.
Y= 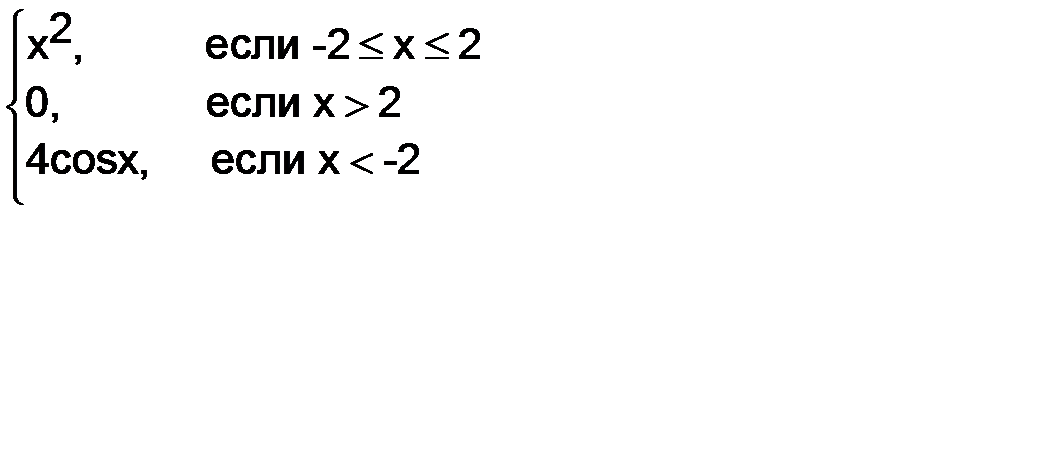 Отрезок[-3;3],шаг h=0.3 Отрезок[-3;3],шаг h=0.3
|
| 21) | Постройте таблицу и найдите наибольшее значение функции y=f(x) при изменении x на отрезке [a; b]c шагом h.
 . Отрезок[6;8]шаг h=0.2 . Отрезок[6;8]шаг h=0.2
|
| 22) | Постройте таблицу и вычислите сумму значений функции y=f(x) при y<1.2при изменении x на отрезке [a; b]c шагом h.
Y=sin(4x)-2. Отрезок [-  ], шаг h= ], шаг h= 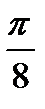
|
| 23) | Постройте таблицу значений функции y=f(x) при изменении x на отрезке [a; b]c шагом h.
Y=  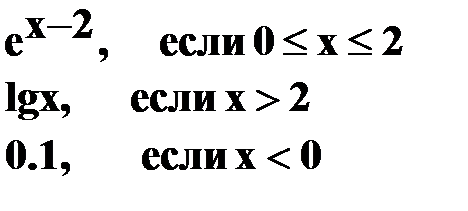 Отрезок[-4;4], шаг h=0.5 Отрезок[-4;4], шаг h=0.5
|
| 24) | Постройте таблицу и вычислите произведение значений функции y=f(x) при y>0 при изменении x на отрезке [a; b]c шагом h.
Y=  .Отрезок[-3;0],шаг h=0.15 .Отрезок[-3;0],шаг h=0.15
|
| 25) | Постройте таблицу и найдите наибольшее значение функции y=f(x) при изменении x на отрезке [a; b]c шагом h.
Y=arctg(x)-  . Отрезок [0.1;1.5],шаг h=0.1 . Отрезок [0.1;1.5],шаг h=0.1
|
| 26) | Постройте таблицу и вычислите сумму значений функции y=f(x) при y>0 при изменении x на отрезке [a; b]c шагом h.
 . Отрезок [0; . Отрезок [0;  ],шаг h= ],шаг h= 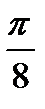
|
| 27) | Постройте таблицу и найдите наибольшее значение функции y=f(x) при изменении x на отрезке [a; b] c шагом h.
 .Отрезок[0.1;1.5],шаг h=0.1 .Отрезок[0.1;1.5],шаг h=0.1
|
| 28) | Постройте таблицу и вычислите произведение значений функции y=f(x) при y>0 при изменении x на отрезке [a; b] с шагом h.
Y=  . Отрезок[1.9;2.1],шаг h=0.01 . Отрезок[1.9;2.1],шаг h=0.01
|
| 29) |
Постройте таблицу и вычислите наименьшее значение функции y=f(x) при изменениях х на отрезке [a; b] с шагом h.
Y=5*sin( x+1)^2. Отрезок[- x+1)^2. Отрезок[-  ], шаг h= ], шаг h= 
|
| 30) | Постройте таблицу и вычислите наибольшее значение функции y=f(x) при изменениях х на [a; b]c шагом h.
Y=5*sin( x+1)^4- cos(x). Отрезок[- x+1)^4- cos(x). Отрезок[-  ], шаг h= ], шаг h= 
|
Таблица 4.4.5.2
| № | Задача |
| 1) | табл. 5-1 для создания 1-го проекта и найдите наибольшее значение функции при изменении xна отрезке [a;b] с шагом h1 и y на отрезке [c; d] с шагом h2. a= - π b= π c= - π d= π h1=π/8 h2=π/4 z(x,y)= 3 cos2(2*x+y+1) |
| 2) | Постройте таблицу значений функции z=f(x,y)и найдите сумму и количество положительных значений функции при изменении x на отрезке [a;b] с шагом h1и y на отрезке [c; d] с шагом h2. a= - π b= π c= - π d= π h1=π/6 h2=π/4 z(x,y)= 1/(x+2*π-y) – sin(x) |
| 3) | Постройте таблицу значений функции z(x,y)при изменении x на отрезке [a;b] с шагом h1и y на отрезке [c; d] с шагомh2. а= - 1 b= 2 h1= 0.1 c = - 1 d=2 h2=0.2 x^2 + y^2если 0≤ x ≤ 1 и 0 ≤ y ≤ 1, z(x,y)= x - y если -1≤ x ≤0 и -1≤ y ≤0, 1 – x - y в противном случае |
| 4) | Постройте таблицу значений функции z=f(x,y) и найдите произведение и количество положительных значений функции при изменении x на отрезке [a;b] с шагом h1 и y на отрезке [c; d] с шагом h2. a= 0 b= 10 c= - 2 d= 2 h1= 0.5 h2=0.2 z(x,y)=x^4 +y- 10*x^2 – 30*x -25 |
| 5) | Постройте таблицу значений функции z=f(x,y)и найдите наименьшее значение функции при изменении xна отрезке[a; b]с шагомh1иyна отрезке[c; d]с шагомh2. a= 0.1 b= 1.5 c= 1 d=2 h1=0.1 h2=0.1 z(x,y) = x + 1/x + (1 - y)/2 |
| 6) | Постройте таблицу значений функции z=f(x,y) и найти сумму и количество отрицательных значений функции при измененииxна отрезке[a; b]с шагомh1иyна отрезке[c; d]с шагомh2. a= 0 b= 2π c=0 d=2π h1=π/8 h2=π/8 z(x,y)= y – 0.1*sin(x)/2 |
| 7) | Постройте таблицу значений функции z(x,y)при изменении x на отрезке [a; b] с шагом h1и y на отрезке [c; d]с шагом h2. a= -3 b= 4 c = -2 d=2 h1= 0.25 h2=0.25 e^x + y если x € [-2;2] и y € [-1;1], z(x,y)= x+y+4 если -3 <x<-2 и - 2< y< - 1, 0 в противном случае |
| 8) | Постройте таблицу значений функции z=f(x,y) и найдите произведение и количество отрицательных значений функции при изменении x на отрезке [a; b] с шагом h1 и y на отрезке [c; d] с шагом h2. a= -1.5 b= 1.5 c= -2 d= 2 h1= 0.2 h2= 0.2 z(x,y)= x^8-y- 0.4*x^3 – 1.2 |
| 9) | Постройте таблицу значений функции z=f(x,y)и найдите наименьшее значение функции при изменении xна отрезке [a; b]с шагомh1иyна отрезке[c; d]с шагомh2.
a= 0.1 b=1.5 h1=0.1 c=2 d=3 h2=0.1 z(x,y) = 
|
| 10) | Постройте таблицу значений функции z(x,y) и найдите сумму и количество положительных значений функции при изменении xна отрезке [a; b] с шагом h1 и yна отрезке [c; d] с шагом h2. a= -π b= π h1=π/8 c= - π d= π h2=π/6 z(x,y)= sin(4x+y) – 2*x |
| 11) | Постройте таблицу значений функции z(x,y) при изменении x на отрезке [a; b] с шагом h1 и yна отрезке [c; d] с шагом h2.
a= 1 b=5 h1= 0.2 c=0 d=6 h2=0.4
x +y если x € [2;4] и y € [1;5],
z(x,y)=  если 1< x <2 и 0<y<1,
x - y в противном случае если 1< x <2 и 0<y<1,
x - y в противном случае
|
| 12) | Постройте таблицу значений функции z=f(x,y) и найдите произведение и количество отрицательных значений функции при изменении x на отрезке [a; b]с шагомh1иyна отрезке[c; d]с шагомh2.
a=1.9 b=2.1 h1=0.01 c=2 d=3 h2=0.1
z(x,y)= 
|
| 13) | Постройте таблицу значений функции z=f(x,y) и найдите наименьшее значение функции при изменении xна отрезке[a; b]с шагомh1иyна отрезке[c; d]с шагомh2.
a= 2.1 b=3 h1=0.1 c=2 d=3 h2=0.2 z(x,y) = 
|
| 14) | Постройте таблицу значений функции z=f(x,y) и найдите сумму и количество значений функции  >0.1 при изменении xна отрезке[a; b]с шагомh1иyна отрезке[c; d]с шагомh2.
a=0 b= π h1= π/16 c=0 d=3 h2=0.1z(x,y)= >0.1 при изменении xна отрезке[a; b]с шагомh1иyна отрезке[c; d]с шагомh2.
a=0 b= π h1= π/16 c=0 d=3 h2=0.1z(x,y)= 
|
| 15) | Постройте таблицу значений функции z(x,y)при измененииxна отрезке[a; b]с шагомh1иyна отрезке[c; d]с шагомh2.
a= -2 b= 5 h1=0.5 b= 0 c=3 h2= 0.1
 если x€[-1;4] и y€ [1;2]
z(x,y)= x – 3 + y если -2 < x < -1 и 0< y <1 если x€[-1;4] и y€ [1;2]
z(x,y)= x – 3 + y если -2 < x < -1 и 0< y <1
 в противном случае в противном случае
|
| 16) | Постройте таблицу значений функции z=f(x,y) и найдите произведение и количество значений функции z(x,y) < 1 при изменении x на отрезке [a; b]с шагомh1иyна отрезке [c; d]с шагомh2.
a= -π b= π h1=π/8 c= -π d= π h2=π/8
z(x,y)= 
|
Постройте таблицу значений функции z=f(x,y)и найдите наибольшее значение функции при изменении xна отрезке[a; b]с шагомh1иyна отрезке[с; d]с шагом h2.
a=-1.9 b= 2.9 h1=0.03 c= 1 d=2 h2=0.1 z(x,y)= Y+  . .
| |
| 18) | Постройте таблицу значений функции z=f(x,y)и вычислите наименьшее значение функции при изменении xна отрезке[a; b]с шагомh1иyна отрезке [c; d] с шагом h2.
a= -3 b=3 h1=0.2 c= 1 d=2 h2= 0.1
z(x,y)=  + y + y
|
| 19) | Постройте таблицу значений функции z=f(x,y) и найдите сумму и количество значений функции при z>0при измененииxна отрезке [a; b]с шагомh1и yна отрезке[c; d]с шагомh2.
a= -1.9 b= 2.9 h1=0.3 c=2 d=3 h2=0.1 z(x,y) =  - y - y
|
| 20) | Постройте таблицу значений функции z=f(x,y)при измененииxна отрезке [a; b]c шагомh1иyна отрезке[c; d]с шагомh2.
a= -4 b=4 h1=0.5 c=2 d=3 h2=0.1
z(x,y)= 
|
| 21) | Постройте таблицу значений функции z=f(x,y)и найдите сумму и количество значений функции приz<1.5при измененииxна отрезке[a; b]c шагомh1иyна отрезке[c; d] с шагомh2. a= -π b=π h1=π/8 c= -π d=π h2=π/8 z(x,y)=sin(4x+y) - 2 |
| 22) | Постройте таблицу значений функции z=f(x,y) и найдите наибольшее значение функции при изменении x на отрезке [a; b]c шагомh1иy на отрезке [c; d]с шагомh2.
a= 6 b=8 h1= 0.2 c=2 d=3 h2=0.1
z(x,y)= 
|
| 23) | Постройте таблицу значений функции z=f(x,y)и найдите произведение и количество значений функции при z<3 при измененииxна отрезке[a; b]с шагомhиyна отрезке [c; d]с шагом h2.
a= 1.9 b=2.1 h1=0.01 c=2 d=3 h2=0.02 z(x,y)=  . + y . + y
|
| 24) | Постройте таблицу значений функции z=f(x,y)при измененииxна отрезке[a; b]c шагомh1иyна отрезке[c; d]с шагомh2. a=0 b=3 h1=0.1 c=1 d=4 h2=0.2 x+y-1 если x€ [1;2] и y€ [2;3] z(x,y)= x-y если 0<x<1 и 3<y<4 12.3 в противном случае |
| 25) | Постройте таблицу значенийфункции z=f(x,y)и найдите наименьшее значение функции при изменении x на отрезке [a; b]с шагомh1и yна отрезке [c; d]с шагом h2. a= -π b=π h1=π/8 c=2 d=3 h2=0.1 z(x,y)= 5*sin(2*x+1)^2 + y |
| 26) | Постройте таблицу значений функции z=f(x,y) и найдите сумму и количество значений функции z(x,y)>0 при изменении xна отрезке[a; b]с шагомh1и yна отрезке [c; d]с шагомh2. a= -2 b=5 h1= 0.2 c=0.1 d=0.2 h2=0.01 z(x, y)= x + y - x/y |
| 27) | Постройте таблицу значений функции z=f(x,y)и найдите произведение и количество значений функции z(x,y) < 0при измененииxна отрезке [a; b]с шагомh1и yна отрезке [c; d]с шагомh2. a= 20 d=30 h1= 5 c= 10 d=50 h2=5 z(x,y)=17.5 + x – y |
| 28) | Постройте таблицу значений функции z=f(x,y)и найдите наибольшее значение функции при измененииxна отрезке[a; b]с шагомh1иyна отрезке[c; d]с шагомh2.
a= - 5 b=5 h1= 0.5 c= 0.1 d=0.3 h2=0.02 z(x,y) = 
|
| 29) | Постройте таблицу функции z=f(x,y)и найдите сумму и количество значений функции при z>0при изменении xна отрезке[a; b]с шагомh1иyна отрезке[c; d]с шагом h2.
a= -2 b=2 h1=0.5 c=2 d=3 h2=0.1 z(x,y)= x/y + (x+y)/2 - 
|
| 30) | Постройте таблицу значений функции z=f(x,y)при измененииxна отрезке[a; b]c шагомh1иyна отрезке[c; d]с шагомh2. a= 0.1 b=0.8 c= 0.2 d= 0.6 h2=0.05 Sin(x+y) если x€[0.5; 0.7] и y € [0.3;0.4] z(x,y)= x-y если 0.1<x<0.5 и y € [0.4;0.6] 1 в противном случае |
4.5.4.4. Содержание отчёта
1) Фамилия, имя студента, номер группы, номер варианта.
2) Реализация 1-го задания:
2.1) Тема и название лабораторной работы.
2.2) Задание на разработку задачи.
2.3) Формализация и уточнение задания.
2.4) Элементы, разрабатываемого проекта:
2.4.1) графический интерфейс пользователя;
2.4.2) таблица свойств объектов;
2.4.3) схемы алгоритмов;
2.4.4) программный код проекта;
2.5) Результаты выполнения первого проекта.
2.6) Доказательства правильности результатов.
3) Реализация 2-го задания:
3.1) Тема и название лабораторной работы.
3.2) Задание на разработку задачи.
3.3) Формализация и уточнение задания.
3.4) Элементы, разрабатываемого проекта:
3.4.1) графический интерфейс пользователя;
3.4.2) таблица свойств объектов;
3.4.3) схема алгоритма;
3.4.4) программный код проекта;
3.5) Результаты выполнения проекта второго проекта.
3.6) Доказательства правильности результатов.






