Общая задача прогнозирования значений случайных величин. Прогнозирование осуществляется на базе знаний и данных, которыми мы обладаем

Прогнозирование осуществляется на базе знаний и данных, которыми мы обладаем. Смысл: мы хотим вместо случайной величины получить число.

- оценивание

- понятие простых случайных величин.

 

билет N18

1. Построение оптимальных критических областей.

Пример про покрышки: гипотеза о среднем износе.

-принимаем гипотезу, при «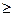» - отвергаем.

- граничная точка.

Иногда можно применить простые интуитивные решения.

Понятие критической области

Критической областью гипотезы Н называется такая область в выборочном пространстве в которую с вероятностью α попадет результат эксперимента если -верна.

 

билет N19

Количественные характеристики риска.

Для всех свой риск. Риск должен измеряется в понятных нам величинах. Напр. для бегуна – секунда, для силача – кг и т.д. Только для сравнительных единиц. Нет понятия большой и малой вероятности.

 

. 2. Выбор решений по среднему значению критерия.

Решение всегда принимается по среднему значению критерия, потому что это оптимальный вариант. К примеру, за критерий берём отклонение от среднего.

билет N20

1. Стоимости рисков и примеры их использования.

Под стоимостью риска следует понимать фактические убытки предпринимателя, затраты на снижение величины этих убытков или затраты по возмещению таких убытков и их последствий.

или ввести цену ошибки ф(q-x) и min M[ф(q-x)].

где М – оператор матожидания.

отсюда мы найдем оптимальное q.

2. Параметрические гипотезы.

Предположение,о том что неизвестный параметр принадлежит некоторому множеству значений. Параметрической гипотезой H(w,W) называется утверждение

qÎw,

где q — неизвестный параметр,

W — множество всех возможных значений q,

w — подмножество W.

 

 

билет N21

1. Понятие ошибок первого и второго рода.

Ошибка первого рода – гипотеза H₀ справедлива, но она отвергнута. Ошибка второго рода – гипотеза H₀ ложна, но она принята.

2. Линейное оценивание значений случайных величин.

Оценка является линейной если она является линейной комбинацией результатов наблюдения

 

 

билет N22

1. Риски при формировании портфеля ценных бумаг.

Распределительная задача. Формирование разбиения: сколько куда денег вложить (в какие ценные бумаги).

Цели анализа риска.

Обработка данных ведется для принятия решений. Если решение не принято: в мире ничего не изменится – главная цель: принять решение.

 

 

N23

1. Риски при инвестировании средств.

Риски могут быть системными и несистемными. Первые характерны для всех инвестиций, а вторые эпизодические и временные. Несистемные риски можно снизить только за счет диверсификации.

Есть и специфические виды риска, которые присущи в основном для облигаций и акций.

Риск дефолта или кредитный риск. Данный риск связан с неспособностью предприятия или отдельного лица выполнить собственные долговые обязательства. Риск характерен для корпоративных и муниципальных облигаций. Облигациям, которые имеют низкий уровень риска, присваивается определенный инвестиционный рейтинг, а высокорисковые облигации называются «мусорными». Благодаря рейтингу облигаций, инвестор может избежать ненужного риска.

Региональным рискам подвержены ценные бумаги конкретных стран, регионов. Данный риск характерен для развивающихся стран, имеющих большой уровень внешнего и внутреннего долга.

Есть риски, связанные с разницей в курсах валют, с изменением процентного дохода, с изменением политики правительства конкретной страны, с уровнем волатильности (опционы и акции). Многие из этих рисков инвестору приходится принимать во внимание при выборе вариантов для инвестирования средств.

2. Отображение выборочного пространства на множество гипотез.

 

Пусть имеются две гипотезы:

H(w,W)

H(W\w,W) //над этой Н надо еще черточку нарисовать, это альтернативная гипотеза

w — то подмножество W, значения в котром согласно основной гипотезе H должен принять параметр

W — множество всех возможных значений параметра.

 

билет N24

1. Прогнозирование значений случайных величин при среднеквадратическом критерии оптимальности.

Самая хорошая оценка прогноза значений случайных величин при среднеквадратическом критерии оптимальности – математическое ожидание.

2. Отображение выборочного пространства на множество гипотез.

Пусть имеются две гипотезы:

H(w,W)

H(W\w,W) //над этой Н надо еще черточку нарисовать, это альтернативная гипотеза

w — то подмножество W, значения в котром согласно основной гипотезе H должен принять параметр

W — множество всех возможных значений параметра.