Как практически определяются напряжения в инженерной практике от действия сосредоточенной нагрузки.

Согласно рис.в вопросе 51 точка М вполне определяется двумя её координатами Z и r. После некоторых преобразований будем иметь:

Для облегчения расчетов служит таблица (Ц. стр79). Величина К определяется для ряда значений r/ z.

 

53. Как следует просуммировать напряжения, если действует несколько сосредото-ченных сил?

Если на поверхности массива приложено несколько сосредоточенных сил Р₁, Р₂, Р₃ …,

то сжимающие напряжения в любой точке массива для горизонтальных площадок, параллельных ограничивающей плоскости, может быть найдено простым суммированием, так как вывод формулы в вопросе 52 основан на прямой пропорциональности между напряжениями и деформациями:

.

 

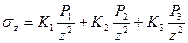54. Какое условие накладывается на эпюры напряжений для выполнения условия равновесия?

Для выполнения условия равновесия необходимо, чтобы в случае пространственной задачи объем эпюры σ _z при заданной постоянной величине z равнялся бы действующей сосредоточенной силе.

В случае плоской задачи это условие сохраняется, однако оно упрощается, и поэтому площадь эпюры σ _z при постоянной величине z должна быть равна внешней нагрузке.

 

55. В чем заключается принцип Сен-Венена в теории упругости?

Принцип Сен-Венена заключается в том, что с удалением от места приложения усилия напряжения оказываются все менее зависящими от характера этого усилия (сосредоточенная сила, несколько сосредоточенных сил или распределенная на конечном участке нагрузка) при условии, если равнодействующая всех усилий, приложенных на границе, одинакова.

 

56. Распределение напряжений в случае плоской задачи. Когда имеет место случай плоской задачи?

Условия плоской задачи будут иметь место в случае, когда напряжения распределяются в одной плоскости, в направлении же перпендикулярном они будут или равны нулю, или постоянны. Это условие имеет место для очень вытянутых в плане сооружений, например ленточных и стеновых фундаментов, оснований подпорных стенок, насыпей, дамб и подобных сооружений.

 

57. Действие равномерно распределённой нагрузки. Зависят ли составляющие напряжений σ_z, σ_y, и τ в плоскости от деформационных характеристик? Какой угол называется «углом видимости» и почему?

Определение напряжений в условиях плоской задачи значительно упрощается и следует отметить весьма важное свойство плоской задачи, заключающееся в том, что все составляющие напряжений σ_z, σ_y, и τ в плоскости от деформационных характеристик не зависят и будут справедливы для всех тел (сплошных, сыпучих и т. п.), для которых зависимость между напряжениями и деформациями может быть принята линейной.

 

Из рисунка удобно ввести две безразмерные координаты - два угла α и β. Угол α называется углом видимости, поскольку если мы поместим в рассматриваемую точку полуплоскости глаз наблюдателя, то под этим углом мы как бы видим нагрузку. Второй угол β между вертикалью, проходящей через данную точку, и биссектрисой угла видимости α.

58. Какие напряжения называются главными нормальными и какие главными касательными? Сколько главных напряжений в плоской и сколько в пространственной задачах?

Главные нормальные напряжения - это нормальные напряжения, действующие на площадки, на которых отсутствуют касательные напряжения. Главные касательные напряжения - это максимальные касательные напряжения. Если обозначить главные нормальные напряжения через σ₁, σ₂, σ₃,то главные касательные напряжения равны соответственно:

; ; ;

Главных нормальных напряжений в пространственной задаче - три, в плоской - два. Главных касательных напряжений в случае пространственной задачи - три, в случае плоской задачи - одно.

 

59. Какой вид имеют эпюры вертикальных нормальных напряжений σ_z, в случае плоской задачи, когда на участке границы приложена равномерно распределенная нагрузка?

Эпюры вертикальных нормальных напряжений σ_z изображены на рисунке:

 

60. Что такое изолинии напряжений и какой вид имеют изолинии главных напряжений в случае плоской задачи, когда на участке границы полуплоскости приложена равномерно распре­деленная нагрузка?

Изолинии напряжений - это линии, во всех точках которых соответствующие напряжения равны. Изолинии главных напряжений, как наибольшего, так и наименьшего, представляются дугами окружностей, проходящих через концевые точки загруженного участка.

61. Чему равны σ_z, σ_y и τ в случае действия равномерно распределённой нагрузки?

Из обозначений рисунка в вопросе 57 справедливы следующие выражения:

;

;

;

 

Приведенные выражения позволяют составить таблицу коэффициентов влияния К_z, К_y и К_yz (Н.А.Цытович, Механика грунтов, стр. 93) и введя следующие обозначения

 

;

;

,

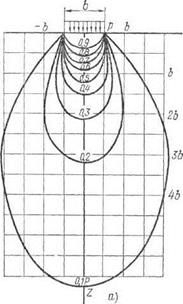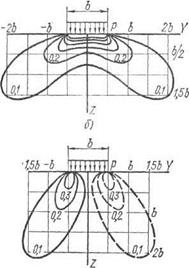построить эпюры распределения напряжений по горизонтальным и вертикальным сечениям массива грунта в случае плоской задачи (при полосовой равномерно распределённой нагрузке).

в)

а) изобыры σ_z б) распоры σ_y

в) сдвиги τ_zy

 

62. Какие напряжения считают главными?

Главные – это наибольшие и наименьшие нормальные напряжения для площадок, расположенных по вертикальной оси симметрии нагрузки.

Величину главных напряжений получим из выражений (вопрос 61) полагая в них β =0 ;

 

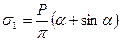Эллипсы напряжений при действии равномерно распределённой

нагрузки в условиях плоской задачи

 

63. Какая задача называется контактной?

Вопрос о распределении давлений по подошве сооружений имеет большое практическое значение, особенно для гибких фундаментов, рассчитываемых на изгиб. Контактная задача- это решение вопросов о распределении давлений по подошве сооружений, опирающихся на грунт. Если известно реактивное давление по подошве фундамента, которое обычно и называют контактным, то, приложив к подошве фундамента его обратную величину находят величину расчетных изгибающих моментов и перерезывающих сил, применяя известные уравнения статики,

64. Какое исходное уравнение для решения контактной задачи? Какую роль играет жесткость фундамента?

 

Исходным уравнением для решения контактной задачи является формула Буссинеска для перемещений (см. вопрос 51). Выведены формулы перемещений для круглого жесткого и гибкого фундаментов и получены эпюры контактных давлений:

Рис.64.1.Эпюры контактных давлений

а) под абсолютно жестким фундаментом; б) под фундаментом различной гибкости

 

64.2. Изобары в грунте под фундаментами:

а) жестким; б) гибким.

По решениям, излагаемым в курсе сопротивление материалов, эпюра контактных давлений будут прямолинейна – равномерна или трапецеидальна, тогда как по строгому решению теории упругости для жестких фундаментов она всегда будет седлообразной, а для фундаментов конечной жесткости (гибких) эпюра может принимать очертание от седлообразного до параболического.

 

65. Что понимается под предельным напряженным состоянием грунта?

Предельное напряженное состояние грунта в данной точке соответствует такому напряженному состоянию, когда малейшее добавочное силовое воздействие нарушает существующее равновесие и приводит грунт в неустойчивоё состояние: в массиве грунта возникают поверхности скольжения, разрывы и нарушается прочность между его частицами и агрегатами. Такое напряженное состояние грунтов следует рассматривать как совершенно недопустимое при возведении на них сооружений.

 

66. Каков график деформаций грунта при действии на его поверхности возрастаю-щей ступенями нагрузки?

На рисунке а) приведена типичная кривая деформаций грунта при действии возрастающей нагрузки. Если нагрузка мала и грунт обладает связностью, то первые участки на кривой будут почти горизонтальны (начальный участок показан на рис.). На следующих ступенях нагружения происходит уплотнение грунта, уменьшение пористости. Конец фазы уплотнения (точка С) и начало зон сдвигов. Далее фаза сдвигов переходит в пластическое течение и недопустимые деформации основания (точка d).

Зависимость между деформациями и напряжениями в этой фазе нелинейная.

На рисунке в) показан конец фазы уплотнения - начало фазы сдвигов

На рисунке г) – линии скольжения и уплотненное ядро при полном развитии зон предельного равновесия.

67. Условия предельного равновесия для сыпучих и связных грунтов?

а) б)

 

в)

 

На рисунке показаны круги предельных равновесий: а) схема напряжений в данной точке М;

б) диаграмма сдвига для сыпучих грунтов; в) то же, для связных грунтов.

б) - для сыпучих грунтов согласно диаграмме сдвига максимальное значение угла отклонения θ _max,будет тогда, когда огибающая ОЕ коснется круга предельных

напряжений, и тогда:, ; после тригонометрических преобразований:

, или .

это и есть условие предельного равновесия для сыпучих (не связных) грунтов.

в)-для связных грунтов, подобно предыдущему, пользуясь диаграммой предельных напряжений, получим:

, откуда , (67.1)

а т.к. , где с - сцепление грунта, определяемое как начальный параметр

огибающей кругов предельных напряжений окончательно получим условие предельного равновесия в в состовляющих напряжениях σ_z σ_y. τ для связных грунтов.

 

68. Что понимается под критическими нагрузками на грунт и как они определяются? Формула Н.П. Пузыревского.

Установлены (при давлениях на грунт, больших структурной прочности) две критические нагрузки: 1-нагрузка, соответствующая началу возникновения в грунте зон сдвигов и окончанию фазы уплотнения, когда под краем нагрузки возникает предельное напряжённое состояние. И 2- нагрузка, при которой под нагруженной поверхностью сформировываются сплошные области предельного равновесия, грунт приходит в неустойчивое состояние и полностью исчерпывается его несущая способность.

;

если принять z =0, т.е. ни в одной точке грунта не будет зон предельного равновесия,

начальным критическим давлением на грунт будет:

нач .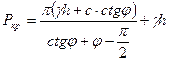

Это и есть формула проф. Н.П. Пузыревского для начальной критической нагрузки на грунт. Определяемое по ней давление можно рассматривать как совершенно безопасное.

Вторая критическая нагрузка, это предельная нагрузка, соответствующая полному исчерпанию несущей способности грунта и сплошному развитию зон предельного равновесия, что достигается для оснований фундаментов при окончании формирования жесткого ядра, деформирующего основание и распирающего грунт в стороны.

Впервые эта задача для невесомого грунта, нагруженного полосовой нагрузкой была решена Прандтлем и Рейснером (1920-1921):

пред .

 

 

69. Каким образом происходит процесс развития областей пластических деформаций под фундаментом с ростом нагрузки?

 

Рост областей с предельным состоянием в основании с увеличением нагрузки р

Считатется, что области пла­стических деформаций зарожда-ются у краев фундамента; далее с ростом нагрузки они распро-страняются вглубь и начинают заходить под фундамент (см.рис.). Наконец, при на­грузке, достигающей несущей способности основания, обе об­ласти пластических деформаций смыкаются на оси фундамента и происходит резкое проседание его вниз.

 

 

70. Какой вид имеет схема расчета несущей способности основания "по Прандтлю"? Что называется "упругим ядром" и где оно находится?

При расчете величины несущей способности "по Прандтлю" предполагается существование трех зон: зоны с максимально напряженным состоянием I (или зоны пассивного давления), зоны с минимально напряженным состоянием II (или зоны активного дав-ления) и переходной.между ними зоны III, позволяющей получить плавное изменение напряжений без скачков в них. При этом предполагается, что нагрузка является равномерной и не имеет горизонтальной составляющей. В действительности мы приклады­ваем нагрузку с помощью жесткого шероховатого штампа, поэтому непосредственно под ним вместо зоны с минимально напряженным предельным состоянием формируется зона, в которой нет предель­ного состояния и которая как бы сливается со штампом, составляя с ним одно целое. Эта зона называется "упругим" или "жестким" ядром. (см.рис.).

 

 

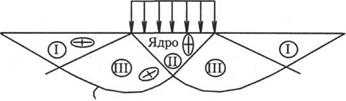
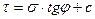
Очертание различных по характеру напря­женного состояния предельных зон по схеме Прандтля

 

 

70. Что понимают под осадкой фундаментов и из каких величин она складывается?

Осадками фундаментов сооружений называются их вертикальные смещения, вызванные деформацией их основания под действием нагрузки от сооружения.

При возведении фундаментов общая осадка их в условиях современного строитель-ства складывается из трёх величин: 1-неупругой (структурной) полностью остаточной осадки деформаций верхнего слоя грунта при подготовке котлованов землеройными машинами; 2- пластических местных выдавливаний грунта (вследствие неровностей поверхности) в момент установки фундаментов и их загрузки и 3- длительных осадок уплотнения и затухающей ползучести сжатой зоны грунта под фундаментами.

70. Что необходимо знать, чтобы приступить к расчету осадки фундамента?

Прежде чем приступить к расчету необходимо знать:

1) геологическое строение места строительства с указанием мощности (толщины) отдельных слоёв грунта, уровня грунтовых вод и физико-механических свойств грунтов основания на всю активную зону сжатия (коэффициенты пористости, сжимаемости, плотноти всех элементов грунта, характеристики прочности (угол внутреннего трения, сцепление), а также для связных грунтов- коэффициент фильтрации, структурной прочности, начального градиента напора и для плотных и вязких глин-параметров ползучести);

2) размеры и форму фундамента (по предварительным расчетам) и чувствитель-ность сооружений (разрезных, жестких рамных, массивных и т.п.) к неравномерным осадкам;

3) данные о глубине заложения фундамента и нагрузке на грунт от надфундамент-ных конструкций.

 

71. Чему равна осадка слоя грунта при сплошной нагрузке (основная задача)?

При действии сплошной нагрузки (распространённой на значительные расстояния в стороны) слой грунта (см. рис.) будет испытывать только сжатие без возможности бокового расширения (аналогично компрессионным испытаниям). Т.е. имеем одномерную задачу компрессионного уплотнения грунтов, и для определения полной стабилизацион-ной осадки пользуются компрессионной кривой (см. рис.)

Осадка S равна разности высот грунта до уплотнения нагрузкой и после:

; или , это и есть формула для полной осадки, а

учитывая, что (см. закон уплотнения) ,

здесь 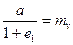= есть коэффициент относительной сжимаемости, и подставив m _v

получим S=hm_vP или

Формула справедлива для любых грунтов в пределах линейной зависимости между σ и ε.

 

72. Изменяется ли осадка фундаментов зданий с течением времени? От чего зависит осадка?

Осадки не заканчиваются за время строительства (исключение составляют лишь чистые пески). На процесс развития осадок во времени влияет как водопроницаемость грунтов, так и ползучесть скелета грунта, а также деформируемость всех компонентов, составляющих грунт (поровой воды, включений воздуха, паров и газов, органических веществ и т.п.).

Водонасыщенные пластичные и особенно текучепластичные (слабые) глинистые грунты дают наибольшие осадки, часто весьма медленно затухающие, и создают наибольшие затруднения для строителей. Осадки сооружений на этих грунтах могут достигать сотен сантиметров и протекать десятки и сотни лет.

 

73. Какая теория используется при определении осадки во времени и её предпосылки?.

Для полностью водонасыщенных грунтов наиболее широко применяемой в настоящее время теорией, позволяющей решать поставленные задачи, является теория фильтрационной консолидации грунтов.

Предпосылки теории фильтрационной консолидации:

1) рассматривается полностью водонасыщенные грунты;

2) скелет грунта принимается линейно деформируемым, напряжения в котором мгновенно вызывают его деформации;

3) грунт не обладает структурностью, и внешнее давление, прикладываемое к нему, в первый момент времени полностью передаётся на воду;

4) фильтрация воды в порах грунта полностью подчиняется закону Дарси.(см. вопрос)

 

73. Какие методы определения осадки приняты в расчетной практике?

Расчет осадок фундаментов имеет огромное практическое значение.

Все выше приведенные формулы (в вопросе 71) для определения осадки грунтовых оснований будут справедливы лишь для фазы уплотнения грунтов, т.е. необходимым условием применимости показанных ранее зависимостей для осадок будет: нач Р_{кр .}:

где: Р- действующая нагрузка на грунт; нач Р_кр- начальное критическое давление, при котором под фундаментом не возникают зоны предельного равновесия (зоны сдвигов).

 

Метод послойного элементарного суммирования заключается в том, что осадку грунта под действием нагрузки от сооружения определяют как сумму осадок элементарных слоев грунта такой толщины, для которых можно без большой погрешности принимать при расчетах средние значения действующих напряжений и средние значения характеризующих грунты коэффициентов.

В методе учитываются только осевые сжимающие напряжения по условию невозможности бокового расширения грунта. При определении осадок мысленно выделяют в грунте под центром подошвы фундамента вертикальную призму высотой от уровня подошвы до глубины активной зоны сжатия h_а

Метод эквивалентного слоя базируется на теории линейно деформируемых тел, но чрезвычайно упрощает технику вычислений как в случае однородных, так и слоистых напластований грунтов. Основные зависимости метода эквивалентного слоя предложены проф.Цытовичем Н.А. еще в 1934г. и в последующие годы (1940-1968) значительно усовершенствованы.

 

74.Коков принцип расчета по методу послойного элементарного суммирования?

Для различных сечений выделенной призмы (горизонтальных площадок) определяют по теории линейно деформируемых тел величину максимальных сжимающих напряже-ний σ_z. Далее считают, что каждый элемент грунта будет испытывать только вертикальное сжатие под действием среднего давления. Тогда для осадки будет применима формула (см. вопрос 71)

S=hm_vσ_z или

а для всей толщи

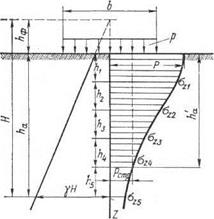где: h_i –мощность отдельных слоев грунта,

βi –коэффициент, зависящий от бокового расширения грунта (принимаемый по СНиП II-15-74 равным 0,8),(см. вопрос 81).

E_0i- модуль общей деформации грунта.

Знак суммы распространяется на всю глубину активной зоны сжатия h_a

Глубина активной зоны сжатия h_a соответствует такой глубине, ниже которой деформациями грунтовой толщи можно пренебречь. По СНиП II-15-74 эта глубина должна удовлетворять условию

 

75.Коков принцип расчета осадки по методу эквивалентного слоя?

Метод эквивалентного слоя грунта, так же как и все предыдущие методы расчета осадок фундаментов, базируется на теории линейно деформируемых тел.

Для однородных на достаточную глубину грунтов определение полной стабилизи-рованной осадки фундаментов по методу эквивалентного слоя является строгим реше-нием теории уплотнения линейно деформируемого полупространства (см. вопрос 71).

,

где: h_э -мощность эквивалентного слоя равная:

коэффициент А зависит от бокового расширения грунта μ₀

коэффициент -зависит от формы и жескости фундамента и пропорционален ширине подошвы b.

Для определения h_э -мощности эквивалентного слоя, т.е. А составлены таблицы в зависимости от вида грунта, соотношения = α и μ₀ (книга Н.А.Цытовича, стр. 204)

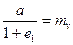-коэффициент относительной сжимаемости

P- напряжения под подошвой фундамента (σ_z)

Для определения осадок с прямоугольной площадью подошвы пользуются методом угловых точек.

76. Как изменится основная формула определения осадки по методу эквивалентного слоя для фундамента с круглой формой подошвы?

Для фундамента с круглой формой подошвы без большой погрешности пользуются следующим соотношением

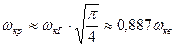
где ω_кр- коэффициент формы для фундамента с круглой площадью подошвы

ω_кв- то же, для фундамента с квадратной площадью подошвы(при α = =1).

Таким образом h_э -мощность эквивалентного слоя равная: .

и, как и для прямоугольного фундамента, по формуле определяют осадку.

 

77. Каков принцип расчета осадки по методу угловых точек?

Для определения осадки фундамента прямоугольной формы подошвы под любой точкой необходимо рассматриваемую точку расположить так, чтобы она была угловой.

Здесь следует рассмотреть три основных случая:

1) точка М₁ (а) лежит на контуре загруженного прямоугольника;

2) точка М₂ (б) лежит внутри загруженного прямоугольника;

3) точка М₃ (в) лежит вне загруженного прямоугольника.

В первом случае осадка точки М₁ определится как сумма осадок угловых точек прямоугольников I и II, т.е.

где ;

Во втором случае загруженную площадь разбивают на четыре прямоугольника так, чтобы точка М₂ была угловой и тогда

где -толщина эквивалентного слоя для соответствующих площадей загрузки.

В третьем случае поступают аналогично, т.е. осадка складывается из алгебраической суммы осадок угловых точек прямоугольников загрузки.

 

78. Что называется "осадочным" давлением и какое обосно­вание дается тому, что осадка рассчитывается не на полную величину давления?

Осадочным давлением р_о именуется разность давлений полного передаваемого основанию через подошву фундамента и "бытового" -природного давления, которое испытывает грунт на отметке заложения подошвы фундамента. Таким образом, осадка рассчитывается не на полную величину прикладываемого давления, а на уменьшенную. Обоснованием для этого служит то, что осадки в грунтовом массиве от веса вышележащей толщи уже завершились, а упругие деформации подъема незначительны, также как и повторные осадки (упругие и остаточные) при нагрузке в пределах давления от вышележащей толщи грунта. Поэтому кривая "осадка-нагрузка" будет иметь вид, показанный на рис.

а - нагрузка - полная разгрузка и вторичная нагрузка; б - условная схема, принимаемая в -методе элементарного суммирования для расчета осадок

79. Какие основные допущения заложены в расчете осадки способом послойного суммирования?

Основные допущения следующие:

1. Осадка происходит только при давлениях, превышающих природное давление на отметке заложения подошвы фундамента.

2. Связь между давлением и относительной деформацией линейная и может быть описана зависимостью закона Гука,

3. Напряжения в грунтовом массиве распределяются в соответствии с решениями теории упругости.

4. Рассчитывается эпюра давлений σ_z по глубине только по оси симметрии нагрузки (x = 0), и эти напряжения считаются одинаковыми вдоль горизонтальной оси х. Таким образом, имеет место некоторое завышение напряжений, действующих вдоль оси х, против средних значений в пределах ширины подошвы фундамента.

5. Считается, что грунт не претерпевает бокового расширения и сжимается только в вертикальном направлении (за счет этого осадка несколько преуменьшается). Схема показана на рис.

 

Схема для расчета осадок по методу послойного элементарного суммирования

1.-Элементарный слой до деформации;

2..-то же, после деформации.

 

80. От какого горизонта отсчитывается эпюра природного давления?

Эпюра природного давления отсчитывается от отметки поверхности грунта-от природного рельефа.

 

81. Какими принимаются боковые давления при расчете осадки способом послойного суммирования? Можно ли считать, что боковое расширение грунта в этом способе полностью не учитывается?

При расчете осадки способом послойного суммирования боковые деления принимаются такими, какими они получаются при сжатии грунта в одометре, то есть

Хотя при расчете осадок боковое расширение грунта в этом способе и не учитывается

(принимается, что боковые деформации равны нулю), но косвенно они учитываются тем, что распределение напряжений получено из решения теории упругости для полупрост-ранства (или полуплоскости), в котором считалось, что среда имела возможность боковых перемещений. Таким образом, оно непосредственно не учитывается, а косвенно и частично учтено.

 

82. В формуле расчета осадки способом послойного суммирования имеется коэффициент β. От чего он зависит?

Коэффициент β определяется из выражения:

и, следовательно, зависит только от коэффициента Пуассона грунта μ₀ (коэффициента относительной поперечной деформации). В СНиП 2.02.01-83 условно принято постоянное значение для β (считается, что β = 0,8).

83. В каких пределах ведется суммирование осадки при расчете методом послойного суммирования?

Всегда ли принимается при определении положения нижней границы сжимаемой толщи коэффициент 0,2?

В методе послойного суммирования осадки суммируются до той отметки, когда осевые дополнительные по отношению к природным напряжения не снизятся до 20 % от природных (бытовых) на этой же отметке. Эта отметка считается нижней границей сжимаемой толщи (B.C.), а осадками за счет сжатия нижерасположенной толщи пренебрегают. Однако, если ниже расположены слабые грунты с модулем деформации Е < 5 МПа, то нижнюю границу сжимаемой толщи следует опустить до той отметки, где дополнительные по отношению к природным давления составят 10 % от природных, а не 20 % как обычно.

 

84. Получается ли линейная зависимость осадки от нагрузки в методе послойного суммирования?

Нет, не получается в связи с тем, что положение нижней границы сжимаемой толщи изменяется в зависимости от действующего сверху осадочного давления - чем больше осадочное давление, тем ниже при прочих равных условиях будет положение нижней границы сжимаемой толщи. Поэтому зависимость осадки от нагрузки не будет линейной.

85.От каких факторов зависит положение нижней границы сжимаемой толщи в методе послойного суммирования (будет ли она располагаться ниже или выше)?

Зависит от:

- плотности грунтов основания;

- наличия горизонта грунтовых вод;

- заглубления фундамента;

- нагрузки на фундамент;

- ширины фундамента;

- соотношения сторон подошвы фундамента в плане;

- наличия слоя слабого грунта в основании.

86. Каким образом влияют расположенные рядом фундаменты друг на друга? Как строится эпюра напряжений σ_z при наличии расположенного рядом фундамента? Как поступить, если подошвы соседних фундаментов расположены в разных уровнях?

При расположении фундаментов рядом наличие одного из них влияет на осадку соседнего фундамента. Это обстоятельство следует учитывать при расчете осадки (рис.). Поэтому кдополнительным давлениям σ_z, рассчитываемого фундамента следует добавить значения напряжений σ_z, возникающих в этом месте от соседнего фундамента, пользуясь способом угловых точек. Если отметки подошвы одного и другого фундаментов одинаковы, то эпюра дополнительных давлений будет иметь нулевую ординату вверху. Если соседний фундамент 2 имеет более высоко расположенную подошву, то эпюра получит в уровне подошвы рассчитываемого фундамента 1 конечное значение дополнительного от соседнего фундамента 2 давления Δσ_z.

 

 

 

а) б)

Схемы для расчета осадок при наличии близко расположенных фундаментов:

а)- фундаменты 1 и 2 находятся рядом на одном уровне;

б)- фундамент 2 расположен выше, чем фундамент 1

87. Для какого случая получено решение задачи об осадке фундамента, в котором учитывается влияние всех компонентов напряжений?

Для однородного изотропного грунта, у которого и модуль деформации Е₀ и коэффициент Пуассона μ₀ постоянны.

88. Как вычислить значения модуля деформации грунта Ео_г необходимые для расчета осадки, по результатам штамповых испытаний в поле или компрессионных испытаний в одометре?

На кривой "осадка-нагрузка" штампа выбираются две точки, в пределах которых ведется спрямление. Рекомендуется, чтобы первая точка соответствовала бы давлению в грунте в точке отбора образца от собственного веса вышележащих слоев Р₁, а вторая соответствовала бы полному давлению Р₂ от веса грунта иожидаемой нагрузки от сооружения. Имеется в виду, что кривая в диапазоне выбранных двух давлений хорошо бы аппроксимировалась прямой. Для вычисления модуля деформации Ео, МПа, используется формула

 

Здесь S₂ и S₁ - см –величины осадки, соответствующие давлениям Р₁ и Р₂,МПа; d –диаметр штампа, см; ω- коэффициент формы штампа, равный 0,85; μ₀ - коэффициент Пуассона грунта, принимаемый обычно 0,3 для песков и супесей и 0,4 для глин. По результатам компрессионных испытаний в одометре величина Е₀,МПа, вычисляется по формуле:

Где е₁ и е₂ - значения коэф. пористости, соответствующие давлениям р₁ и р₂

е₀ –начальный коэф. пористости.

 

а)штамповые испытания; б) компрессионные испытания

 

89. Когда рекомендуется применять способ расчета осадки с использованием расчетной схемы в виде линейно-деформируемого слоя конечной толщины?

Этим способом предлагается пользоваться; еслимодуль деформации грунта основания более 100 МПа или если модуль деформации Е_о > 10 МПа; но ширина подошвы фундамента более 10 м. В этом случае осадочное давление считается равным полному.

90. Почему в формулу осадки для жесткого штампа на упругом полупространстве не входит глубина сжимаемой толщи?

Потому, что полупространство снизу не ограничено (толщина равна бесконечности) и при решении задачи отыскивается несобственный интеграл. Если бы толщина была ограничена конечным размером, она входила бы в окончательную формулу осадки.

91. От каких факторов зависит коэффициент ω в формуле осадки для полупространства? Чему он равен для круга, квадрата, "ленты"?

Этот коэффициент зависит от формы в плане загруженной площадки (квадрат, круг, прямоугольник), а также от жесткости штампа (гибкий штамп или жесткий). Для круга и жесткого штампа он равен 0,79, для квадрата - 0,88, для "ленты" (соотношение размеров сторон 10:1 и более) - 2,12.

 

92. С чем связано то обстоятельство, что грунты деформируются не сразу после приложения нагрузки, а на это требуется определённое время?

Это связано с тем, что деформация грунта определяется изменением его пористости и для деформирования грунта нужно деформирование междучастичных связей. Эти связи часто бывают вязко-пластичными и деформируются не сразу, а с течением времени. Кроме того, в порах грунта содержится вода и изменение пористости, особенно полностью водонасыщенного грунта, связано с необходимостью отжатая воды из пор грунта, на что требуется время.

 

93. С какой скоростью в твердых телах распространяются напряжения?

В твердых телах напряжения распространяются со скоростью звука.

 

94. Какой представляется модель полностью водонасыщенного глинистого грунта? Что моделирует диаметр отверстий в поршне?

К. Терцаги предложил для полностью водонасыщенного глинистого грунта такую модель: цилиндр, заполненный водой, внутри которого имеется стальная пружина. Цилиндр закрыт поршнем, имеющим весьма малые отверстия. Если на этот поршень поставить груз, то опускание поршня возможно только за счет выдавливания из цилиндра лишней воды. Поршень начнет надавливать на пружину и остановится лишь тогда, когда все усилия груза полностью передадутся на пружину. При этом лишняя вода из цилиндра выдавится наружу. Диаметр отверстий моделирует фильтрационную способность грунта - чем мельче отверстия, тем медленнее выдавливается вода и медленнее идет процесс осадки.(см. рис.)

 

 

95. В чем заключаются предпосылки теории фильтрационной консолидации? Что представляет собою степень консолидации, на что она указывает, в каких пределах изменяется и какова ее размерность?

Предпосылки теории фильтрационной консолидации сводятся к следующему:

- скелет грунта линейно-деформируемый, деформируется мгновенно после приложения к нему нагрузки и вязкими связями не обладает;

- структурной прочностью грунт не обладает, давление в первый момент полностью передается на воду;

- грунт полностью водонасыщен, вода и скелет объемно несжимаемы, вся вода в грунте гидравлически непрерывна;

- фильтрация подчиняется закону Дарси.

Степень консолидации U указывает на то, какая часть полной осадкипроизошла к данному моменту времени. Степень консолидации безразмерна и изменяется от нуля (при t = 0) до единицы (при t = ∞).

-

96. Какие напряжения вызывают сжатие грунта?

Только эффективные, то есть передающиеся на скелет грунта. Нейтральное давление на сжатие грунта не влияет.

97. Какие случаи изменения полного давления (эпюры напряжений σ_z) рассмотрены на практике и являются типовыми?

Рассмотрены три случая:

1) эпюра прямоугольная;

2) эпюра треугольная с вершиной вверху, у границы (имеется ввиду сжатие грунта от собственного веса);

3) эпюра треугольная с вершиной внизу и конечной ординатой вверху (эта эпюра соответствует способу эквивалентного слоя).

 

98. Какой порядок имеет уравнение фильтрационной консолидации и к какому типу дифференциальных уравнений оно принадлежит?

Уравнение Фурье линейное, второго порядка и параболического типа. Оно является уравнением, описывающим нестационарный процесс, так как содержит время.

 

99. В чем состоит метод Фурье решения уравнения теории фильтрационной консолидации?

Метод Фурье состоит в следующем. Поскольку основное уравнение линейное и содержит два переменных аргумента (координаты и время), то решением его будет сумма частных решений. Частные решения отыскиваются в виде произведения двух неизвестных функций - одной от координаты, другой от времени. В результате мы получаем уравнение, распадающееся на два обыкновенных дифференциальных уравнения, которые легко интегрируются. Дальнейшая задача связана с определением постоянных интегрирования исходя из граничных и начального условий.

 

100. Каким образом следует вести расчет по теории фильтрационной консолидации, чтобы воспользоваться готовыми таблицами?

Следует найти, задаваясь степенью консолидации U, по таблице величину фактора времени N и далее по формуле найти соответствующую величину времени t. Таким образом вычисления сильно упрощаются.

 

 

Галашев Ю.В. Скибин Г.М.