Означення неперервності функцій
|
 визначена в точці
визначена в точці  і деякому околі, що містить точку
і деякому околі, що містить точку  . Знайдемо значення функції в точці
. Знайдемо значення функції в точці  , яке позначимо
, яке позначимо 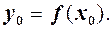 Далі, надамо значенню
Далі, надамо значенню  приріст
приріст  , тобто знайдемо нове значення
, тобто знайдемо нове значення  , де приріст
, де приріст  може бути як додатним (тоді
може бути як додатним (тоді  лежить правіше
лежить правіше  ), так і від’ємним (тоді
), так і від’ємним (тоді  знаходиться лівіше
знаходиться лівіше  ). Тепер обчислимо нове значення функції
). Тепер обчислимо нове значення функції  і знайдемо різницю між
і знайдемо різницю між  і
і 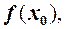 яку позначимо через
яку позначимо через  , тобто (див. рис. 28),
, тобто (див. рис. 28), 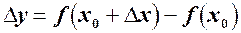 .
.
Рис. 28.
Означення 1. Функція  називається неперервною в точці
називається неперервною в точці  , якщо вона визначена в точці
, якщо вона визначена в точці  , а також в деякому околі цієї точки, і якщо н.м. приросту аргумента
, а також в деякому околі цієї точки, і якщо н.м. приросту аргумента  відповідає н.м. приріст функції
відповідає н.м. приріст функції  , тобто
, тобто
 , (1)
, (1)
або рівносильне цьому
 (2)
(2)
Перетворимо рівність (2)

Оскільки 
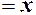 , то
, то  , і крім того,
, і крім того,
 (
( стала!), то далі маємо
стала!), то далі маємо

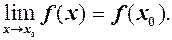 (3)
(3)
Отже, якщо функція неперервна в точці  , то границя функції дорівнює значенню цієї функції в точці
, то границя функції дорівнює значенню цієї функції в точці  . Якщо ж врахувати, що
. Якщо ж врахувати, що  , то рівність (3) запишеться
, то рівність (3) запишеться
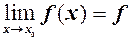
 (4)
(4)
Рівність (4) означає, що для неперервної функції  можна переходити до границі під знаком функції.
можна переходити до границі під знаком функції.
Довести, що функції 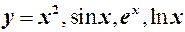 є неперервними в довільній точці
є неперервними в довільній точці  .
.
1. Нехай  . Тоді для
. Тоді для  знаходимо
знаходимо 
 .
.
Звідки знаходимо

Із  неперервна функція для
неперервна функція для 
Аналогічно можна довести, що неперервними є функції 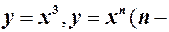 натуральне).
натуральне).
2. Нехай  .
.
Подібно попередньому для 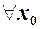 знаходимо
знаходимо  ,
,
 при
при  .
.
3. Нехай  .
.
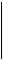
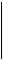 Для
Для 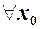 маємо
маємо 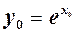 ,
, 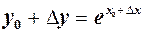
 див. формулу 8 таблиці»
див. формулу 8 таблиці»
еквівалентних із 3.12
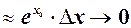 , при
, при  .
.
4. Нехай 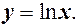
Для 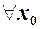



 » Див. формулу 7 із 3.12. таблиці
» Див. формулу 7 із 3.12. таблиці  .
.
еквівалентних н.м.
Отже,  неперервна функція для
неперервна функція для 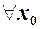
 . Враховуючи (4), можна сказати, що
. Враховуючи (4), можна сказати, що

це і було використано в 3.12 при доведенні формули (1).
Подібним чином можна довести неперервність решти основних елементарних функцій в довільній точці  , де ці функціїї визначені.
, де ці функціїї визначені.
Означення 2. Якщо функція  неперервна в кожній точці деякого інтервалу
неперервна в кожній точці деякого інтервалу  , де
, де  , то кажуть, що функція неперервна на цьому інтервалі.
, то кажуть, що функція неперервна на цьому інтервалі.
Якщо функція  визначена в точці
визначена в точці  і при цьому
і при цьому  , то говорять, що
, то говорять, що  неперервна справа в точці
неперервна справа в точці  . Якщо
. Якщо 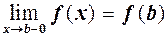 , то говорять, що
, то говорять, що  неперервна зліва в точці
неперервна зліва в точці  .
.
Якщо функція  неперервна на інтервалі
неперервна на інтервалі  і неперервна на кінцях цього інтервала, відповідно справа і зліва, то говорять, що функція
і неперервна на кінцях цього інтервала, відповідно справа і зліва, то говорять, що функція  неперервна на всьому відрізку
неперервна на всьому відрізку 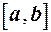 .
.
Наведемо без доведення наступну теорему.
Теорема. Всяка елементарна функція неперервна в кожній точці, в якій вона визначена.
Розривні функції. Види розривів
Якщо в якійсь точці 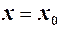 для функції
для функції  не виконується хоча б одна із умов неперервності, тобто якщо в точці
не виконується хоча б одна із умов неперервності, тобто якщо в точці 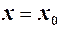 функція невизначена, або неіснує границя
функція невизначена, або неіснує границя 
 , або
, або  при довільному прямуванні
при довільному прямуванні  , хоча вирази
, хоча вирази  і
і  існують, то при
існують, то при 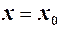 функція
функція  розривна. Точка
розривна. Точка 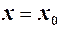 називається точкою розриву функції.
називається точкою розриву функції.
Розрізняють такі три види розривів:
1) усувний розрив;
2) розрив І-го роду або скінченний розрив;
3) розрив ІІ-го роду або нескінченний розрив.
Якщо функція  в деякому околі точки
в деякому околі точки 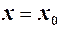 визначена і її односторонні границі збігаються, тобто
визначена і її односторонні границі збігаються, тобто
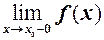 =
=  ,
,
а в самій точці 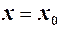 функція невизначена, то в цій точці
функція невизначена, то в цій точці  має усувний розрив. Цей розрив можна усунути, приписавши функції значення, що збігається з односторонніми границями і взявши
має усувний розрив. Цей розрив можна усунути, приписавши функції значення, що збігається з односторонніми границями і взявши

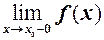 =
=  .
.
Наприклад, функція  неперервна на всьому інтервалі від –¥ до +¥, крім точки
неперервна на всьому інтервалі від –¥ до +¥, крім точки  . В точці
. В точці  функція
функція  розривна.
розривна.
Розглянемо нову функцію 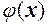 , таку, що
, таку, що  якщо
якщо
 , а при
, а при  покладемо
покладемо 
Побудована таким чином функція
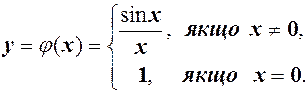
є неперервною для  (див. рис. 29), тобто розрив усунули.
(див. рис. 29), тобто розрив усунули.

Рис. 29.
Якщо односторонні границі функції  скінченні при
скінченні при  і
і  , то функція в точці
, то функція в точці 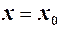 має розрив І-го роду або скінченний розрив.
має розрив І-го роду або скінченний розрив.
Наприклад, функція  при
при  дорівнює
дорівнює  при
при 
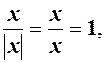 а при
а при  функція невизначена, тоді
функція невизначена, тоді


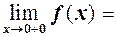

отже  має розрив І-го роду (див. рис. 30).
має розрив І-го роду (див. рис. 30).

Рис. 30.
Стрибком функції  називається величина
називається величина



У точках неперервності стрибок  , для розривів І-го роду він скінченний. Для розглянутого на рис. 30 графіка стрибок
, для розривів І-го роду він скінченний. Для розглянутого на рис. 30 графіка стрибок  .
.
Якщо хоча б одна з односторонніх границь функції  в точці
в точці 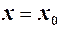 є нескінченною або не існує, тоді функція в точці
є нескінченною або не існує, тоді функція в точці 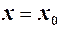 має розрив ІІ-го роду або нескінченний розрив.
має розрив ІІ-го роду або нескінченний розрив.
Наприклад, 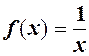 в точці
в точці  невизначена,
невизначена,  , а
, а  , тобто односторонні границі нескінченні, тому тут розрив ІІ-го роду (див. рис.31).
, тобто односторонні границі нескінченні, тому тут розрив ІІ-го роду (див. рис.31).
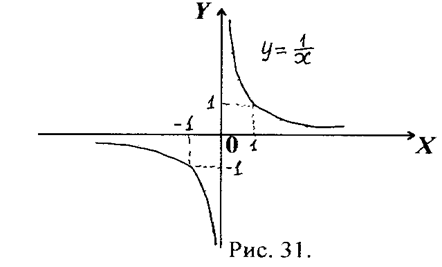
Так само точка  є точкою розриву ІІ-го роду для розглянутої раніше функції
є точкою розриву ІІ-го роду для розглянутої раніше функції  , бо
, бо  не існує.
не існує.







