Модели вычислений: Машина Тьюринга, РАСП, РАМ, неветвящиеся программы, деревья решений

 

Тренажёр «Машина Тьюринга» — это учебная модель универсального исполнителя (абстрактной вычислительной машины), предложенного в 1936 году А. Тьюрингом для уточнения понятия алгоритма. Согласно тезису Тьюринга, любой алгоритм может быть записан в виде программы для машины Тьюринга. Доказано, что машина Тьюринга по своим возможностям эквивалентна машине Поста и нормальным алгорифмам Маркова.

Машина Тьюринга (МТ) – это математическая модель идеализированной цифровой вычислительной машины.

Машина Тьюринга является таким же математическим объектом, как функция, производная, интеграл, группа и т. д. Так же как и другие математические понятия, понятие машины Тьюринга отражает объективную реальность, моделирует некие реальные процессы. Для описания алгоритма МТ удобно представлять некоторое устройство, состоящее из четырех частей: ленты, считывающей головки, устройства управления и внутренней памяти.

1. Лента предполагается потенциально бесконечной, разбитой на ячейки (равные клетки). При необходимости к первой или последней клетке, в которой находятся символы пристраивается пустая клетка. Машина работает во времени, которое считается дискретным, и его моменты занумерованы 1, 2, 3, …. В каждый момент лента содержит конечное число клеток. В клетки в дискретный момент времени может быть записан только один символ (буква) из внешнего алфавита A = {L, 1 2 1,,..., a a an-}, n ³ 2.

Пустая ячейка обозначается символом L, а сам символ L называется пустым, при этом остальные символы называются непустыми. В этом алфавите A в виде слова (конечного упорядоченного набора символов) кодируется та информация, которая подается в МТ. Машина «перерабатывает» информацию, поданную в виде слова, в новое слово.

2. Считывающая головка (некоторый считывающий элемент) перемещается вдоль ленты так, что в каждый момент времени она обозревает ровно одну ячейку ленты. Головка может считывать содержимое ячейки и записывать в нее новый символ из алфавита А. В одном такте работы она может сдвигаться только на одну ячейку вправо (П), влево (Л) или оста- ваться на месте (Н). Обозначим множество перемещений (сдвига) головки D = {П, Л, Н}. Если в данный момент времени t головка находится в край ней клетке и сдвигается в отсутствующую клетку, то пристраивается новая пустая клетка, над которой окажется головка в момент t +1.

3. Внутренняя память машины представляет собой некоторое конеч-ное множество внутренних состояний Q = { q0, q1, q2,..., qm}, m ³ 1. Будем считать, что мощность |Q | ³ 2. Два состояния машины имеют особое значение: q1 – начальное внутреннее состояние (начальных внутренних состояний может быть несколько), q0 – заключительное состояние или стоп-состояние (заключительное состояние всегда одно). В каждый момент времени МТ характеризуется положением головки и внутренним состоянием. Например, под ячейкой, над которой находится головка, указывается внутреннее состояние машины.

Ø a2 a1 L a2 a3 q1

4. Устройство управления в каждый момент t в зависимости от считываемого в этот момент символа на ленте и внутреннего состояния машины выполняет следующие действия: 1) изменяет считываемый в момент t символ ai на новый символ a j (в частности оставляет его без изменений, т. е. ai = a j);

2) передвигает головку в одном из следующих направлений: Н, Л, П; 3) изменяет имеющееся в момент t внутреннее состояние машины9 qi на новое q j, в котором будет машина в момент времени t +1 (может быть, что qi = q j).

Такие действия устройства управления называют командой, которую можно записать в виде:

qiai a j D q j Æ, (1)

где qi – внутреннее состояние машины в данный момент; ai – считываемый в этот момент символ; a j – символ, на который изменяется символ ai (может быть ai = a j); символ D есть или Н, или Л, или П и указывает направление движения головки; q j – внутреннее состояние машины в следующий момент (может быть qi = q j). Выражения qiai и a j D q j называются левой и правой частями этой команды соответственно. Число команд, в которых левые части попарно различ- ны, является конечным числом, так как множества \ { } Q q0 и A конечны. Не существует команд с одинаковыми левыми частями, т. е. если программа машины T содержит выражения qiai a j D q j Æ и t t k k q a Æ a D q, то qi ¹ qt или ai ¹ at и DŒ{П, Л, Н}. Совокупность всех команд называется программой машины Тьюринга. Максимальное число команд в программе равно (n +1) × m, где n +1= A и m +1= Q. Считается, что заключительное состояние команды q0 может стоять только в правой части команды, начальное состояние q1 может стоять как в левой так и в правой части команды.

Выполнение одной команды называется шагом. Вычисление (или работа) машины Тьюринга является последовательностью шагов одного за другим без пропусков, начиная с первого. Итак, МТ задана, если известны четыре конечных множества: внешний алфавит A, внутренний алфавит Q, множество D перемещений головки и программа машины, представляющая собой конечное множество команд

 

В 1936 г. Аланом Тьюрингом для уточнения понятия алгоритма был предложен абстрактный универсальный исполнитель. Его абстрактность заключается в том, что он представляет собой логическую вычислительную конструкцию, а не реальную вычислительную машину. Термин «универсальный исполнитель» говорит о том, что данный исполнитель может имитировать любой другой исполнитель. Например, операции, которые выполняют реальные вычислительные машины можно имитировать на универсальном исполнителе. В последствие, придуманная Тьюрингом вычислительная конструкция была названа машиной Тьюринга. Кроме того, предполагается, что универсальный исполнитель должен уметь доказывать существование или отсутствие алгоритма для той или иной задачи.

Что собой представляет машина Тьюринга?

Машина Тьюринга состоит из бесконечной в обе стороны ленты, разделенной на ячейки, и автомата (головки), которая управляется программой. Программы для машин Тьюринга записываются в виде таблицы, где первые столбец и строка содержат буквы внешнего алфавита и возможные внутренние состояния автомата (внутренний алфавит). Содержимое таблицы представляет собой команды для машины Тьюринга. Буква, которую считывает головка в ячейке (над которой она находится в данный момент), и внутренне состояние головки определяют, какую команду нужно выполнить. Команда определяется пересечением символов внешнего и внутреннего алфавитов в таблице.

Чтобы задать конкретную машину Тьюринга, требуется описать для нее следующие составляющие:

Внешний алфавит. Конечное множество (например, А), элементы которого называются буквами (символами). Одна из букв этого алфавита (например, а₀) должна представлять собой пустой символ.

Внутренний алфавит. Конечное множество состояний головки (автомата). Одно из состояний (например, q₁) должно быть начальным (запускающим программу). Еще одно из состояний (q₀) должно быть конечным (завершающим программу) – состояние останова.

Таблица переходов. Описание поведения автомата (головки) в зависимости от состояния и считанного символа.

Автомат машины Тьюринга в процессе своей работы может выполнять следующие действия:

Записывать символ внешнего алфавита в ячейку (в том числе и пустой), заменяя находившийся в ней (в том числе и пустой).

Передвигаться на одну ячейку влево или вправо.

Менять свое внутреннее состояние.

Одна команда для машины Тьюринга как раз и представляет собой конкретную комбинацию этих трех составляющих: указаний, какой символ записать в ячейку (над которой стоит автомат), куда передвинуться и в какое состояние перейти. Хотя команда может содержать и не все составляющие (например, не менять символ, не передвигаться или не менять внутреннего состояния).

Пример работы машины Тьюринга

Допустим, на ленте есть слово, состоящее из символов #, $, 1 и 0. Требуется заменить все символы # и $ на нули. В момент запуска головка находится над первой буквой слова слева. Завершается программа тогда, когда головка оказывается над пустым символом после самой правой буквы слова.
Примечание: длина слова и последовательность символов значения не имеют. На рисунке приводится пример последовательности выполнения команд для конкретного случая. Если на ленте будет другое слово, то и последовательность выполнения команд будет другой. Несмотря на это, данная программа для машины Тьюринга (на рисунке – таблица слева) применима к любым словам описанного внешнего алфавита (соблюдается свойство применимости алгоритма ко всем однотипным задачам – массовость).

 

Наиболее простой и наиболее изученной моделью является Машина Тьюринга (МТ).

Система команд МТ является очень простой и содержит простейшие команды добавления единицы, присваивания и очистки. С использованием этой модели были изучены сложностные аспекты и получены нижние и верхние оценки временной сложности для широкого класса задач. Однако программирование на языке МТ является достаточно неудобным и сложным, а главное – характер доступа к данным в языке МТ заметно отличается от имеющегося в современных ЭВМ. С этих позиций более близкими к современным ЭВМ являются RAM и RASP машины. RASP-модель (Random Access Stored Program) – машинас произвольным доступом к памяти и хранимой программой. Характерным для RASP– модели является то, что программа находится в памяти и может изменять себя. Эта модель реализует предельный случай, когда сняты ограничения на размер оперативной памяти компьютера и ограничения на размер чисел, помещаемых в этих ячейках. Но в процедурных языках программирования (изначально) не предусматриваются средства динамической (в периоде выполнения) модификации программ. Поэтому для такого программирования наиболее близкой является RAM модель (Random Access Machine) – машины с произвольным доступом к памяти. RAM-машина моделирует вычислительную машину с одним сумматором, при этом программа не может модифицировать саму себя. Команды этой машины напоминают команды ЭВМ, включают арифметические команды, команды адресации, присваивания, ввода – вывода_______, команды передачи управления по некоторому условию. Оперативная память неограниченна и состоит из бесконечного числа регистров, в которые записываются целые числа. Машина считывает данные из входной ленты, результаты работы записываются на выходную ленту. Программа RAM- машины состоит из последовательности помеченных команд, которые выполняются в заданном порядке, кроме случаев, определяемых командами условного перехода. Доказано, что вычислительные способности не сильно изменяются при переходе от одной модели к другой, сложностные оценки связаны между собой подходящими полиномами (небольшой степени). С учетом сказанного, при оценке времени работы программы (на обычном процедурном языке программирования) можно использовать следующее соглашение – время выполнения операторов присваивания, сравнения, ввода и вывода будем считать константой. При этом операторы могут содержать выражения, но с операциями базового типа 12. Точно определить некоторые константы пропорциональности нет возможности, поскольку они зависят от компилятора, компьютера и других факторов. Точное определение функции времени T(n) фактически обычно нас тоже не очень интересует, обычно она сложно представима, а нас скорее интересует возможность сравнивать алгоритмы по скорости роста соответствующих оценок времени. Для таких целей более удобны асимптотические представления функции времени. Эти функции разбиваются на классы эквивалентности в зависимости от скорости роста. По построенным классам эквивалентности для фиксированных моделей вычислений строятся сложностные иерархии, позволяющие классифицировать сложности решения соответствующих задач.

Деревья решений:

Деревья решений – это способ представления правил в иерархической, последовательной структуре, где каждому объекту соответствует единственный узел, дающий решение.

Дерево решений – это граф, представляющий правила в иерархической последовательной структуре, где каждому объекту соответствует единственный узел, дающий решение.

Дерево решений обычно строится следующим образом. Сначала берется весь набор данных, который представляется исходной или корневой вершиной. Затем определяются способы (правила) разбиения на ветви всего множества записей или вариантов, соответствующих корневому узлу. Ветви образуют дерево, повернутое кроной вниз. На ветвях дерева отмечают узлы, отвечающие подмножеству записей или вариантов. На каждом узле снова определяются правила разбиения на ветви и т.д. до тех пор, пока процесс не дойдет до конечных узлов, называемых листьями. В связи с этим, деревья решений часто применяются для моделирования (генерации) «многоэтапных» процессов принятия решений, в которых взаимосвязанные решения принимаются последовательно. Такое представление облегчает описание процесса принятия решений.

Правило или способы разбиения множеств записей или вариантов называют решающим правилом:

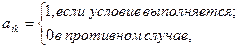
где 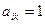, если условие 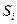для правила 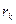выполняется;

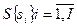- множество условий, описывающих параметры выбранной предметной области,

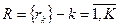- множество решающих правил, описывающих конкретные действия, выполняемых при заданных значениях параметров из множества условий.

Это правило фактически является логической структурой «если …, то …», делящее анализируемое множество на две группы. По мере спуска по дереву решений от вершины к листьям, создается все больше отфильтрованных однородных множеств, удовлетворяющих определенному набору условий, сформулированных в узлах дерева.

Для генерации различных вариантов решений и их оценки наибольшее распространение получили деревья решений, содержащие два типа вершин: вершины, в которых решение принимает эксперт (ЛПР) и вершины, где решение принимает «случай», выходящие из вершины дуги задают определенные вероятности направлений принятия решения.