Результатом виконання першої частини курсового проекту має бути визначення реакцій в кінематичних парах, та сил, що діють на окремі ланки механізму, за заданим рухом вхідної ланки. Розміри ланок механізму, положення центрів ваги, кутова швидкість провідної ланки, маси всіх ланок задаються умовами індивідуального завдання.
Для вивчення руху механізму потрібно знати його структуру: кількість ланок, кількість та класи кінематичних пар. Необхідними також є знання про взаємне розташування ланок. Тому першим етапом кінематичного аналізу є складання кінематичної схеми механізму. Її будують в обраному масштабі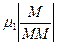 
, дотримуючись заданих розмірів та форм ланок. На кінематичній схемі мають бути відомості про все необхідне для вивчення руху. Кінематична схема механізму наведена в заданому положенні на рис. 6.1.
Рисунок 6.1 – Кінематична схема механізму
Визначити характер руху ланок механізму можна за допомогою плану положень. Будування плану починається з креслення нерухомих опор О, С. Далі будується траєкторія руху провідної ланки (коло) і на ній відмічають дванадцять положень ланки ОА через кожні 30о, починаючи з горизонтального правого положення, яке вважається першим. На наступному етапі викреслюються дві дуги з центрами в точках О та С, та радіусами 
та 
відповідно. Перетин дуг відповідає положенню точки В. На ланці ВС, відповідно заданому співвідношенню 
, знаходиться точка Д. Після цього будують дугу радіусом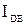 
з центром в точці Д. На перетині цієї дуги з горизонтальною напрямленою знаходиться точка Е. Ці будування необхідно провести для усіх дванадцяти положень провідної ланки.
Визначення швидкостей, прискорень точок та ланок механізму рекомендується проводити за допомогою методу планів. Побудова плану швидкостей починається з провідної ланки, оскільки задано, що її кутова швидкість 
– величина постійна. Лінійна швидкість точки А дорівнює
. (6.1)
Вектор швидкості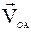 
перпендикулярний ланці у даному положенні та спрямований вздовж 
На площині креслення обирається полюс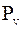 
і від нього проводиться вектор довільної довжини, який відповідає швидкості 
(рис. 6.2). Обчислюється масштабний коефіцієнт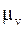 
за формулою:
(6.2)
де 
– швидкість точки А;
– довжина вектора на плані.
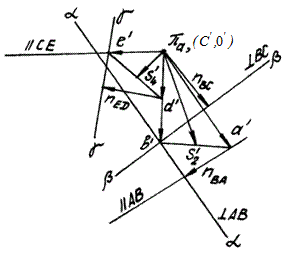
Рисунок 6.2 – Плани швидкостей та прискорень для заданого
положення механізму
Визначення швидкості точки В базується на належності цієї точки двом ланкам: АВ та ВС. Для плоскопаралельного руху, який виконують ці ланки, справедлива теорема про розподіл швидкостей: швидкість будь-якої точки тіла дорівнює векторній сумі швидкості полюса та відносній швидкості руху точки навколо полюса. Для ланки АВ зручно обрати полюсом точку А. Тоді швидкість точки В:
(6.3)
де 
– швидкість руху точки В навколо полюса А.
Аналогічне рівняння описує рух точки В відносно точки С:
(6.4)
де 
– швидкість точки С;
– відносна швидкість руху точки В навколо С.
Вектор швидкості точки В буде результатом спільного розв’язання двох векторних рівнянь (6.3) і (6.4). У рівнянні (6.3) перше складове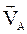 
відоме за величиною та напрямком, а про швидкість відомо лише те, що вона перпендикулярна ланці АВ. Тому для побудування векторної суми в околі точки а проводиться лінія, перпендикулярна АВ (рис. 6.2). У векторній сумі (6.2) перше складове – – дорівнює нулю, бо точка С нерухома. З полюса РV проводиться нульовий вектор. Другому складовому – – на плані швидкостей відповідатиме лінія, яка проходить крізь точку С перпендикулярно ланці ВС. На перетині ліній a-a та b-b знаходиться точка b. Вектор, що з¢єднує цю точку з полюсом, є аналогом швидкості 
. Абсолютне значення швидкості визначається за рівнянням:
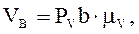(6.5)
де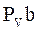 
– довжина вектора.
Ланка ВС виконує обертальний рух навколо точки С. Оскільки точка D належить цій ланці, для векторів швидкостей справедливо:
, (6.6)
де lDC – довжина ланки DС;
dc – довжина вектора на плані швидкостей.
На плані швидкостей точка d знаходиться на відрізку bс, розділяючи його у співвідношенні 
. Довжина вектора, що з¢єднує полюс з точкою d, відповідає швидкості 
, чисельне значення якої дорівнює
. (6.7)
Факт належності точки Е ланці DЕ дає векторне рівняння:
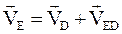. (6.8)
У цій векторній сумі невідоме друге складове - 
. Про нього відомо лише те, що лінія дії цього вектора перпендикулярна до ланки DЕ. Відповідну лінію необхідно провести на плані швидкостей крізь точку d. Щоб скласти друге рівняння для швидкості 
, на нерухомій напрямній необхідно виділити точку 
. Тоді швидкість 
дорівнюватиме
(6.9)
Швидкість точки Е0 дорівнює нулю, тому на плані точка е0 розміститься в полюсі. Швидкість 
спрямована вздовж напрямку руху повзуна. На плані цій швидкості відповідатиме лінія, яка паралельна напрямній (у нашому прикладі – горизонтальна) та проходить крізь точку е0. На перетині цієї лінії та лінії, що перпендикулярна ланці DЕ, знаходиться точка е.
Чисельно швидкість 
дорівнює
(6.10)
де 
– довжина вектора, що з¢єднує полюс з точкою е.
За допомогою плану швидкостей можна визначити кутові швидкості ланок механізму. Кутова швидкість ланки АВ:
, (6.11)
де lBA – довжина ланки;
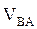– швидкість руху точки В відносно точки А. Її можна знайти, користуючись співвідношенням
, (6.12)
де ba – довжина відрізка, що з¢єднує точки a і b на плані швидкостей.
Аналогічно для ланки ВС:
(6.13)
для ланки DЕ:
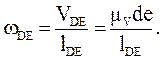(6.14)
Щоб знайти напрямок кутової швидкості 
, необхідно вектор 
умовно перенести в точку В. Вектор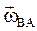 
буде спрямований у той же бік, що і . Таким же чином визначається напрямок векторів 
та 
.
Для визначення прискорень точок та ланок механізму використовується метод планів прискорень.
Побудування плану прискорень починається з провідної ланки. Задано, що 
, отже прискорення точки А:
, (6.15)
де 
– довжина ланки ОА.
Вектор прискорення точки А спрямований від неї до центру обертання, тобто до точки О, вздовж ланки. На площині креслення обирається полюс 
і від нього проводиться вектор довільної довжини паралельно ланці ОА. Кінець вектора позначається точкою а¢ (рис. 6.2). Обчислюється масштабний коефіцієнт:
(6.16)
де pа а¢ – довжина вектора на плані прискорень.
Прискорення точки В можна знайти з умови належності цієї точки двом ланкам: АВ та ВС. Обидві ланки виконують плоско-паралельний рух, для якого справедлива теорема про розподіл прискорень точок твердого тіла. Для ланки АВ полюсом краще обрати точку А, тоді прискорення точки В:
(6.17)
У цій векторній сумі перше складове відоме, друге – 
– спрямоване від точки В до точки А вздовж ланки і чисельно дорівнює
. (6.18)
Довжина відповідного відрізка на плані прискорень:
(6.19)
На плані прискорень з точки а¢ вздовж ланки АВ проводиться вектор довжиною nBA. Про третє складове векторного рівняння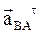 
відомий лише напрямок – перпендикулярний ланці. Тому на плані прискорень з кінця вектора 
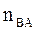навколо проводиться перпендикулярна лінія (рис. 6.2).
Належність точки В ланці ВС дає можливість записати рівняння:
(6.20)
Точка С є нерухомою, її прискорення дорівнює нулю, на плані точка с¢ розміщується в полюсі pа. Скалярне значення вектора 
визначається за співвідношенням:
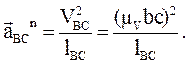(6.21)
Довжина вектора на плані прискорень:
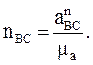(6.22)
До точки с¢ здобудовується вектор довжиною nBC, паралельний ланці ВС, а з його кінця навколо – перпендикуляри, які відповідають третій складовій векторного рівняння – 
. На перетині ліній a- a та b-b знаходиться точка b¢. Прискорення точки В дорівнює
(6.23)
де pа b¢ – довжина вектора, що з¢єднує полюс з точкою b¢.
Точку d¢ можна знайти на відрізку b¢с¢ відповідно до співвідношення:
, (6.24)
з якого:
. (6.25)
Значення прискорення aD визначається за формулою:
. (6.26)
Векторне рівняння плоско-паралельного руху ланки DЕ з полюсом в точці D:
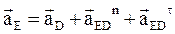, (6.27)
де 
– доцентрове прискорення руху точки Е відносно D;
– дотичне прискорення точки Е в її русі відносно точки D.
Доцентрове прискорення можна знайти таким чином:
, (6.28)
довжина відповідного вектора на плані:
(6.29)
На плані прискорень з точки d¢ проводимо вектор nDE, паралельний ланці DЕ та спрямований від Е до D, а з кінця цього вектора – перпендикуляр в обидва боки, який відповідає напрямку дотичного прискорення . Для дослідження руху повзуна необхідно використати точку Е0 на нерухомій напрямній. Тоді рівняння руху точки Е:
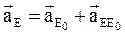. (6.30)
Оскільки точка Е0 нерухома, на плані прискорень точка е0¢ знаходиться в полюсі. Про прискорення 
відомо лише те, що воно паралельне напрямній. Тому на плані через точку е0¢ будується горизонтальна лінія. На перетині цієї лінії та лінії, яка перпендикулярна ланці DЕ, знаходиться точка е¢. Чисельне значення прискорення точки Е:
, (6.31)
де pа е¢ – довжина вектора, який з¢єднує полюс з точкою е¢.
Кутове прискорення ланки АВ можна визначити за співвідношенням:
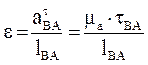, (6.32)
де tВА – довжина вектора на плані прискорень, який відповідає дотичному прискоренню 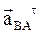. Якщо вектор 
умовно перенести в точку В, можна знайти напрямок eВА: вони спрямовані в один бік. Для визначення кутового прискорення ланок ВС та DЕ, використовуються такі співвідношення:
(6.33)
Їхні напрямки знаходять умовним перенесенням векторів 
та 
в точки В та Е відповідно.
Для визначення реакцій в кінематичних парах механізму необхідно розділити його на групи Асура. Таких груп дві – 
класу II порядку (ланки 2–3 та 4–5). Кінетостатичний аналіз починають з групи ланок, найбільш віддаленої від вхідної ланки.
Найбільш віддаленою групою Асура є група, що складається з ланок 4 та 5. Її необхідно викреслити в масштабі (рис. 6.3), шарнірні зв¢язки замінюються реакціями 
та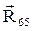 
, реакція в шарнірі D невідома ані за модулем, ані за напрямком, тому необхідно розкласти її на складові: за напрямком осі 
та перпендикулярно їй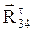 
; реакція в шарнірі E невідома за модулем і спрямована перпендикулярно осі Х.
Рисунок 6.3 – Структурна група 4–5 та многокутник сил, що діють на групу
Cума моментів відносно точки Е дорівнює нулю, тому модуль Rt34:
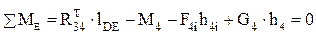, (6.34)
звідки
(6.35)
З рівняння рівноваги двоповідкової групи складається векторне рівняння
, (6.36)
в якому другий, третій та четвертий вектори відомі за модулем та напрямком, а перший та останній - лише за напрямком. Згідно з цим векторним рівнянням будується замкнений силовий многокутник. На площині креслення обирається полюс 
. Від нього проводять вектор довільної довжини у напрямку однієї з сил, що діють на групу (наприклад, 
). Далі необхідно обчислити масштабний коефіцієнт 
за співвідношенням:
(6.37)
де 
– довжина відповідного вектора на плані сил.
Після цього до вектора добудовують у довільному порядку інші складові з рівняння (6.36), перераховуючи довжини векторів за допомогою масштабного коефіцієнта. До початку вектора (точка 
) добудовується вектор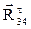 
, стрілка якого має бути спрямована на початок вектора (рис. 6.3). До початку вектора 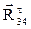добудовується лінія дії сили 
.
В точці перетину лінії з лінією дії 
закінчується вектор і починається вектор 
. Вектор можна отримати, з¢єднуючи початок вектора 
з кінцем 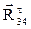. Цей вектор – результуюча сила в парі D. Для визначення реакції в обертальній парі Е (внутрішній парі групи), необхідно розглянути рівновагу ланки 4 або 5.
Векторне рівняння для рівноваги ланки 5:
(6.38)
Згідно з цим рівнянням будується силовий многокутник. У довільному масштабі послідовно відкладаються вектори 
та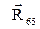 
. З¢єднавши кінці вектора 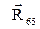з початком вектора можна отримати вектор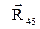 
результуючої сили в шарнірі Е (рис. 6.4).
Рисунок 6.4 – Силовий многокутник для ланки 5
Для силового розрахунку двоповідкової групи 2-3 до шарніра D (рис.6.5) необхідно прикласти силу 
, що за модулем дорівнює силі 
та протилежно їй спрямована. Вона є впливом відсутніх ланок 4 та 5.
Рисунок 6.5 – Структурна група 2–3 та многокутник сил, що діють на неї
Реакції в шарнірах А, В, та С не відомі ані за напрямком, ані за величиною. Відома лише точка прикладання цих сил – центр шарніра. Необхідно розкласти реакції в шарнірах А і С двоповодкової групи АВС на складові за напрямками осей 
та 
, та за напрямками, що їм перпендикулярні: 
, 
. Тангенційні складові можна знайти, якщо записати рівняння сум моментів кожної ланки відносно точки В.
Умова рівноваги ланки 2:
, (6.39)
звідки
(6.40)
Умова рівноваги ланки 3:
, (6.41)
звідки
(6.42)
Розглянувши рівняння рівноваги двоповідкової групи в цілому, можна побачити, що невідомі дві сили – та . На шарнір B діють дві сили 
та 
, які однакові за величиною, але протилежні за напрямком. Вони не входять до рівняння рівноваги всієї групи. Тому векторне рівняння рівноваги цієї групи матиме вигляд:
. (6.43)
В цьому рівнянні другий, третій, четвертий та шостий доданки відомі за модулем та напрямком, а перший та п¢ятий – лише за напрямком. Згідно з цим векторним рівнянням необхідно побудувати замкнений силовий многокутник, відкладаючи в обраному масштабі послідовно вектори сил та обходячи контур групи зліва направо від полюса (точка Р на рис.6.5).
Реакцію в шарнірі В (внутрішньої пари) можна визначити з плану cил, який побудовано за векторним рівнянням рівноваги для ланки 2 або 3:
(6.44)
або
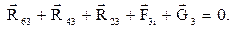(6.45)
Реакції в шарнірах знайдено.
Визначення урівноважувальної сили та урівноважувального моменту. На кривошип ОА діє шатун з силою 
. Для визначення урівноважувальної сили 
необхідно задатися її напрямком. Вважається, що силу прикладено перпендикулярно ланці ОА (рис. 6.6).
Рисунок 6.6 – Провідна ланка та сили, що діють на неї
В цьому випадку рівняння моментів усіх сил, які прикладено до кривошипу, відносно точки О матиме вигляд
, (6.46)
звідки
(6.47)
та урівноважувальний момент дорівнюватиме
. (6.48)
Реакцію в шарнірі О можна знайти графічним методом за допомогою векторного рівняння рівноваги сил
(6.49)
Для цього в обраному масштабі сил (рис. 6.7) необхідно послідовно відкласти сили 
. Із замкненого силового многокутника реакція в шарнірі О (
) визначається відрізком 1–4.
Рисунок 6.7 – Многокутник сил, що діють на провідну ланку
Графічну частину 1-го розділу курсового проекту подано на аркуші формату А1 (Додаток Д).
