Основные теоретические сведения. В лабораторной работе №7 был затронут вопрос, уменьшения пгрешности расчета при вычислении определенного интеграла от функции

 

В лабораторной работе №7 был затронут вопрос, уменьшения пгрешности расчета при вычислении определенного интеграла от функции . В ходе решения типовой задачи №2, были получены зависимости (рис. 23), позволяющие с определенной погрешностью найти значение интеграла на отрезке [0, x ]. Так для 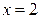методы правых и левых прямоугольников дали соотетственно значения 3.6 и 4.4. Из рис. 24 видно, что в обоих случаях погрешность определяется величиной суммарной площади криволинейных треуголников abe и bfg. Чем больше интервал интегрирования, тем больше суммарная площадь и, следовательно, погрешность вычисления.

 

Рис. 24

 

Очевидно, что добиться уменьшения площади треугольноков можно путем уменьшения по оси 0X размеров прямоугольнов abcd и bghc. При этом суммарная площадь треугольников, определяющая погрешность, существенно уменьшается.

Итак, теперь мы знаем, как повысить точность вычисления в принципе. Но как повысить точность до заданного уровня?

Общий алгоритм при решении подобных задач заключается следующем.

Шаг 1. Получают первое приближение искомой величины. В нашем случае мы можем разбить весь интервал интегрирования, например, на 10 участков и посчитать искомую площадь по 10 прямоугольникам.

Шаг 2. Получают следующее приблежение искомой величины с повышенной точностью. Мы уже знаем, что повысить точность можно, уменьшая размеры прямоугольников или, иными словами, увеличивая их количество. Для простоты можно принять, что при каждом последующем приближении, количество отрезков (примоугольников) на который разбивается исходный интервал, удваивается.

Шаг 3. Абсолютная разница между двумя последними приближениями искомой величины сравнивается с заданной точностью δ. Если разница меньше δ — вычисления завершаются. Если разница больше δ — повторяется шаг 2.

Подобный подход применим не только при вычислении определеных интегралов с заданной точностью. Его можно использовать для вычисления с заданной точностью любой величины, при условии, что мы можем влиять на точность вычисления.

Допустим нам необходимо рассчитать с точностью 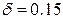сумму ряда:

Постепенно увеличивая n, получаем следующие приближения для S_n.

	1.5	0.5
	1.833333	0.333333
	2.083333	0.25
	2.283333	0.2
	2.45	0.166667
	2.592857	0.142857

 

Как видите, на 7-й итерации величина S изменилась примерно на 0.14, что меньше заданного порога 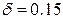. Таким образом, можно утверждать, что мы вычислили значение исходного ряда с заданной точностью.

Следует отметить, что на практике правильнее задавать требуемую точность δ не по абсолютному значению, а в виде относительной величины, например, δ = 1% от последнего приближения S, т.е. δ_n = Δ S_n / S_{n ,} где n – номер приближения. Критерий достижения требуемой точности и прекращения итераций: δ_n ≤ 1%.

Допустим, что теперь нам необходимо рассчитать сумму ряда:

 

 

с относительной погрешностью .

Воспользуемся полученным ранее результатом и оценим относительную погрешность вычисления суммы ряда на каждой итерации.

 

	1.5	0.5	0.33
	1.833333	0.333333	0.18
	2.083333	0.25	0.12
	2.283333	0.2	0.08
	2.45	0.166667	0.06
	2.592857	0.142857	0.05

 

Построим зависимость от (рис. 25).

 

Рис. 25

 

Обратите внимание на то, что погрешность вычисления резко уменьшается на начальных итерациях. В дальнейшем, с увеличением выигрыш в точности вычисления стремится к нулю. Именно поэтому на практике для достижения определенной точности расчетов задаются относительной погрешностью, а не абсолютным значением. Именно относительная погрешность позволяет достичь необходимой точности ограничив при этом число итераций, а следовательно и машинных ресурсов.

 

Решение типовых задач

 

Задача 1. Дана аналитическая функция . Найти значение определенного интеграла на интервале [a,b] с заданной точностью .

 

Решение.

Будем решать задачу методом правых прямоугольников.

Листинг 37

/*Определенный интеграл вычесленный с заданной точностью*/

#include <fstream.h>

#include <math.h>

void main(void)

{

// Границы интервала

double dA, dB;

cout << "Input interval [a,b]\n";

// Проверка правильности ввода интервала.

// В случае ошибки ввод повторяется

bool bKey = false;

while (!bKey)

{

cin >> dA >> dB;

if (dA < dB)

{

bKey = true;

}

else

{

cout << "Wrong interval [a,b]\n";

}

}

 

cout << "Input threshold\n";

double dThreshold;

// Ввод заданной точности

cin >> dThreshold;

 

// Количество частичных интервалов

int nCount = 10;

// Расчет шага аргумента

double dDeltaX = (dB - dA) / nCount;

// Прерыдущее и следующее приближение значения интеграла

double dResultPrev = 0, dResultNext;

// Расчет первого приближения интеграла

for (int i = 0; i < nCount; i++)

{

dResultPrev = dResultPrev + 2 * (dA + dDeltaX * i) * dDeltaX;

}

// Увеличения числа частичных интервалов

nCount = nCount * 2;

// Перерасчет шага аргумента

dDeltaX = (dB - dA) / nCount;

// Изначально принимаем погрешность вычисления первого приближения

// значения интеграла заведомо большей заданной

double dError = dThreshold + 1;

// Повторяем итерации до тех пор пока не достигнута заданная точность

while (dError > dThreshold)

{

// Вычисляем ичередное приближение

dResultNext = 0;

for (i = 0; i < nCount; i++)

{

dResultNext = dResultNext + 2 * (dA + dDeltaX * i) * dDeltaX;

}

// Определяем погрешность вычисления

dError = fabs(dResultNext - dResultPrev);

dResultPrev = dResultNext;

// Выводим промежуточный результат на экран

cout <<"Number of interval: "<<nCount<<"\t Error: "<<dError<<"\n";

// Увеличиваем число частичных интервалов

// и перасчитывем шаг аргумента

nCount = nCount * 2;

dDeltaX = (dB - dA) / nCount;

}

// Выводим на экран конечный результат

cout << "Result: " << dResultPrev << "\n";

}

 

Тестовый пример

На интервале [0, 2] значение интеграла от функции равно:

 

 

Проводим тестирование программы.

Вводим интервал интегрирования [0, 2], точность расчета — 0.1.

 

Протокол работы программы:

Input interval [a,b]

Input threshold

0.1

Number of interval: 20 Error: 0.54

Number of interval: 40 Error: 0.285

Number of interval: 80 Error: 0.14625

Number of interval: 160 Error: 0.0740625

Result: 3.92531

 

Повторяем расчет с повышенной точностью 0.01.

Протокол работы программы:

Input interval [a,b]

Input threshold

0.01

Number of interval: 20 Error: 0.54

Number of interval: 40 Error: 0.285

Number of interval: 80 Error: 0.14625

Number of interval: 160 Error: 0.0740625

Number of interval: 320 Error: 0.0372656

Number of interval: 640 Error: 0.0186914

Number of interval: 1280 Error: 0.00936035

Result: 3.99063

 

Задание на лабораторную работу №10

 

Задача 1. Дана аналитическая функция . Вид функции выбрать в соответствии с таблицей 8.1. Найти значение определенного интеграла на интервале [a,b] с заданной точностью .

 

Оформить протокол лабораторной работы.

 

Примечание! Алгоритмы решения задач должны содержать не только расчетную часть, но и блоки формирования входных и выходных данных, а также блоки проверки правильности вводимых данных.

 

Варианты заданий

 

Таблица 8.1. Варианты заданий

№	Функция	№	Функция	№	Функция

 

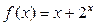
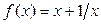
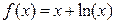
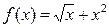
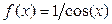
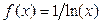
Контрольные вопросы

 

1. Вам необходимо расчитать некую величину с заданной точностью. Ваши действия?

 

Литература

 

1. Керниган Б., Ритчи Д. Язык программирования Си. \ Пер. с англ., 3-е изд., испр. – СПб.: “Невский диалект”, 2001. – 352 с.: ил.

2. Черносвитов А. Visual C++ и MFC. Курс MCSD для профессионалов – СПб: Издательство “Питер”, 2000. – 544 с.: ил.

3. Трой Д. Проектирование на языке Си для персонального компьютера IBM PC: Пер. с англ. – М.: Радио и связь, 1991. – 432 с.: ил.

4. Шилдт Г. Самоучитель С++: Пер. с англ. – 3-е изд. – СПб.: БХВ-Петербург, 2006. – 688 с.