Ранее мы отмечали, что спектр выходного колебания реального СЧ в установившемся после переключения режиме отличается от идеального гармонического колебания. Наличие дискретных и шумовых составляющих в тракте формирования этого колебания приводит к паразитным отклонениям от номинального значения амплитуды, фазы и частоты колебания.
Для количественной оценки этих отличий дадим математическое описание выходных колебаний СЧ.
2.1. Математическая модель выходного сигнала СЧ
Сигнал реального генератора СЧ запишем в виде
uр(t) = U(t) cos(ω0t+Ф(t)). (2.1)
где Ф(t) начальная фаза, зависящая от времени.
Амплитуда U(t) не вносит изменений в частоту колебаний. Исключение составляет случай, когда амплитудная модуляция (AM) переходит в фазовую (частотную) модуляцию в нелинейных усилителях и умножителях частоты.
Мгновенная (круговая) частота колебаний определяется производной от полной фазы
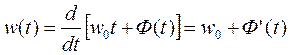(2.2)
где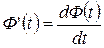 
. (2.3)
Среднее значение частоты реального генератора за бесконечный интервал времени Т равно
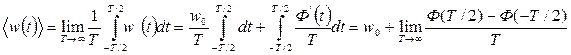(2.4)
За среднее значение частоты идеального генератора выбирают частоту ω0 генератора , у которого среднее значение начальной фазы Ф(t) равно нулю
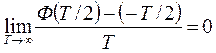(2.5)
В этом случае начальная фаза Ф(t) реального СЧ представляет собой мгновенное значение фазового сдвига его колебания по отношению к фазе идеального генератора частоты w0, a Ф'(t) - отклонение частоты реального от частоты wq идеального генератора.
Выходная частота СЧ с одним опорным генератором частоты f0 определяется соотношением: fвыx = N f0, где N - рациональное число. Нормированное отклонение любой выходной частоты синтезатора, удовлетворяющей условию когерентности, совпадает с относительным отклонением частоты ОГ:
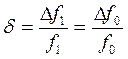(2.6)
Величина δ остается неизменной при операциях умножения и деления частоты и облегчает сравнение источников с разными значениями частот.
Кратковременная нестабильность фазы и частоты измеряются в течение конечного интервала времени в виде оценок:
Среднее значение отклонения частоты определяется средним на интервале времени τ значением
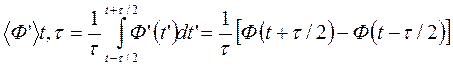, (2.7)
где <...>- означает усреднение на интервале времени τ.
Накопление фазы за время τ при отклонении частоты определяется как
. (2.8)
Среднее значение отклонения фазы на интервале времени τ
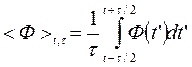. (2.9)
В этих выражениях процессы Ф(t), Ф'(t) и ‹Ф›t,τ и ‹Ф'›t,τ для установившегося режима СЧ полагаются случайными функциями.
Поэтому кратковременные нестабильности этих процессов выражаются через характеристики случайных функций х(t): дисперсию s2, корреляционные функции и спектральные плотности, в частности, дисперсию в виде
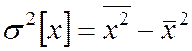, (2.10)
где черта означает временное на интервале Т >> τ или статистическое среднее.
В этом случае дисперсия среднего значения отклонения частоты (2.7) на интервале Т, согласно (2.10) равна:
, (2.11)
т.к. по определению (2.5) и (2.7)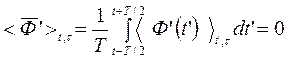 
и среднее значение отклонения частоты -центрированный процесс.
Покажем, что вредное влияние побочных дискретных и шумовых составляющих выходного сигнала СЧ может быть сформулировано в терминах паразитной АМ, ЧМ, ФМ модуляции.
Пусть модулирующее (побочное) колебание является синусоидальным с амплитудой Е m и частотой ωm =2pFm: Тогда:
1) для АМ модулированного колебания
e(t)=Ec[1+mcosωmt]cosωct (2.12)
где m=ka Em /Ec, ka - коэффициент пропорциональности, а
Ec - амплитуда несущей, имеем спектр рис.2.1:
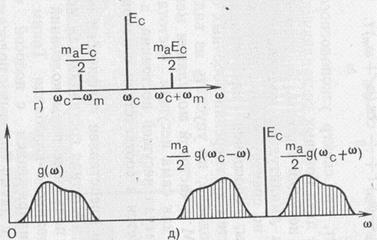рис.2.1.
Откуда отношение боковой (паразитной) к несущей спектральной составляющей 0,5 ma Ec /Ec =m/2 определяет индекс глубины АМ модуляции
Отметим, что, паразитная АМ может преобразоваться в паразитную ФМ в нелинейных элементах синтезатора, у которых фазовые характеристики (или время задержки) зависят от мгновенного значения амплитуды входного колебания.
2) для ЧМ модулированного колебания
e(t)=Eccos (ωct+βsin ωm t), (2.13)
где β= kf Em/ ωm =Δfпик /Fm - индекс модуляцииЧМ в радианах,
Δfпик -девиация частоты. При малых β<<π/2 имеем спектр рис.2.2:
e(t) ≈ Ес [ cosωct- β/2 соs(ωc- ωm)t + β/2 соs(ωc+ ωm)t]
Таким образом, ЧМ сигнал имеет спектр, который отличается от спектра АМ инверсией на π нижней боковой полосы.
Однако, отношение боковой к несущей спектральной составляющей,как и для АМ, равно индексу ЧМ 0,5 β Eс /Ес = β/2.
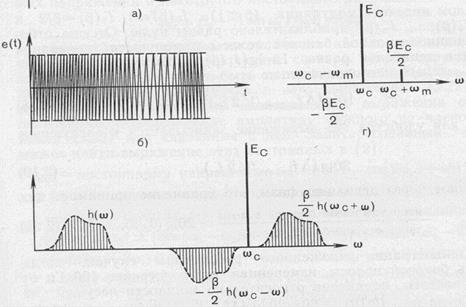рис.2.2.
3 ) для ФМ модулированного колебания
e(t)=Ecsin (ωct+θdsin ωm t), (2.14)
где θd=k Eт- максимальнаядевиация фазы в радианах.
Спектр ФМ аналогичен спектру ЧМ и θd= β = Δfпик /Fm
Выводы: Наличие и вредное влияние побочных колебаний проявляется в паразитной АМ, ЧМ, ФМ модуляциях. Его можно оценить отношением (в децибелах) мощности одной боковой полосы к мощности колебания несущей частоты сигнала.
В частности, для ЧМ(ФМ) это отношение равно 10 lg (β /2)2. т.е.:
10 lg (Δfпик /2Fm)2=10lg(Δfэф / √ 2Fm)2 =20lg(Δfэф / √ 2Fm),. (2.15)
или выраженное через девиацию фазы, равно:
20 lg (θd /2). (2.16)
При этом, наличие побочных составляющих в спектре выходного сигнала СЧ свидетельствует:
-при симметричном спектре -о наличие паразитной АМ;
-при несимметричном спектре - о наличие комбинации паразитных АМ, ЧМ (ФМ) модуляций, так как фазовые спектры АМ и ЧМ при отрицательных частотах противофазны и взаимно компенсируются.
Таким образом, при описании сигналов (2.1) СЧ представляют интерес следующие величины в спектральной области:
1.Полный или радиочастотный спектр сигнала, включающий несущую и все боковые полосы.
2.Спектральная плотность шума Sш(f): - определяется отношением мощности шумов на частоте F одной боковой полосы в полосе частот 1 Гц к мощности сигнала СЧ (размерность 1/Гц.).
Её можно оценить идеальным анализатором спектра с полосой пропускания 1Гц. При этом мощность шума включает в себя составляющие, вызванные как амплитудными, так и фазовыми флуктуациями сигнала. Спектральную плотность паразитной AM можно найти, детектируя сигнал идеальным амплитудным детектором и измеряя спектр на его выходе. Обычно паразитная AM устраняется пропусканием сигнала через ограничитель, поэтому ее можно не учитывать. Под Sш(f) будем понимать далее шумы, вызывающие фазовую (частотную) модуляцию.
З.Спектральная плотность фазовых флуктуаций Sφ(F) определяется как средний квадрат sj2 (2.10) отклонения фазы сигнала от ее номинального значения под действием шумов на частоте F в полосе 1 Гц. Ее можно наблюдать, анализируя спектр сигнала, прошедшего через идеальный фазовый детектор (ФД). Так как Sφ(F) вызывается действием шумов обеих шумовых полос, то
Sφ(F)=2S ш (F) [рад2/Гц] (2.17)
4.Спектральная плотность частотных флуктуаций Sf(F), определяется как средний квадрат sf2 (2.11) отклонения частоты сигнала от ее номинального значения под действием шумов на частоте F в полосе 1 Гц. Измеряется наблюдением спектра сигнала, прошедшего через идеальный частотный детектор (ЧД).
Sf(F) = F 2 Sφ(F) = 2 F 2S ш (F) [Гц2/Гц](2.18)
5.Спектральная плотность относительного отклонения частоты Sy(F) определяется относительно несущей fc = f0 как
Sν(F) = (F/f0)2 Sφ(F). [ Гц -1 ] (2.19)
Величина Sν(F), имеющая размерность 1/ Гц, является удобным показателем стабильности частоты в частотной области преобразований Фурье. Она позволяет наглядно сравнивать синтезаторы с различными номинальными частотами при построении на одном графике соответствующих зависимостей.
2 .2. Оценка спектральных плотностей
Оценка (измерение) спектральных плотностей обеспечивает однозначную идентификацию видов шумовых процессов в реальных генераторах и позволяет оценить уровни ПОА, ПОЧ и ПОФ.
При описании спектральных плотностей наиболее употребительна на практике модель, основанная на описании S(F) степенными функциями:
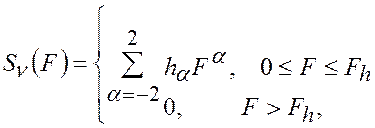(2.20)
где ha - постоянная меры измерения уровня шума, а значение a характеризует вид шума;
Fh - верхняя граничная частота резкого спада S(F).
Нижняя граничная частота обычно не вводится, но на практике она составляет 10-20Гц (для анализаторов и измерителей малых паразитных девиаций). В радиосвязи, например, при передаче информации в аналоговой форме она определяется нижней граничной частотой телефонного канала 300 Гц (верхняя - 3400 Гц). При передаче информации в цифровой форме FH = 0,01 R, FB= R, где R - электрическая скорость передачи информации
Измерительные данные обычно отображают на графике в двойном логарифмическом масштабе. Поэтому степенные функции модели (2.20) представляют собой прямые линии, по наклону которых можно установить значение a, т.е. вид шумов. Типичный график спектральной плотности мощности фазовых шумов представлен на рис. 2.3.
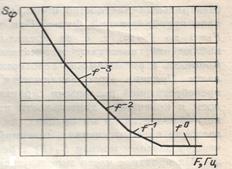Рис. 2.3.
В табл. 2.1 даны выражения спектральных плотностей Sy(F) и Sφ(F) для видов шумов согласно модели (2.20), где из формулы (2.19)
Sφ(F) = fo2 Sν(F) / F2
Таблица 2.1
| Sν(F) | Sφ(F) | Название шума |
| h-2F-2 | fo2 h-2 F-4 | Частотный шум случайных блужданий |
| h-1F-1 | fo2 h-1 F-3 | Частотный фликкер - шум |
| h0 | fo2 h0 F-2 | Белый частотный шум |
| h1F | fo2 h1 F-1 | Фазовый фликкер - шум |
| h2F2 | fo2 h2 F0 | Белый фазовый шум |
Рассмотрим физические источники этих шумов.
В электронных компонентах всегда есть источники белого и фликкер - шумов. В зависимости oт расположения этих источников в генераторах имеет место:
- паразитная ФМ модуляция входными шумовыми процессами при внешних источниках шума;
- паразитная ЧМ при внутренних источниках шума.
Кроме того, имеют место следующие мультипликативные шумы, которые непосредственно модулируют частоту или фазу.
1. Частотные шумы:
-Частотный шум случайных блужданий( F-2 в Sν(F)) обычно связан с воздействием на генератор окружающей среды (t0, вибрации, удары и т.д.).
-Частотный фликкер-шум (F-1 ). Происхождение пока недостаточно изучено. Предполагается, что он связан с контактной и поверхностной неоднородностью в полупроводниках. Его источником служат флуктуации проводимости среды, через которую протекает ток.
-Белый частотный шум (F0 ) вызывается источниками аддитивного белого шума, действующими внутри контура обратной связи генератора (например, теплового шума).
2. Фазовые шумы:
- Фазовый фликкер-шум (F-1 в Sφ(F)) обычно обусловлен шумящими электронными yзлами, например выходными усилителями или умножителями частоты, и может быть уменьшен отрицательной ОС по высокой частоте и выбором малошумящих элементов.
-Белый фазовый шум (F0 в Sφ(F)) вызывается источниками аддитивного белого шума, внешними по отношению к цепи ОС генератора, например, БУ. Для его уменьшения полезна полосовая фильтрация сигнала на выходе генератора.
Оценим по измеряемым данным уровни ПОА, ПОЧ и ПОФ, введенные согласно ОСТ 4.208.012-77,1979 «Аппаратура синтеза частот для радиосвязи. Термины и определения».
Уровень ПОА - это отношение среднего квадратичного значения суммы спектральных составляющих паразитного отклонения амплитуды колебания, лежащих в заданной полосе частот, к среднему квадратичному значению выходного колебания СЧ, выраженное в децибелах.
DПОA(FH,FВ)=20lg[Ua(FH,FВ)/U], (2.21)
где U -среднее квадратичное значение Up(t) -колебания(2.1) СЧ;
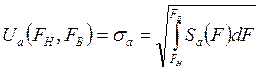.; (2.22)
спектральная плотность среднего квадрата ΔUа(t)
(2.23)
Уровень ПОЧ - это среднее квадратичное значение суммы спектральных составляющих паразитного отклонения частоты колебания (в герцах), лежащих в заданной полосе частот
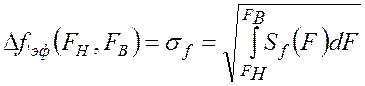, (2.24)
где спектральная плотность среднего квадрата отклонения Δf(t)
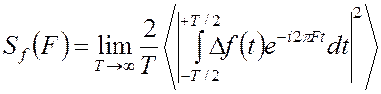(2.25)
Уровень ПОФ определяется (в градусах) как
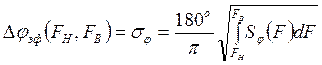, (2.26)
где спектральная плотность среднего квадрата отклонения Δφ(t)
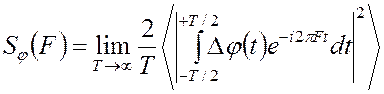, (2.27)
которая измеряется в радианах.
При оценке спектральных характеристик СЧ и генераторов различного типа, т.е. с разными частотами, удобно пользоваться выражением
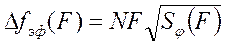(2.28)
где N коэффициент умножения частоты.
При оценивании шумовых свойств СЧ используют часто оценки максимального паразитного отклонения фазы или частоты.
Например, максимальные значения ПОЧ и ПОФ, при паразитной модуляции сигнала СЧ синусоидальным сигналом (дискретная составляющая спектра паразитной девиации частоты), равны:
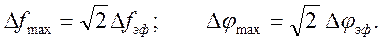(2.29)
Вместе с тем, максимальные значения ПОЧ и ПОФ при паразитной модуляции шумовым сигналом с гауссовским распределением ПОЧ и ПОФ равны:
Δfтax =2,58 Δfэф; Δφтах =2,58 Δ φэф. (2.29')
Однако, при наличии в спектре последнего кроме шумовых и дискретных составляющих, то это соотношение зависит от уровня дискретных и шумовых составляющих и с ростом дискретных смещается к значению Δfтax = 
.
Таким образом, по соотношению между среднеквадратической и пиковой девиациями можно судить о наличии дискретных побочных составляющих в спектре шумового сигнала.
