А. Сравнимые и несравнимые понятия.
Два понятия P и S являются сравнимыми, если они имеют хотя бы один общий для них родовой признак. Если такого признака нет, они не относятся к сравнимым понятиям (являются несравнимыми). Например, понятия «студент» и «курсант» являются сравнимыми, поскольку имеют общий родовой признак – «обучаться в вузе или среднем специальном учебном заведении», а понятия «факультет» и «университет» - несравнимы, поскольку у них такого признака нет. Отметим в этой связи, что следует различать два типа отношений: а) отношения понятий по объему, как это имеет место у понятий «судья» и «юрист»; б) отношения понятий, в одном из которых мыслится предмет как целое («университет»), а в другом – часть этого же предмета («факультет»). Различие этих отношений хорошо видно на наших примерах: про судью справедливо будет утверждать, что он – юрист, а про факультет нельзя сказать, что он есть университет.
Б. Совместимые и несовместимые понятия
Все сравнимые понятия подразделяются на совместимые и несовместимые. Понятия S и P совместимы, если их объемы имеют некоторые общие элементы. Если таких элементов нет, то эти понятия являются несовместимыми (хотя и сравнимыми!). Так, понятия «шахматист» и «студент» совместимы (некоторые студенты являются шахматистами, а некоторые шахматисты обучаются в вузе). Понятия же «защитник» и «судья» - несовместимы (ни один юрист не может одновременно, в рамках одного и того же судебного процесса, быть и защитником подсудимого, и судьей).
Виды совместимости понятий. Выделяют три типа совместимости понятий:
1) Равнозначность. Понятия S и P находятся в отношении равнозначности, если каждый элемент объема понятия S входит в объем понятия P, а каждый элемент объема понятия P входит в объем понятия S. Примеры: «административный центр России»(S) и «политический центр России»(P); «равноугольный треугольник»(S) и «равносторонний треугольник» (P). Для равнозначных понятий существенно, чтобы их содержания имели какие-то различия по составу признаков (иначе не будет двух понятий, а одно, но выраженное разными словами).
Отношения равнозначных понятий по объему можно представить графически с помощью круговых схем:

В этой схеме равнозначность понятий S и P выражена тем, что их объем представлен площадью одного и того же круга.
2) Подчинение. Понятие S подчиняет понятие P (S является подчиняющим, а P- подчиненным), если каждый элемент объема понятия P входит в объем понятия S, но не каждый элемент объема понятия S входит в объем понятия P. Это означает, что понятие S является родовым по отношению к P, а понятие P – видовым по отношению к S. Примеры: «треугольник» (S) и «прямоугольный треугольник» (P). Схематически:

3) Перекрещивание. Понятия S и P находятся в отношении перекрещивания, если выполняются следующие условия:
- Некоторые элементы (по меньшей мере, один) объема понятия S не входят в объем понятия P;
- Некоторые элементы объема понятия P не входят в объем понятия S;
- Некоторые элементы понятия S входят в объем понятия P, и наоборот.
Примеры: «студент» (S) и «спортсмен» (P); «роман» (S) и «поэма» (P). Схематически:

Виды несовместимости понятий. Их также три:
1) Противоречие. Понятия S и P находятся в отношении противоречия, если выполняются следующие условия:
a. Никакой элемент объема понятия S не входит в объем понятия P;
b. Никакой элемент понятия P не входит в объем понятия S;
c. Объемы понятий S и P исчерпывают объем родового по отношению к ним понятия Q.
Примеры: «трезвый человек» (S) и «нетрезвый человек»(P), «инфекционное заболевание»(S) и «неинфекционное заболевание» (P). Схематически:
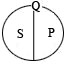
2) Противоположность. Понятия S и P находятся в отношении противоположности, если выполняются следующие условия:
a. Никакой элемент объемапонятия S не входит в объем понятия P
b. Никакой элемент понятия P не входит в объем понятия S;
c. Видовые отличия понятий S и P таковы, что они характеризуют крайние степени какого-либо признака родового понятия Q.
Примеры: «студент-отличник»(S) и «студент-двоечник»(P), «старик»(S) и «ребенок»(P). Схематически:
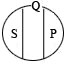
Противоположность понятий S и P на схеме представлена тем, что их объемы расположены на разных «полюсах» круга, символизирующего объем родового понятия.
3) Соподчинение. Понятия S и P находятся в отношении соподчинения, если они не являются ни противоречащими, ни противоположными, находясь в то же время в подчинении у одного и того же родового понятия Q.
Примеры: «дерево»(S) и «трава»(P) подчиняются понятию «растение». Схематически:

*Для правильного решения вопросов об отношении понятий иногда полезно уточнить их содержание по словарю (или энциклопедии) той области знаний, из которых взяты данные понятия.






