Введение
Прежде чем приступить к выполнению лабораторных работ по геометрической оптике студентам следует познакомиться с основными понятиями и формулами теории геометрической оптики, краткое изложение которых приведено ниже в §§1-7.
§1. Исходные понятия геометрической оптики
В данном практикуме изучаются центрированные оптические системы со сферическими границами (поверхностями) прозрачных оптических сред, отличающихся показателями преломления. Плоская граница является частным случаем сферической границы (r ® ¥). Следует заметить, что в оптическом эксперименте иногда будут использоваться и другие виды линз. Так, например, в лабораторном практикуме по волновой оптике при постановке дифракционного эксперимента, наряду со сферическими линзами, будут использоваться цилиндрические линзы. В отличии от сферических линз цилиндрические линзы собирают свет только в одном направлении. Благодаря этому их свойству цилиндрические линзы позволяют преобразовать точечное изображение в линию, удобны для фокусировки света от щели, а также для изменения высоты изображения без изменения его ширины. В качестве конденсора кодоскопа в лаборатории используется линза Френеля, состоящая из отдельных примыкающих друг к другу концентрических колец небольшой толщины, которые в сечении имеют форму призм определенного профиля. Из-за малой толщины линзы Френеля имеют хороший коэффициент пропускания.
При построении изображений в оптической системе в геометрической оптике используются лучевые представления. Луч -линия, вдоль которой происходит перенос световой энергии. Источник света, размерами которого можно пренебречь по сравнению с расстояниями, на которых изучается действие света, называется точечным источником. Точечный источник света в однородной среде порождает пучок радиально расходящихся лучей. Световой пучок, исходящий из точечного источника, называется гомоцентрическим пучком. Гомоцентрическому пучку в однородной изотропной среде соответствует сферическая волновая поверхность (сферическая волна). Пучок параллельных лучей (плоскую волну) можно рассматривать как предельный случай гомоцентрического пучка с источником, удаленным на бесконечность. В изотропной среде волновая поверхность нормальна к лучам пучка.
В неограниченной однородной среде волновые и лучевые представления о распространении света приемлемы в одинаковой мере. При наличии же неоднородностей, преград или диафрагм сказывается явление дифракции, объясняемое только с волновой точки зрения.
|
, (1.1)
где ФR, ФT и Ф - усредненные по времени потоки лучистой энергии отраженного, преломленного и падающего световых пучков. Для оптически прозрачных сред
|
Электромагнитная теория света при малых углах падения, - i £ 15°, дает следующие выражения для коэффициентов R и T:
(1.3)
Из этих формул следует, что при небольших углах падения от поверхности стекол (n’= 1.6) отражается незначительная часть света (R ~ 0,04).
Направление отраженных и преломленных лучей описывается законами отражения и преломления света:
1. Лучи падающий, отраженный и преломленный лежат в одной плоскости с нормалью, проведенной к границе двух сред через точку падения. Эта плоскость называется плоскостью падения луча.
2. Синус угла падения (- i) равен синусу угла отражения (i):
(1.4)
3. Отношение синуса угла падения к синусу угла преломления для данных двух сред есть величина постоянная, не зависящая от величины угла падения и равная 
:
(1.5)
Законы отражения и преломления света лежат в основе геометрической оптики. Они могут быть выведены из волновой теории света, основанной на обобщенных законах электромагнетизма.
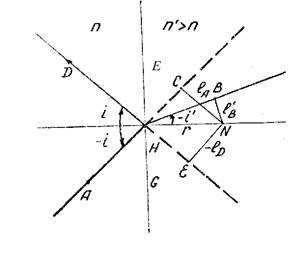
Оптической осью для плоской границы двух сред (рис. I) является нормаль НN к границе EG. Горизонтальные отрезки на оптической оси отсчитываются от выбранных "кардинальных" точек, например, от точки Н. Принято следующее правило знаков для отрезков и углов. Отрезки, отсчитываемые по ходу светового луча, положительные, отсчитываемые против хода светового луча - отрицательные. Положительное направление оптической оси совпадает с направлением луча. Вертикальные отрезки, лежащие выше оптической оси, - положительные, ниже – отрицательные. Углы отсчитывают от оптической оси до луча (или его продолжения) по кратчайшему угловому пути. Если отсчет производится по часовой стрелке - углы положительные, против часовой стрелки - отрицательные. На рисунках отрицательные отрезки и углы отмечают знаком минус, т.е. на рисунках приводятся положительные значения этих величин. Пространство, где расположены объекты, называется пространством объектов, а где расположены изображения - пространством изображений. На рисунках буквенные обозначения отрезков и углов, расположенных в пространстве изображений, обычно отмечают штрихом.
Как видно из рис.1,
, (1.6)
где отрезок r отсчитывается от точки H до произвольной (в случае плоской границы) точки N, лежащей на оптической оси; lA,,-lD и l’B – длины отрезков, лежащихна перпендикулярах, опущенных из точки N на направление или продолжение лучей.
После подстановки (1.6) в законы отражения и преломления (1.4 и 1.5) получим:
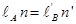(1.7)
(1.8)
Отсюда можно записать равенство:
(1.9)
Равенство (1.9) утверждает, что оптическая длина "плеча" любого светового луча при преломлении и отражении для данных двух прозрачных сред является оптическим инвариантом данного луча.
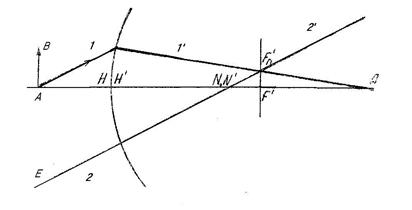
Преломление света на сферической границе раздела двух прозрачных сред.
На рис.2 изображено отражение и преломление светового луча АВ в точке В,лежащей на сферической границе. Оптической осью сферической границы является прямая АА’, проходящая через центр кривизны N и вершину Н сферической границы. Ниже при рассмотрении свойств оптических систем будет показано, что в центре кривизны в случае одной сферической границы располагаются обе узловые точки системы N и N'. В вершине Н сферической границы располагаютсяглавные точки Н и Н’. В общем случае кардинальные точки H и H’, N и N’ не совпадают друг с другом. Определения главных и узловых точек будут даны ниже. Точка A - действительная точка предмета, лежащая на оптической оси, A’ – ее действительное изображение, образованное преломленными лучами, А” – мнимое изображение точки А, образованное отраженными
 |
лучами. Мы
|
ограничимся рассмотрением изображения, образованного только преломленными лучами. Все формулы, для преломляющей сферической границы, справедливы и для отражающей сферической границы, если только учесть, что при отражении – n’= n. Также заметим, что все определения, характеристики и формулы, относящиеся к сферической границе, записанные в общем виде, полностью применимы к любой сложной центрированной оптической системе. Будем считать, что рассматриваемая оптическая система (сферическая граница) является идеальной в том смысле, что она позволяет получить неискаженные оптические изображения предметов. В идеальной оптической системе каждой точке предмета А соответствует в пространстве изображений одна точка А’, являющаяся стигматическим изображением точки А. "Стигма” - означает точка. Две точки, линии или поверхности, одна из которых является изображением другой, называются сопряженными. А и А’ - сопряженные точки. Идеальное (стигматическое) изображение можно получить только при использовании лучей, идущих вблизи оптической оси. Лучи, идущие вблизи оптической оси, называются параксиальными лучами. На практике параксиальные лучи не используют, поскольку они соответствуют бесконечно малым углам и, u’ и бесконечно малым вертикальным отрезкам h. Для приближенного нахождения хода световых лучей через оптическую систему используют так называемые "нулевые" лучи с достаточно большими для практики углами и и вертикальными отрезками h. При этом нулевым лучам условно приписывают те же свойства, что и параксиальным лучам. Такую воображаемую систему называют идеальной.
Как видно из рис. 2, в рассматриваемом примере сферическая граница преобразует расходящийся гомоцентрический пучок с центром в точке А в сходящийся гомоцентрический пучок с центром в точке А ‘. Выражение для оптического инварианта преломления в данном случае можно записать
в виде:
или 
(2.1)
В приближении параксиальных лучей, которое называется Гауссовым приближением,
(2.2)
Подставив (2.2) в (2.1), имеем:
, 
Поделив все члены последнего равенства на произведение aa’r, получимформулу для сферической границы раздела двух сред:
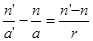, (2.3)
здесь отрезки a и a’ определяют положение предмета и его изображенияи отсчитываются от передней и задней главных точек H и H’, которые в случае одной сферической границы совпадают, r – радиус кривизны сферической границы. Правая часть формулы (2.3) называется оптической силой сферической границы, обычно обозначается буквой Ф:
(2.4)
Оптическая сила Ф является однозначной характеристикой сферической границы двух оптических сред, не зависит от направления света. Для параксиальных лучей также не зависит от расстояний a и a’, т.е. в этом случае при заданном a положение изображения определяется однозначно (a' = сопst) и образуется стигматическое изображение, преломленный пучок сохраняет свой гомоцентризм. Для непараксиальных лучей оптическая сила оказывается зависящей от углов (-i, i’, -u, u’), что приводит к нарушению гомоцентризма световых пучков и, следовательно, к искажению изображений, в частности, к сферической аберрации. Оптическая сила - положительная, если лучи, исходящие из действительной точки предмета, находящейся на оптической оси, при преломлении отклоняются в сторону оптической оси. Таким образом, оптическая система с положительной оптической силой является собирающей. Рассеивающая оптическая система обладает отрицательной оптической силой. Если правую часть формулы (2.3) обозначить как оптическую силу и переписать ее в виде (2.3а):
(2.3а),
то в такой записи эта формула справедлива для любой центрированной оптической системы, где Ф - оптическая сила соответствующей оптической системы. Оптическая сила в системе СИ измеряется в диоптриях.
§3. Фокусы, фокусные расстояния и фокальные плоскости оптической системы
Практическая полезность формулы (2.3а) для параксиальных лучей состоит, в частности, в том, что она позволяет вычислить положение изображения А’ при известном положении предмета А и, наоборот. При этом важным является случай, когда a = -¥, т. е. точка А действительного предмета находится достаточно далеко от сферической границы. В этом случае точка, сопряженная с точкой А обозначается F’ и называется задним фокусом оптической системы, отрезок а' = Н'Р’ обозначается f’ и называется задним фокусным расстоянием оптической системы (рис. 3а). Вертикальная плоскость (нормальная к оптической оси), содержащая точку F', называется задней фокальной плоскостью. Таким образом, точка F’ сопряжена с точкой А бесконечно удаленного действительного предмета, лежащей на оптической оси. Соответственно, задняя фокальная плоскость сопряжена с бесконечно удаленной действительной плоскостью. Из формулы (2.3а) получим, что при a = - ¥
(3.1)
 |
В случае одной преломляющей сферической границы с учетом формулы (2.4) имеем:
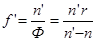(3.1а)
Рис.3а
Аналогично (рис.36), полагая a‘ = ¥, введемпонятия переднего фокуса F, переднего фокусного расстояния f и передней фокальной плоскости:
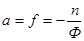(3.2)
В случае одной преломляющей сферической поверхности
(3.2а)
Nbsp; Рис.3б
Таким образом, передний фокус F сопряжен с точкой А’, находящейся на оптической оси в пространстве изображений и бесконечно удаленной от точки Н’. Как следует из (3.1) и (3.2) абсолютные величины фокусных расстояний ÷ f ÷ и ÷ f’ ÷, вообще говоря, не равны друг другу:
(3.3)
Лишь в частном случае, когда оптическая система находите в однородной среде (n’=n), ÷ f ÷ = ÷ f’ ÷. Это имеет место, например, для лупы, окуляра микроскопа, телескопа и других оптических систем, находящихся в воздухе. Формулы (3.1 – 3.3) верны для любой оптической системы. Формулы (3.1а) и (3.2а) справедливы только для одной преломляющей сферической границы. Заметим, что в последнем случае если r>о и n’>n,то f’ > r всегда, в то время как f может быть и больше и меньше r. Введение фокусных расстояний f и f’ позволяет несколько иначе записать формулу (2.3). Если разделить все члены формулы (2.3а) на Ф, то с учетом (3.1) и (3.2) получим:
(3.4)
В случае оптической системы, находящейся в однородной среде, f = - f’ и
(3.5)
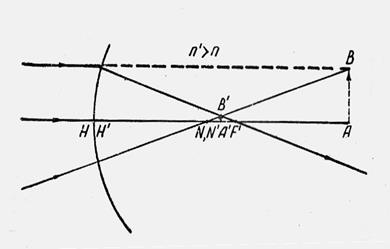
Для экспериментального определения фокусного расстояния оптической системы (толстой линзы, объектива и т.п.) удобно использовать формулу Ньютона (3.7), в которой положение предмета АВ и его изображения A’B’ (рис. 4) определяются отрезками – x и x’, отсчитываемыми от фокусов F и F’. Из рис.4 имеем:
(3.6) или
x x’ = f f’ (3.7)
При n’ = n (например, линза в воздухе)
x x’ = - f 2 = -f’ 2 (3.7а)
|
 |
|
§4. Увеличение оптической системы
 |
На рис. 5а показан прием построения изображения А’ действительной точки А, находящейся на оптической оси. На рис.5б, показаны 4 приема построения изображения В’ действительной точки В, не лежащей на оптической оси. На рис. 5в и 5г показаны аналогичные приемы построения
| ||||
| ||||
|
 |
|
 |
|
 |
|
изображения точек мнимого предмета АВ.
Отношение поперечных размеров изображения к сопряженным с ними размерам предмета называется линейным поперечным увеличением b:
, (4.1)
где y’ = A’B’, y = AB. Из рис.5б имеем:
откуда 
Выражая r через а и a‘ из формулы для сферической границы (2.3), окончательно получим, что 
(4.2)
Из соотношения (З.6) также имеем, что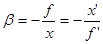 
(4.2а).
Несложно показать, что рассеивающая линза в воздухе всегда дает только мнимое (a’<0), прямое (b>0), уменьшенное (
) изображение действительного (а<0) предмета. Собирающая линза дает прямое и уменьшенное изображение только для мнимого (a>0) предмета, при этом само изображение оказывается действительным (рис. 5г). Поперечное увеличение изображения действительного предмета, даваемое собирающей линзой, может принимать любые значения: положительные, отрицательные, больше и меньше единицы в зависимости от расположения предмета относительно линзы. В случае мнимого изображения показатель преломления пространства изображения относится к той среде, через которую проходят действительные преломленные лучи.
Две сопряженные плоскости, для которых b =1, называются главными плоскостями. Из сказанного выше следует, что равенство b =+1 возможно, если предмет мнимый (a > 0, a’ > 0 ) или изображение мнимое (a < 0, a’ < 0), причем абсолютные величины a и a’ стремятся к нулю. Следовательно, для сферической преломляющей границы главные плоскости совпадают и касательны к поверхности границы в точке Н (H’). Главные плоскости всегда перпендикулярны оптической оси и в общем случае не совпадают друг с другом. Точка пересечения H передней главной плоскости с оптической осью называется передней главной точкой, а сопряженная с ней точка Н’, лежащая на пересечении задней главной плоскости с оптической осью, называется задней главной точкой.
На рис.6 показан предмет в виде треугольника АВС и его изображение А’В’С’. Направим луч АД вдоль гипотенузы АС. Отношение
(4.3)
 |
называется угловым увеличением.
|
Из рис.6 в параксиальном приближении имеем:
(4.4)
Сравнивая выражения (4.2) и (4.4), получим, что
(4.5)
В частном случае, для оптической системы в однородной среде (n’ = n) 
.
Например, телескоп дает уменьшенное изображение Луны (½b½<< 1) при очень большом угловом увеличении (g >> 1). Последнее условие необходимо для разрешения близких друг к другу деталей изображения предмета, находящегося на большом расстоянии.
Сопряженные точки, для которых g=1, называются узловыми точками, а плоскости, проходящие через узловые точки и нормальные к оптической оси, называются узловыми плоскостями. Для лучей, проходящих через узловые точки, u = u’, т.е. такие лучи после преломления в системе не изменяют своего первоначального направления. У сферической преломляющей границы обе узловые точки сливаются в одну и совпадают с центром кривизны поверхности N.
Фокусы, главные и узловые точки являются кардинальными точками оптической системы. У оптической системы, находящейся в однородной среде (n = n’) узловые и главные точки совпадают друг с другом (g = b =1).
Продольным увеличением a называется отношение продольных размеров изображения к сопряженным с ними продольным размерам предмета:
(4.6)
Из рис.6 имеем, что
, 
(4.7)
Сравнивая (4.5) и (4.7), получим, что
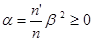(4.8)
Таким образом, продольное увеличение всегда положительное. Отсюда следует важный практический вывод: при перемещении предмета вдоль оптической оси его изображение смещается в ту же сторону. Из рис.6 также видно, что треугольники АВС и A’B’C’ никогда не бывают подобными, т.е. с помощью рассматриваемых оптических систем нельзя получит неискаженное пространственное изображение. В параксиальных лучах можно получить практически неискаженное изображение предмета, расположенного в вертикальной плоскости.
Наряду с рассмотренными выше коэффициентами увеличения b, a и g для оптических систем, включающих и глаз наблюдателя, вводится понятие видимого увеличения Г. Видимым увеличением называют отношение тангенса угла, под которым глаз наблюдателя видит изображение, образованное оптической системой и расположенное на расстоянии наилучшего зрения L0 от передней главной плоскости глаза, к тангенсу угла, под которым наблюдатель видит предмет невооруженным глазом (рис.7):
 |
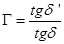(4.9)
Рис.7
Обычно линейным увеличением характеризуют масштаб изображения проекционных объективов. Масштаб изображения зрительных труб (телескопических систем) и микроскопов характеризуют видимым увеличением.
Работа № 1
Тонкие собирающие линзы
I. Цель работы
Научиться получать изображения с помощью линз. Познакомиться с различными методами измерения фокусных расстояний собирающих линз и уметь выполнять такие измерения.
П. Вопросы, знание которых необходимо для выполнения работы.
(Студент должен иметь по этим вопросам краткий конспект, с поясняющими чертежами)
1. Точечный источник света, световой луч.
2. Гомоцентрический пучок света.
3. Параксиальные лучи, Гауссова оптика.
4. Преломление света на сферической границе раздела двух сред. Оптическая сила и фокусные расстояния сферической преломляющей границы.
5. Увеличение: линейное, угловое, видимое.
6. Кардинальные точки и плоскости сферической границы раздела двух сред.
