Цель работы: Изучение устройства линзы Френеля и методики ее расчета.
Необходимые теоретические сведения
Линзы Френеля – это оптические элементы, имеющие ступенчатую поверхность. Они широко используются в датчиках, где не требуется высокого качества фокусировки: в световых конденсорах, увеличителях и устройствах фокусировки детекторов присутствия. Линзы Френеля изготавливаются из стекла, акрила (для видимого и ближнего ИК диапазона) и полиэтилена (для дальнего ИК диапазона). История линз Френеля началась в 1748 году, когда граф Буффо предложил вытачивать внутри стеклянных линз концентрические круглые ступеньки. Это позволило уменьшить толщину линз и снизить потери энергии. Однако в таких линзах преломление света происходит только на поверхности, поскольку внутри них лучи проходят строго по прямым линиям. Идея графа Буффо была модифицирована в 1822 году Августином Френелем (1788-1827), сконструировавшим линзы, кривизна различных колец которых зависит от расстояния до центра, в связи с чем, в таких устройствах практически отсутствует сферическая аберрация (сферическая аберрация — недостаток оптического изображения, заключающийся в том, что световые лучи, прошедшие вблизи оптической оси и лучи, прошедшие через отдалённые от оси части оптической системы (например, линзы), не собираются в одну точку).
На рис. 1 проиллюстрирована концепция линз Френеля на примере плосковыпуклых линз, разрезанных на несколько концентрических колец. После разрезки все кольца остаются линзами, направляющими падающие лучи в точку общего фокуса, положение которого определяется уравнением (для тонкой линзы, радиус кривизны которой намного больше толщины линзы):
 ,
,
где f – фокусное расстояние; r 1 и r 2 – радиусы кривизны линзы.
При изменении кривизны поверхности меняется угол преломления лучей. Части колец, показанные на рисунке буквами «х», не вносят никакого вклада в фокусирование лучей. При удалении этих секций (рис. 1,б) фокусирующие свойства линзы останутся прежними. Если теперь оставшиеся кольца сместить относительно друг друга до образования плоской поверхности (рис. 1,в), получится линза Френеля, фокусирующие свойства которой будут почти такие же, как у исходной плосковыпуклой линзы. Все концентрические элементы линз Френеля направляют падающие световые лучи в общую точку фокуса.
 а)
а)
  б) в)
б) в)
|
| Рис. 1. Концепция линз Френеля |
Линзы Френеля обладают рядом достоинств по сравнению с обычными линзами: небольшим весом, малой толщиной, способностью менять кривизну (справедливо для пластиковых линз), и, самое главное, низкими потерями на поглощение светового потока Последнее свойство особенно важно при изготовлении линз для среднего и дальнего ИК диапазонов, где поглощение в материалах может быть очень значительным. По этой причине почти все детекторы движения, работающие в дальнем ИК диапазоне, построены на основе линз Френеля.
В настоящее время широко применяются линзы Френеля двух типов: с постоянным шагом (рис. 2,а) и с постоянной глубиной (рис. 2,б). На практике бывает очень трудно изготовить линзы с одинаковой крутизной поверхности каждой ступени, поэтому все ступеньки выполняют с плоским профилем. Чтобы не ухудшать фокусирующие свойства линзы, все ступени должны располагаться, как можно, ближе друг к другу.
  а) б)
а) б)
|
| Рис. 2. Линзы Френеля: а) с постоянным шагом, б) с постоянной глубиной |
В линзах с постоянным шагом угол наклона φ каждого зубца зависит от расстояния h до оптической оси, поэтому по мере удаления от центра глубина зубцов возрастает. Если диаметр линзы, по крайней мере, в 20 раз меньше фокусного расстояния, ее центральная часть может быть плоской. Для более коротких фокусных расстояний центральная часть должна быть сферической. Угол наклона каждой ступени может быть определен по следующей формуле, справедливой только для малых значений h:

где f - фокусное расстояние; n – коэффициент преломления материала линзы.
В линзах с постоянной глубиной при увеличении расстояния от центра меняются и угол наклона φ, и расстояние между зубцами r. При расчете линз могут потребоваться следующие уравнения. Расстояние от зубца до центра может быть найдено по его порядковому номеру ξ (считается, что центр имеет нулевой порядковый номер):

а угол наклона зубца по формуле:

Полное количество ступеней в линзе может быть найдено через апертуру (максимальный размер) линзы D:

Линзы Френеля могут быть слегка изогнутыми, если этого требует конструкция датчика. Однако это может привести к смещению точки фокуса. Если линза изгибается внутрь радиуса кривизны, фокусное расстояние уменьшается.
Поскольку линзы со сферической поверхностью страдают от явлений аберрации, в устройствах, где требуется осуществлять фокусировку с высокой точностью, непрерывная поверхность линзы, контур которой определяется концентрическими зубцами, не должна быть сферической. На практике часто используется коническая поверхность с осевой симметрией относительно оси z, описываемая стандартным уравнением (рис. 3):
 ,
,
где Z и Y — координаты поверхности, С — вершина кривизны, а К— коническая константа. Вершина кривизны и коническая константа определяются требуемыми характеристиками линз, а контур каждого зубца задается уравнением:
 .
.
С и К определяются несколькими факторами: необходимым фокусным расстоянием, коэффициентом преломления и особенностями конструкции устройства, для которого пред- назначена линза.

|
| Рис. 3. Сравнение профилей сферической и конической линз |
Практическая часть
Основной задачей оптического расчёта френелевской линзы является нахождение формы второй (наружной) преломляющей поверхности каждого элемента, удовлетворяющей условию отклонения элементом фокальных лучей, падающих на соединительные грани (точки М и М0) параллельно оптической оси OZ (рисунок 4). Такому условию с определенной погрешностью удовлетворяет тороидная поверхность (безаберрационная поверхность должна быть поверхностью с переменным радиусом кривизны). Следовательно, оптический расчёт предполагает нахождение центра и радиуса кривизны второй преломляющей грани, а также координат узловых точек профиля элемента.

Рисунок 4 – Оптический расчёт элементов френелевской линзы с прямым внутренним несущим слоем
Расчёт линзы Френеля следует начинать с центрального элемента. Для уменьшения угловой величины и облегчения изготовления центральный элемент должен иметь толщину примерно равную или меньшую величины ti = t з заданной для всей линзы (рисунок 4)
Угол охвата 2φ0 центрального элемента выбирается из условия минимальной сферической аберрации и составляет не более 30°.
Исходя из этого определяется угол преломления b 0 и радиус кривизны центрального элемента. Далее рассчитываются первый, второй и все последующие оптические элементы линзы. При этом определяется величина ti для каждого элемента линзы и она сравнивается с t з, заданной по конструктивным и техническим соображениям. Величина ti должна совпадать с t з в пределах ±1 – 2%. Следовательно, задача оптического расчёта линзы сводится к нахождению такой высоты оптического элемента или угла φ i, при которых соблюдается эти условия.
Если вести расчёт из предположения, что предыдущий элемент линзы рассчитан и известны все его параметры (они имеют индекс «0»), то пользуясь рисунком 4, можно написать ряд выражений, связывающих фокусное расстояние f, размеры элемента и показатель преломления стекла n с углами входа, преломления и выхода фокальных лучей. При этом предполагается, что фокусное расстояние центрального элемента со сферической преломляющей поверхность равно фокусному расстоянию f всей линзы. Для определения f необходимо задаться диаметром D л линзы и углом её охвата 2φa. Тогда можно определить радиус кривизны R и толщину t 0 центрального элемента.
Пусть нам заданы f, n, φл, и t з линзы с прямым несущим слоем и толщиной t. Тогда можно предположить следующую последовательность операций ее оптического расчёта:
1.Задаёмся высотой элемента (координатой Х) и определяем точку М вершины элемента.
2.Определяем угловую координату точки М и угол падения фокального луча в эту точку:
 , α=φ. , α=φ.
| (1) |
3. Определяем угол преломления луча в точке М:
 . .
| (2) |
4. Рассчитываем координату точки М´:
| X´ = X+ t 1tg b, Z´ = f + t. | (3) |
5.Рассчитываем угол преломления b ´ на внешней преломляющей грани, обеспечивающий отклонение осевого луча параллельно оптической оси:
 , ,  , ,

| (4) |
или

| (5) |
Поделив обе части равенства (5) на  , получим
, получим
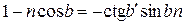 ,
,
Откуда окончательно
 . .
| (6) |
6. Рассчитываем величину выступа элемента t 1 над несущим слоем. Она находится из решения косоугольного треугольника М´М0´М´´ сторона которого М0´М´´ определяется с помощью теоремы синусов:
 . .
| (7) |
Углы  и
и  и сторона М 0´ М ´ находятся из очевидных выражений:
и сторона М 0´ М ´ находятся из очевидных выражений:
М 0´ М ´ = (X ´- X 0´),
 ,
,
где  – как углы со взаимно перпендикулярными сторонами.
– как углы со взаимно перпендикулярными сторонами.
Подставив найденные значения углов и стороны в формулу (7), получим:
 . .
| (8) |
Зная отрезок М0´М´´можно найти:
 . .
| (9) |
7.Рассчитываем радиус кривизны второй преломляющей поверхности элемента. Для этого можно спроектировать отрезки Oц М ´ и Oц М ´´ на ось Z, откуда:
 . .
| (10) |
8. Рассчитываем координаты центра кривизны:
| X ц = X ´ - R sin b ´, Z ц = (f + t 1) - R cos b ´. | (11) |
9.Рассчитываем координаты точки М 1´:
| X 1´ = X 0´ + t 1 tg b 0, Z 1´ = Z 0´ + t 1, | (12) |






