Матрица  называется обратной к квадратной матрице
называется обратной к квадратной матрице  , если
, если
 ,
,
где  - единичная матрица, имеющая тот же порядок, что и матрица
- единичная матрица, имеющая тот же порядок, что и матрица  . Обратная матрица существует только в том случае, если
. Обратная матрица существует только в том случае, если  , и ее элементы находятся по формуле
, и ее элементы находятся по формуле
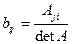 ,
,
где  - алгебраическое дополнение к элементу
- алгебраическое дополнение к элементу  .
.
Внимание! Алгебраические дополнения вычисляются к элементам строки, а записываются в столбец.
Если  , то матрица
, то матрица  называется вырожденной, в противном случае невырожденной, т.е. обратная матрица существует только для невырожденных матриц.
называется вырожденной, в противном случае невырожденной, т.е. обратная матрица существует только для невырожденных матриц.
Обозначается обратная матрица  , т.е.
, т.е.
 ,
,
при этом ее определитель 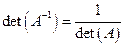 .
.
Для невырожденных матриц  и
и  выполнены соотношения
выполнены соотношения
 ,
,
 .
.
Введение обратной матрицы позволяет решать матричные уравнения. В конечном счете, матричные уравнения сводятся к двум простейшим уравнениям:
 или
или  .
.
Если матрица  - квадратная, невырожденная, то эти уравнения имеют единственное решение, которое можно получить с помощью обратной матрицы. Так как при умножении матриц коммутативный закон не выполняется, указанные уравнения имеют различные решения.
- квадратная, невырожденная, то эти уравнения имеют единственное решение, которое можно получить с помощью обратной матрицы. Так как при умножении матриц коммутативный закон не выполняется, указанные уравнения имеют различные решения.
При поиске решения первое из уравнений надо умножать на обратную матрицу  слева, а второе справа, т.е.
слева, а второе справа, т.е.
 , (5)
, (5)
 . (6)
. (6)
►Пример 5. Найти решение матричного уравнения  , то есть определить матрицу
, то есть определить матрицу  , если
, если  ;
; 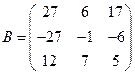 .
.
Решение.
Решение в матричном виде определяется формулой (5), т.е.  , если матрица
, если матрица  невырожденная. Вычислим определитель матрицы
невырожденная. Вычислим определитель матрицы  :
:
 .
.
Следовательно, матрица  невырожденная, и для нее существует обратная матрица. Проведем вычисления, необходимые для построения обратной матрицы. Вычислим алгебраические дополнения:
невырожденная, и для нее существует обратная матрица. Проведем вычисления, необходимые для построения обратной матрицы. Вычислим алгебраические дополнения:


Составим обратную матрицу  и найдем неизвестную матрицу
и найдем неизвестную матрицу  .
.
 ,
,  . ◄
. ◄
При вычислениях множитель  лучше оставлять перед матрицей и проводить умножение полученной матрицы на него на последнем этапе вычислений.
лучше оставлять перед матрицей и проводить умножение полученной матрицы на него на последнем этапе вычислений.
Упражнения.
1. Для заданных матриц найти обратную матрицу:
а)  ; б)
; б)  ;в)
;в) 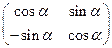 ;г)
;г)  ;д)
;д)  .
.
Ответы:
а) 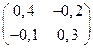 ; б)
; б)  ; в)
; в)  ; г)
; г)  ;
;
д) 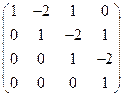 .
.
2. Найти неизвестную матрицу из уравнений:
а)  ; б)
; б) 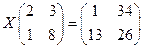 ;в)
;в)  ;
;
г)  ; д)
; д)  .
.
Ответы: а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  ; д)
; д)  .
.
Ранг матрицы
Рангом матрицы  (обозначение:
(обозначение:  ) называется порядок отличного от нуля минора этой матрицы при условии, что все ее миноры более высоких порядков равны нулю. Минор наивысшего порядка, отличный от нуля, называется базисным минором или просто б азисом. Матрица может иметь несколько различных базисов. Для определения базиса над матрицей производят элементарные преобразования, при которых ранг матрицы не изменяется.
) называется порядок отличного от нуля минора этой матрицы при условии, что все ее миноры более высоких порядков равны нулю. Минор наивысшего порядка, отличный от нуля, называется базисным минором или просто б азисом. Матрица может иметь несколько различных базисов. Для определения базиса над матрицей производят элементарные преобразования, при которых ранг матрицы не изменяется.
К элементарным преобразованиям матрицы относятся:
- транспонирование;
- удаление или добавление строки (столбца), состоящей из нулей;
- умножение строки (столбца) на число, отличное от нуля;
- перестановка строк (столбцов);
-прибавление к элементам какой-либо строки элементов другой строки, умноженных на постоянное число (то же самое для столбцов).
Выполняя элементарные преобразования над матрицей, получаем другую матрицу, называемую эквивалентной. Переход от исходной матрицы к эквивалентной будем обозначать символом  .
.
Используя выше перечисленные действия, матрицу можно преобразовать к треугольному виду, что позволяет легко определить ее ранг.
►Пример 7. Найти ранг матрицы  .
.
Решение.
Преобразуем матрицу:


Минор  , а все миноры четвертого порядка равны нулю, т.к. содержат нулевую строку. Следовательно,
, а все миноры четвертого порядка равны нулю, т.к. содержат нулевую строку. Следовательно,  . ◄
. ◄
При преобразовании матрицы мы проводили операции только со строками и по определенному алгоритму. Этот метод стандартный, но не является обязательным.
Упражнения.
1. Найти ранг матриц:
а)  ; б)
; б)  ;
;
в)  ; г)
; г)  . Ответы: а) 4; б) 2; в) 4; г) 3.
. Ответы: а) 4; б) 2; в) 4; г) 3.
Системы линейных уравнений. Основные понятия
Системой  линейных уравнений с
линейных уравнений с  неизвестными
неизвестными 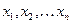 (линейной системой) называется система вида
(линейной системой) называется система вида
 (7)
(7)
где  − заданные числа. Числа
− заданные числа. Числа  называются коэффициентами системы, а числа
называются коэффициентами системы, а числа 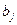 - свободными членами.
- свободными членами.
Линейная система называется однородно й, если все свободные члены равны нулю, т.е.
 (8)
(8)
В противном случае линейная система называется неоднородной.
Решением системы (7) называется упорядоченная совокупность  чисел:
чисел:
 , (9)
, (9)
при подстановке которых вместо 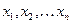 каждое уравнение системы обращается в тождество.
каждое уравнение системы обращается в тождество.
Система, имеющая хотя бы одно решение, называется совместной, а система, не имеющая ни одного решения, - несовместной. Совместная система называется определенной, если она имеет единственное решение, и неопределенной, если она имеет более одного решения.
Однородная система (8) всегда совместна, так как она имеет очевидное решение:  . Нулевое решение однородной системы называется тривиальным.
. Нулевое решение однородной системы называется тривиальным.
Две системы называются равносильными или эквивалентными, если любое решение одной из них является также решением и другой, и обратно, т.е. они имеют одно и то же множество решений. В частности, любые две несовместные системы являются эквивалентными.
Линейную систему можно записать в матричной форме. Введем матрицы
 – матрица коэффициентов при неизвестных,
– матрица коэффициентов при неизвестных,
 - матрица-столбец свободных членов,
- матрица-столбец свободных членов,
 - матрица-столбец неизвестных.
- матрица-столбец неизвестных.
Тогда систему (7) можно записать в виде матричного уравнения
 ,
,
а решение (9) в виде матрицы-столбца  .
.
Матрица коэффициентов

называется основной матрицей системы. Матрица, составленная из коэффициентов и свободных членов,
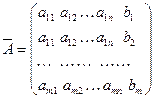
называется расширенной матрицей системы.
Выражение «решить систему» означает: выяснить, совместна или несовместна система, а в случае совместности – найти все ее решения.






