При анализе различных цепей часто возникает необходимость комплексные сопротивления и проводимости представить электрическими моделями – схемами замещения.
 |
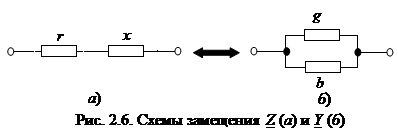Участок цепи с сопротивлением Z = r + jx можно представить моделью в виде последовательной схемы из двух элементов r и x (сопротивления складываются при последовательном соединении), изображенной на рис. 2.6, а. Этот же участок цепи можно представить параллельной схемой (рис. 2.6, б), если известна комплексная проводимость участка Y = g + jb (проводимости складываются при параллельном соединении элементов).
Если считать, что Z и Y параметры одного и того же участка цепи, то можно утверждать, что схемы на рис. 2.6 эквивалентные. Эквивалентными цепями называются такие, у которых напряжения и токи на внешних одноименных полюсах при заданных условиях совпадают, т.е. внешние электрические параметры равны. Следовательно, для этих схем должно выполняться условие эквивалентности:
, т. е.
(2.23 )
Из выражений (2.23) можно определить связь между резистивными и реактивными составляющими комплексного сопротивления и комплексной проводимости участка цепи (2.24):
(2.24)
Отметим, реактивные составляющие при преобразовании меняют знак, а также каждая составляющая r и x зависит от g и b и наоборот – g и b зависят от r и x.
КОМПЛЕКСНЫЕ СОПРОТИВЛЕНИЯ И ПРОВОДИМОСТИ ИДЕАЛИЗИРОВАННЫХ ЭЛЕМЕНТОВ (R, L, C)
Для определения комплексных параметров можно воспользоваться методом комплексных амплитуд. Заменим мгновенные значения гармонических напряжений и токов их комплексными изображениями
. (2.25)
Запишем выражения, связывающие между собой напряжения и токи в сопротивлении R (1.6), в индуктивности L (1.8) и в емкости C (1.11), для мгновенных комплексных значений (2.25).
Резистивный элемент R
 |
По этому выражению можно найти комплексные сопротивление ZR (j ω)и проводимость Y R (j ω)резистивного элемента
(2.26)
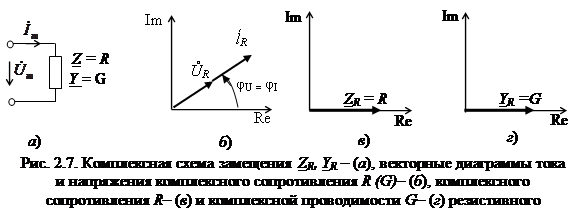
Сравнивая выражения (2.26) с (2.13), (2.14), (2.22), устанавливаем, что комплексные сопротивление и проводимость являются чисто резистивными (x = b = 0) (рис. 2.7, в, г), а модули равны параметрам R иG резистивного элемента (рис. 2.7, а). Следовательно, фазовый сдвиг φZ = φU – φI = – φY = 0 равен нулю, т.е. напряжение и ток в сопротивлении совпадают по фазе (рис. 2.7, б).
Комплексная схема замещения резистивного элемента (рис. 2.7, а) имеет такой же вид, как и схема замещения этого элемента для мгновенных значений (см. рис. 1.7) и отличается от последней комплексными изображениями ŮR и İR.
Индуктивный элемент L
Подставим комплексные изображения (2.25) в выражение (1.8).
.
После преобразования получим соотношение, связывающее между собой комплексные амплитуды напряжения и тока в индуктивности: 
Оно позволяет получить выражения комплексных сопротивления ZL (j ω)и проводимости YL (j ω)индуктивности:
(2.27)
Сравнивая (2.27) с показательной (2.13), алгебраической (2.14), (2.22) формами записи комплексных сопротивления и проводимости можно сделать вывод о характере комплексного сопротивления и проводимости индуктивности:
1. Комплексные сопротивление и проводимость индуктивности чисто реактивные и зависят от частоты (прямо пропорционально и обратно пропорционально соответственно)
ZL (j ω) =j ω L, YL (j ω) = – 1/ ω L; (2.28)
2. Резистивные составляющие равны нулю:
rL = gl = 0;
3. Разность фаз между напряжением и током равна π /2, т.е. напряжение на индуктивности опережает ток на 900:
 |
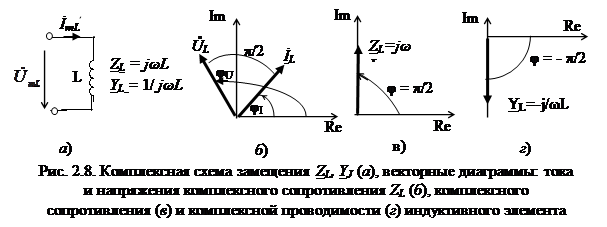φZL = φU - φI = π /2 = – φYL (рис. 2.8, в, г)
Емкостной элемент C
Если подставить комплексные изображения (2.22) в выражение (1.11) и произвести преобразования, как и для индуктивности, то получатся выражения комплексных сопротивления ZC (j ω) и проводимости YC (j ω) емкости.
(2.29)
Сравнивая (2.29) с показательной (2.13), алгебраической (2.14), (2.22) формами записи комплексных сопротивления и проводимости можно сделать вывод о характере комплексного сопротивления и проводимости емкости.
1. Комплексные сопротивление и проводимость емкости чисто реактивные и зависят от частоты (обратно пропорционально и прямо пропорционально соответственно)
ZL (j ω) =jωL, YL (j ω) = –1 /ωL; (2.30
2. Резистивные составляющие равны нулю: rC = gC = 0 (рис. 2.9, в, г);
3. Разность фаз между напряжением и током равна – π/2, т.е. напряжение на емкости отстает от тока на 900: φZL = φU - φI = – π/2 = – φYL (рис. 2.9, в, г).
