При составлении уравнений с использованием метода контурных токов, необходимо учитывать включение индуктивно-связанных катушек относительно контурных токов.
Запишем уравнения для контурных токов (рис. 4.29).

Рисунок 4.29 -
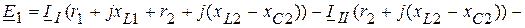

 .
.

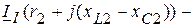

 .
.


 .
.
Таким образом, сопротивление взаимной индуктивности входит со знаком плюс или минус в зависимости от того совпадают или не совпадают по отношению к одноименным зажимам направления обхода (или контурного тока) одного элемента и тока в другом элементе.
Пример 4.19. Рассчитать состояние цепи, приведенной на рисунке 4.30 и рассмотренной в примере 4.17, методом контурных токов.
Решение

Рисунок 4.30 – Схема для расчета контурных комплексных токов
1. Приведенная электрическая схема состоит из четырех ветвей, причем катушки в первой  и второй
и второй  ветвях включены встречно, а контурные токи
ветвях включены встречно, а контурные токи  и
и  направлены навстречу друг другу. Катушки в третьей
направлены навстречу друг другу. Катушки в третьей  и четвертой
и четвертой  ветвях включены согласно, а контурные токи
ветвях включены согласно, а контурные токи  и
и  направлены навстречу друг другу
направлены навстречу друг другу
2.1. Составляем уравнения для определения контурных токов:

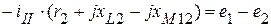 (I контур);
(I контур);

 (II контур);
(II контур);
 (III контур).
(III контур).
Записываем уравнения в символической форме
 ;
;
 ;
;
 .
.
2.2. Подставляем числовые значения и решаем систему уравнений:
2.2.1. Контурные сопротивления в символической форме
 Ом;
Ом;
 Ом;
Ом;
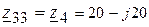 Ом.
Ом.
Сумма сопротивлений, принадлежащих нескольким контурам
 Ом;
Ом;
 Ом.
Ом.
Контурные ЭДС
 В;
В;
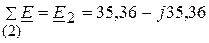 В;
В;
 В.
В.
2.2.2. После подстановки цифровых данных система имеет вид

2.2.3. Решая данную систему уравнений, определяем контурные токи:
 А;
А;
 А;
А;
 А.
А.
2.2.4. Определяем токи в ветвях электрической цепи, приведенной на рисунке 4.31.
 А;
А;
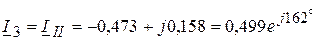 А;
А;
 А;
А;
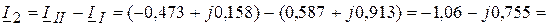
 А.
А.
Токи в ветвях, рассчитанные в примерах 4.19 и 4.17, совпадают.
Пример 4.20. Рассчитать состояние цепи, приведенной на рисунке 4.28 и рассмотренной в примере 4.18, методом контурных токов.
Решение
1. Вычертим схему для определения комплексов тока (рис. 4.31).

Рисунок 4.31 – Схема для расчета комплексных токов
2.1. Составляем уравнения для определения контурных токов:

 (I контур);
(I контур);

 (II контур).
(II контур).
Записываем уравнения в символической форме
 ;
;
 .
.
2.2. Подставляем числовые значения и решаем систему уравнений:
2.2.1. Контурные сопротивления в символической форме
 Ом;
Ом;
 Ом.
Ом.
Сумма сопротивлений, принадлежащих нескольким контурам
 Ом.
Ом.
Контурные ЭДС  В;
В;
 В.
В.
2.2.2. После подстановки цифровых данных система имеет вид

2.2.3. Решая данную систему уравнений, определяем контурные токи:
 А;
А;
 А.
А.
2.2.4. Определяем токи в ветвях электрической цепи, приведенной на рисунке 4.31.
 А;
А;
 А;
А;

 А.
А.
Токи в ветвях, рассчитанные в примерах 4.20 и 4.18, совпадают.
4.4.3. Мощность в разветвленных цепях при наличии взаимной индуктивности
Пример 4.21. Составим баланс мощностей для электрической цепи, представленной на рисунке 4.27 и рассмотренной в примерах 4.17 и 4.19.
Из примера 4.17, следует, что комплексы напряжения на источниках питания  В,
В, 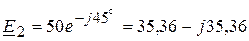 В,
В, 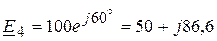 В, а комплексы токов
В, а комплексы токов  А;
А;  А;
А;  А;
А;  А.
А.
1. Определяем активную и реактивную мощности, генерируемые источниками питания.

 ВА,
ВА,

 ВА,
ВА,

 ВА.
ВА.
Суммарная комплексная мощность, генерируемая источниками питания

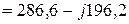 ВА.
ВА.
Таким образом, суммарная активная  и суммарная реактивная
и суммарная реактивная  мощности равны
мощности равны  Вт,
Вт,  ВАр.
ВАр.
2. Определяем активную мощность, потребляемую потребителями
 .
.
На резистивных элементах
 Вт,
Вт,
 Вт,
Вт,
 Вт,
Вт,
 Вт.
Вт.
Суммарная активная мощность
 Вт.
Вт.
3. Комплексная мощность, передаваемая электромагнитным путем от первой катушки ко второй  и от третьей катушки к четвертой
и от третьей катушки к четвертой 
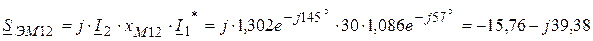
 Вт,
Вт,  ВАр
ВАр

 Вт,
Вт,  ВАр.
ВАр.
4. Определяем реактивную мощность, потребляемую потребителями
 .
.
На резистивных элементах
 ВАр,
ВАр,
 ВАр,
ВАр,
 ВАр,
ВАр,
 ВАр.
ВАр.
Суммарная активная мощность
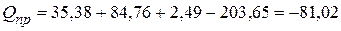 ВАр.
ВАр.
5. Баланс реактивных мощностей

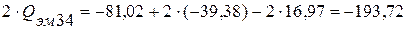 ВАр.
ВАр.
4.5. Эквивалентная замена (развязка) индуктивной связи
Анализ и расчет цепей в ряде случаев упрощается, если часть схемы, содержащую индуктивную связь заменить эквивалентной схемой без индуктивной связи. Этот процесс называется эквивалентной заменой, устранением или развязкой индуктивной связи.
На рисунке 4.32,а приведена часть электрической цепи, подсоединенная к узлу 3 и содержащая индуктивно связанные катушки, когда элементы подключены к узлу одноименными зажимами. Используя первый и второй законы Кирхгофа, запишем уравнения, описывающие состояние приведенной части цепи.

Рисунок 4.32 – Развязка индуктивной связи при подключении элементов одноименными зажимами
Применяя первый закон Кирхгофа для узла 3, имеем  .
.
Применяя второй закон Кирхгофа, определяем напряжение между зажимами 1 и 3, имеем
 .
.
Применяя второй закон Кирхгофа, определяем напряжение между зажимами 2 и 3, имеем
 .
.
Так как  , тогда напряжение
, тогда напряжение  соответственно равно
соответственно равно


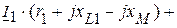
 .
.
Так как  , тогда напряжение
, тогда напряжение  соответственно равно
соответственно равно


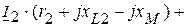
 .
.
Полученной системе уравнений соответствует схема, приведенная на рисунке 4.32 б. Она не имеет индуктивных связей, т.к. описывается одинаковой системой уравнений. Тогда, полученная система уравнений эквивалентна приведенной выше и, следовательно, описывает состояние цепи.
Таким образом, для устранения индуктивной связи необходимо к катушкам  и
и  , подключенных к одному узлу одноименными зажимами, добавить
, подключенных к одному узлу одноименными зажимами, добавить  , а перед узлом 3 включить новый элемент
, а перед узлом 3 включить новый элемент  .
.
Если индуктивно связанные элементы, подсоединены к узлу разноименными зажимами (рис. 4.33,а), то для устранения индуктивной связи необходимо к катушкам  и
и  добавить
добавить  , а перед узлом 3 включить новый элемент
, а перед узлом 3 включить новый элемент  (рис. 4.33,б).
(рис. 4.33,б).

Рисунок 4.34 – Развязка индуктивной связи при подключении элементов разноименными зажимами
В этом случае, напряжения  и
и  соответственно равны
соответственно равны

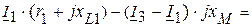
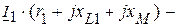
 ,
,



 .
.
Правило знаков: Если индуктивно связанные катушки подключены к одному узлу одноименными зажимами, то в эти ветви  вводится со знаком «-», а в общую ветвь – со знаком «+», и наоборот, если индуктивно связанные катушки подключены к одному узлу разноименными зажимами, то в эти ветви
вводится со знаком «-», а в общую ветвь – со знаком «+», и наоборот, если индуктивно связанные катушки подключены к одному узлу разноименными зажимами, то в эти ветви  вводится со знаком «+», а в общую ветвь – со знаком «-».
вводится со знаком «+», а в общую ветвь – со знаком «-».
Если индуктивно связанные ветви не имеют общего узла, то развязка индуктивной связи также возможна, однако в данном случае эквивалентная схема получается достаточно сложной и пользоваться ею обычно нецелесообразно.
Если индуктивно связанные элементы соединены трехлучевой звездой или треугольником (рис. 4. 35), то применяя последовательно рассмотренной способ замены, можно перейти к схемам без индуктивных связей.

Рисунок 4.35 – Развязка треугольника
Пример 4.23. Рассчитать токи в ветвях индуктивно-связанной цепи, приведенной на рисунке 4.29 и рассмотренной в примерах 4.18 и 4.20, используя эквивалентную замену индуктивных связей.
Решение
Используя приведенное выше правило для развязки индуктивных связей, получим эквивалентную схему (рис. 4.36) цепи, приведенной на рисунке 4.29

Рисунок 4.36 – Эквивалентная схема
1. Подготовим схему для расчета комплексов тока:
1.1. Формируем комплекс ЭДС источника питания:
 В.
В.
1.2. Формируем комплексные сопротивления ветвей:
 Ом;
Ом;
 Ом;
Ом;

 Ом.
Ом.
2. Определяем комплексное входное сопротивление цепи.
2.1. Параллельно соединенную вторую и третью ветви, заменяем эквивалентной и определяем сопротивление  :
:
 Ом.
Ом.
2.2. Комплексное входное сопротивление цепи
 Ом.
Ом.
3. Определяем комплексы токов.
3.1. Комплекс тока  :
:
 (А).
(А).
3.2. Определяем комплексы токов 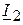 и
и  .
.
3.2.1. Комплексное напряжение  на зажимах второй и третьей ветви:
на зажимах второй и третьей ветви:
 (В).
(В).
3.2.2. Комплекс тока 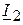 :
:
 (А).
(А).
3.2.3. Комплекс тока  :
:
 (А).
(А).
Токи в ветвях, рассчитанные в примерах 4.18, 4.20 и 4.23, совпадают.
Пример 4.24. Построим топографическую диаграмму цепи, приведенную на рисунке 4.37. Из примера 4.23, следует, что комплекс напряжения на источнике питания  (В), а комплексы токов в ветвях соответственно равны
(В), а комплексы токов в ветвях соответственно равны  (А),
(А),  (А),
(А), 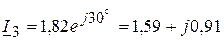 (А).
(А).
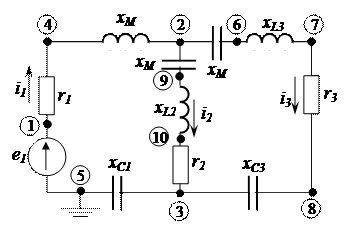
Рисунок 4.37 – Электрическая цепь
1. Принимаем потенциал точки 5 равным нулю:  В.
В.
2. Определяем комплекс потенциала точки 1:  В.
В.
3. Определяем комплекс потенциала точки 4:
 В.
В.
4. Определяем комплекс потенциала точки 2:
 В.
В.
5. Определяем комплекс потенциала точки 9:
 В.
В.
6. Определяем комплекс потенциала точки 10:
 В.
В.
7. Определяем комплекс потенциала точки 3:
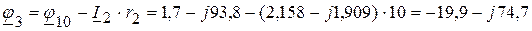 В.
В.
8. Осуществляем проверку комплекса точки 5:
 В.
В.
9. Определяем комплекс потенциала точки 6:
 В.
В.
10. Определяем комплекс потенциала точки 7:
 В.
В.
11. Определяем комплекс потенциала точки 8:
 В.
В.
12. Осуществляем проверку комплекса точки 3:
 В.
В.
13. Строим топографическую диаграмму (рис. 4.38). На рисунке 4.38 приведены также комплексы токов  ,
,  ,
,  .
.

Рисунок 4.38 – Топографическая диаграмма
4.6. Воздушный трансформатор
В электротехнике широко применяется передача энергии из одного контура в другой при помощи трансформаторов, которые могут иметь различное назначение, но чаще всего предназначены для изменения величины переменного напряжения. Надобность в таком изменении появляется, например, в случае, когда напряжение источника питания отличается от напряжения, которое требуется для приемника энергии. Трансформаторы состоят из двух или нескольких индуктивно связанных катушек или обмоток. Ограничимся рассмотрением простейшего двухобмоточного трансформатора без ферромагнитного сердечника. Такие трансформаторы чаще всего применяются при высоких частотах в связи, радио, а в ряде специальных измерительных устройств и при низкой частоте переменного тока.
Обмотка трансформатора, к которой подводится питание называется первичной, а обмотка, к которой подключается приемник энергии (нагрузка) – вторичной. Все величины, относящиеся к первичной обмотке, называют первичными и им приписывается индекс 1, а все величины, относящиеся ко вторичной обмотке, называют вторичными и им приписывается индекс 2. Цепи, в которые входят первичные и вторичные обмотки, называют соответственно первичными и вторичными цепями. Если пренебречь ёмкостью между витками обмоток трансформатора, то цепь, состоящую из двухобмоточного трансформатора и нагрузки, имеет схему, приведенную на рисунке 4.39

Рисунок 4.39 –Двухобмоточный трансформатор
Сопротивление первичной обмотки  , сопротивление вторичной –
, сопротивление вторичной –  , сопротивление нагрузки
, сопротивление нагрузки  .
.
Уравнения трансформатора при принятой полярности катушек и направлении токов имеют вид:
 ;
;
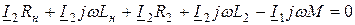 .
.
Этим уравнениям соответствует векторная диаграмма на рисунке 4.40. Начинаем построение диаграммы с вектора тока вторичной цепи  , т.к. именно этот ток может быть задан исходя из условий работы приемника.
, т.к. именно этот ток может быть задан исходя из условий работы приемника.
Откладываем относительно вектора  напряжения на активном и реактивном сопротивлениях нагрузки
напряжения на активном и реактивном сопротивлениях нагрузки  ,
, 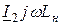 , а также напряжения на активном и реактивном сопротивлениях вторичной обмотки
, а также напряжения на активном и реактивном сопротивлениях вторичной обмотки  ,
,  . Суммарным вектором этих напряжений будет вектор напряжения взаимной индукции
. Суммарным вектором этих напряжений будет вектор напряжения взаимной индукции  . Таким образом, построены векторы всех напряжений вторичной цепи трансформатора. Для построения напряжений первичной цепи откладываем вектор тока первичной обмотки
. Таким образом, построены векторы всех напряжений вторичной цепи трансформатора. Для построения напряжений первичной цепи откладываем вектор тока первичной обмотки  (отстает от вектора
(отстает от вектора  на
на 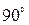 ). Относительно
). Относительно  откладываем напряжение на сопротивлениях первичной обмотки
откладываем напряжение на сопротивлениях первичной обмотки  ,
,  , а также вектор напряжения взаимной индукции
, а также вектор напряжения взаимной индукции 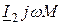 . Суммарным вектором последних трех напряжений есть вектор напряжения питания первичной обмотки
. Суммарным вектором последних трех напряжений есть вектор напряжения питания первичной обмотки  .
.

Рисунок 4.40 – Векторная диаграмма двухобмоточного трансформатора
без ферромагнитного сердечника
При подключении нагрузки ко вторичной обмотке изменяется сопротивление первичной цепи трансформатора. Для оценки вносимого (из вторичной цепи в первичную) сопротивления решим уравнения, составленные для трансформатора, относительно тока  .
.
В уравнении 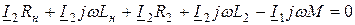 ,
,
заменим активное и индуктивное сопротивления нагрузки полным:
 ,
,
откуда
 .
.
Выражение для тока  подставим в уравнение
подставим в уравнение  :
:
 .
.
Из последнего уравнения выразим ток  :
:
 .
.
Если в знаменателе исключить активное и индуктивное сопротивления первичной обмотки, оставшееся выражение представляет собой вносимое сопротивление трансформатора:
 .
.
Разложим полное вносимое сопротивление  на активную и реактивную составляющие:
на активную и реактивную составляющие:

Сумму активных и реактивных сопротивлений вторичной цепи обозначают соответственно  и
и  :
:
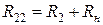 ;
; 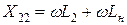 ,
,
при этом выражение для  -
-

 .
.
Действительная часть последнего выражения представляет собой активную составляющую вносимого сопротивления ( ), мнимая – реактивную (
), мнимая – реактивную ( ):
):
 ;
;  .
.
Окончательное выражение для  -
-
 .
.
Уравнение тока в первичной обмотке с учетом  -
-
 .
.
Последнее уравнение дает возможность представить схему замещения трансформатора (рис. 4.41) со стороны первичной обмотки как двухполюсник с сопротивлениями  и
и  .
.

Рисунок 4.41 – Схема замещения воздушного трансформатора
в виде двухполюсника
Вносимое активное сопротивление  всегда увеличивает активное сопротивление со стороны зажимов первичной обмотки по сравнению с величиной
всегда увеличивает активное сопротивление со стороны зажимов первичной обмотки по сравнению с величиной 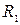 . Это обусловлено рассеиванием энергии в активном сопротивлении второго контура. Реактивное вносимое сопротивление
. Это обусловлено рассеиванием энергии в активном сопротивлении второго контура. Реактивное вносимое сопротивление  или увеличивает или уменьшает
или увеличивает или уменьшает 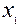 в зависимости от знака
в зависимости от знака  , который, в свою очередь, зависит от величины и характера
, который, в свою очередь, зависит от величины и характера  и его отношения с
и его отношения с 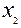 .
.
Пользуясь схемой замещения (рис. 4.41), рассмотрим условия передачи максимальной активной мощности во вторичную цепь трансформатора.
Условием передачи максимальной активной мощности от источника энергии к приемнику является равенство активного сопротивления приемника внутреннему активному сопротивлению источника, а также равенство нулю суммарного реактивного сопротивления приемника и внутреннего сопротивления источника.
Если в уравнении  сопротивления
сопротивления 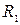 и
и  принять за внутренние сопротивления источника, а
принять за внутренние сопротивления источника, а  и
и  представить сопротивлениями приемника, условие передачи максимальной активной мощности определяется следующими соотношениями между сопротивлениями:
представить сопротивлениями приемника, условие передачи максимальной активной мощности определяется следующими соотношениями между сопротивлениями:
 ;
; 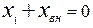
или
 ;
;  .
.
Последние соотношения можно получить, если предусмотреть возможность изменения реактивных сопротивлений  и
и  , а также коэффициента взаимной индукции
, а также коэффициента взаимной индукции  , причем достаточно иметь возможность изменять только
, причем достаточно иметь возможность изменять только  и
и  . Для этого в первичную и вторичную цепи трансформатора включают конденсаторы переменной емкости, как показано на рисунке 4.42. Для этой схемы
. Для этого в первичную и вторичную цепи трансформатора включают конденсаторы переменной емкости, как показано на рисунке 4.42. Для этой схемы
 ;
;  .
.
Изменяя значения  и
и  , можно добиться равенства в соотношении
, можно добиться равенства в соотношении  .
.

Рисунок 4.42 – Схема воздушного двухобмоточного трансформатора с конденсаторами  и
и  для изменения реактивных сопротивлений первичной и вторичной цепей
для изменения реактивных сопротивлений первичной и вторичной цепей
Но в отличие от цепи с источником энергии и приемником, в котором нет индуктивных связей, в трансформаторе для передачи максимальной активной мощности необходимо выполнение еще одного условия. Запишем уравнение  относительно
относительно  :
:
 .
.
В этом соотношении  имеет действительное(а не мнимое) значение при условии
имеет действительное(а не мнимое) значение при условии
 .
.
Если  , максимальная мощность не будет получена ни при каких значениях
, максимальная мощность не будет получена ни при каких значениях  и
и 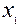 .
.
Схема трансформатора, состоящая из двух контуров с индуктивной связью, может быть заменена эквивалентной схемой замещения без индуктивных связей.
 Если соединить два нижних вывода схемы, как показано на рисунке 4.43, режим работы цепи не изменится.
Если соединить два нижних вывода схемы, как показано на рисунке 4.43, режим работы цепи не изменится.

Рисунок 4.43 – Схема двухобмоточного трансформатора с объединенным общим выводом
Части контуров с элементами  ,
,  и
и  ,
,  можно рассматривать как две индуктивно связанные ветви, присоединенные к одному узлу одноименными выводами, поэтому эквивалентная схема без взаимной индуктивности имеет вид, представленный на рисунке 4.44.
можно рассматривать как две индуктивно связанные ветви, присоединенные к одному узлу одноименными выводами, поэтому эквивалентная схема без взаимной индуктивности имеет вид, представленный на рисунке 4.44.

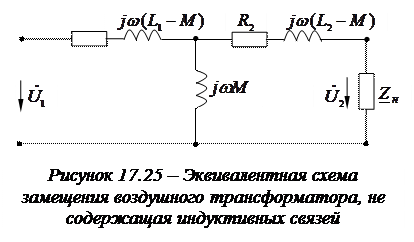
Рисунок 4.44 – Эквивалентная схема замещения воздушного трансформатора, не содержащая индуктивных связей
Такие схемы замещения называют четырехполюсными. Как и для трансформаторов с ферромагнитным сердечником, четырехполюсные схемы замещения широко используются при анализе работы и расчетах воздушных трансформаторов.
На практике часто в расчетах используют понятие идеального трансформатора, под которым понимают такой, у которого при любых условиях отношение комплексов первичного и вторичного напряжений равно отношению комплексов вторичного и первичного токов и равно постоянному комплексному числу N.

Комплексное число N называется коэффициентом трансформации и на практике обычно является вещественным числом. Идеальный трансформатор используют в качестве составного элемента схем замещения реальных трансформаторов.
Пусть ко вторичным (выходным) зажимам идеального трансформатора подключена нагрузка с сопротивлением Z 2. Тогда его входное сопротивление со стороны первичных зажимов будет:

т.е. оно в N 2раз отличается от Z 2. Это соотношение характеризует трансформацию сопротивлений. Если вторичные зажимы идеального трансформатора разомкнуты (ХХ, т.е. Z 2=∞), то и Z 1=∞, следовательно, в первичной цепи тока также не будет. Если вторичные зажимы закорочены (Z 2=0), то и Z 1=0, т.е. по первичной цепи также имеет место КЗ.
Для того чтобы трансформатор был идеальным нужно выполнить ряд требований, а именно: активные сопротивления первичной и вторичной обмоток должны равняться нулю, коэффициент связи равняться единице, а числа витков обеих обмоток стремиться к бесконечности.
Пример 4.25.
Пример 4.26.






