С помощью обратных тригонометрических функций можно решать простейшие тригонометрические уравнения:


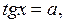  любое число; любое число; 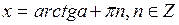
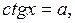  любое число; любое число; 
|
Уравнение  . Очевидно, что если
. Очевидно, что если  , то уравнение
, то уравнение
 (1)
(1)
не имеет решений, поскольку 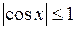 для любого х.
для любого х.
Пусть  . Надо найти все такие числа х, что
. Надо найти все такие числа х, что  . На отрезке
. На отрезке  существует в точности одно решение уравнени (1) – это число
существует в точности одно решение уравнени (1) – это число 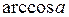 .
.
Косинус – четная функция, и, значит, на отрезке 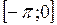 уравнение (1) также имеет в точности одно решение – число -
уравнение (1) также имеет в точности одно решение – число - 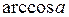 . Итак, уравнение
. Итак, уравнение  на отрезке
на отрезке  длиной 2p имеет два решения:
длиной 2p имеет два решения: 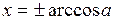 (совпадающие при а=1).
(совпадающие при а=1).
Вследствие периодичности функции  все остальные решения отличаются от этих на
все остальные решения отличаются от этих на 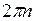
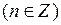 , т.е. формула корней уравнения (1) такова:
, т.е. формула корней уравнения (1) такова:
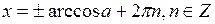 (2)
(2)
(Обратите внимание: этой формулой можно пользоваться только при  ).
).
При а=1 числа 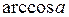 и -
и - 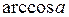 совпадают (они равны нулю), поэтому решение уравнения
совпадают (они равны нулю), поэтому решение уравнения  принято записывать в виде
принято записывать в виде 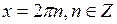 .
.
Особая форма записи решений уравнения (1) принята также для а=-1 и а=0:
 при
при 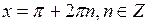
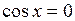 при
при  .
.
Уравнение  . Уравнение
. Уравнение
 (3)
(3)
не имеет решений при  , так как
, так как 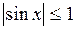 для любого х.
для любого х.
При  на отрезке
на отрезке  уравнение (3) имеет в точности одно решение
уравнение (3) имеет в точности одно решение  . На промежутке
. На промежутке 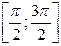 функция
функция  убывает и принимает все значения от -1 до 1. По теореме о корне уравнение (3) имеет и на этом отрезке один корень. Из рисунка видно, что этот корень есть число
убывает и принимает все значения от -1 до 1. По теореме о корне уравнение (3) имеет и на этом отрезке один корень. Из рисунка видно, что этот корень есть число 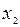 , равное
, равное  . Действительно,
. Действительно,  . Кроме того, поскольку
. Кроме того, поскольку  , имеем
, имеем  и
и  , т.е. число
, т.е. число 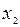 принадлежит отрезку
принадлежит отрезку  .
.
Итак, уравнение (3) на отрезке 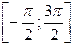 имеет два решения:
имеет два решения:  и
и  (совпадающие при
(совпадающие при  ). Учитывая, что период синуса равен
). Учитывая, что период синуса равен 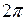 , получаем такие формулы для записи всех решений уравнения:
, получаем такие формулы для записи всех решений уравнения:
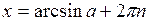 (4)
(4)
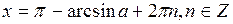 (5)
(5)
Удобно решения уравнения (3) записывать не двумя, а одной формулой:
 (6).
(6).
Нетрудно убедиться, что при четных 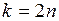 из формулы (6) находим все решения, записанные формулой (4); при нечетных
из формулы (6) находим все решения, записанные формулой (4); при нечетных  – решения, записываемые формулой (5).
– решения, записываемые формулой (5).
Если а=1, точисла  и
и  совпадают, поэтому решение уравнения
совпадают, поэтому решение уравнения  принято записывать так:
принято записывать так: 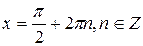 .
.
При а=-1 и а=0 принята следующая запись решений:
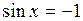 при
при 
 при
при 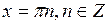 .
.
Уравнение 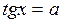 .
.
При любом 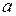 на интервале
на интервале  имеется ровно одно такое число х, что
имеется ровно одно такое число х, что 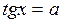 , - это
, - это  .
.
Поэтому уравнение
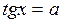 (7)
(7)
имеет на интервале  длиной p единственный корень.
длиной p единственный корень.
Функция тангенс имеет период p.
Следовательно, остальные корни уравнения (7) отличаются от найденного на  , т.е.
, т.е.
 (8)
(8)
Уравнение 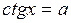 .
.
При любом 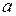 на интервале
на интервале 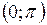 имеется ровно одно такое число х, что
имеется ровно одно такое число х, что 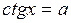 , - это
, - это 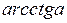 .
.
Поэтому уравнение
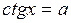 (9)
(9)
имеет на интервале 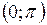 длиной p единственный корень.
длиной p единственный корень.
Функция котангенс имеет период p.
Следовательно, остальные корни уравнения (9) отличаются от найденного на  , т.е.
, т.е.
 (10)
(10)
Тригонометрические неравенства
| Вид неравенства | Множество решений неравенства ( ) )
|
 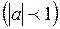
| 
|
 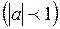
| 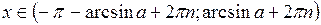
|
 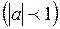
| 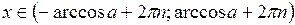
|
 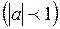
| 
|

| 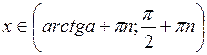
|
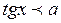
| 
|
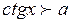
| 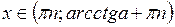
|
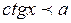
| 
|
Вывод
Слово «тригонометрия» искусственно составлено из греческих слов: «тригонон» – треугольник и «метрезис» - измерение (соответствующим русским термином было «треугольникомерие»). Основная задача тригонометрии состоит в решении треугольников, т.е. в вычислении неизвестных величин треугольника по данным значениям других его величин. Так, в тригонометрии решают задачу о вычислении углов треугольника по данным его сторонам, задачу о вычислении сторон треугольника – по площади и двум углам и т.д. Так как любую вычислительную задачу геометрии можно свести к решению треугольников, то тригонометрия охватывает своими применениями всю планиметрию и стереометрию и широко применяется во всех отделах естествознания и техники.
Углы произвольного треугольника нельзя связать непосредственно с его сторонами с помощью алгебраических соотношений. Поэтому тригонометрия вводит в рассмотрение, кроме самих углов, еще новые количества, так называемые тригонометрические величины. Эти величины уже можно связать со сторонами треугольника простыми алгебраическими соотношениями. С другой стороны, по данному углу можно вычислить соответствующее значение тригонометрической величины, и обратно. Правда, эти вычисления требуют длительных и утомительных расчетов, но эта работа проделана раз и навсегда, и закреплена в таблицах.
Значение каждой тригонометрический величины изменяется с изменением угла, тригонометрическая величина есть функция угла. Отсюда наименование: тригонометрические функции.
Между различными тригонометрическими функциями существуют важные зависимости. Использование их позволяет сокращать и облегчать вычисления.
Список литературы:
1. Математика. В.Т.Лисичкин, И.Л.Соловейчик. Москва, «Высшая школа», 1991г.
2. Алгебра и начала анализа 10-11. Под редакцией А.Н.Колмогорова. Москва, «Просвещение», 1991г.
3. Алгебра и начала анализа, ч.1. Под редакцией Г.Н.Яковлева. Москва, «Наука», 1981г.
4. Справочник по математике для средних учебных заведений. А.Г.Цыпкин. Москва, «Наука», 1988г.
5. Справочник по элементарной математике. М.Я.Выгодский. Москва, Физматгиз, 1962г.
6. Практические занятия по математике. Н.В.Богомолов. Москва, «Высшая школа», 1990г.
7. Уроки по курсу «Алгебра и начала анализа – 10». М.П.Нечаев. Москва, «5 за задания», 2007г.
8. Математика және Физика. Ғылыми - әдістемелік журнал №4-2008жыл.






