МГУ им. М.В. Ломоносова, Геологический Факультет
Кафедра геофизических методов исследования земной коры
Практикум по электроразведке (5 курс)
Построение и S - интерпретация кривых МТЗ
Практическое задание
В рамках настоящей работы нужно выполнить сокращенный вариант обработки и интерпретации данных МТЗ. Исходными являются записи МТЗ, относящиеся к четырем точкам регионального профиля (шаг по профилю 20 км) и априорная геолого-геофизическая информация. Результатом выполнения задачи должен стать геоэлектрический разрез по этому профилю. При выполнении данной работы необходимо сделать следующее:
1. Для первой точки МТЗ с помощью программы СORRECT выполнить второй этап обработки данных МТЗ - построить сглаженные частотные зависимости компонент тензора импеданса (4 амплитудных и 4 фазовых кривых, а также эффективные кривые) (см. раздел 4 данной разработки).
2. С помощью программы MTS-PROFILE выполнить анализ полученных кривых 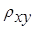 ,
,  ,
,  и определить, какие из них наименее искажены влиянием приповерхностных неоднородностей (см. раздел 5).
и определить, какие из них наименее искажены влиянием приповерхностных неоднородностей (см. раздел 5).
3. По программе MTS-SI провести контролируемую трансформацию неискаженных кривых с целью получения кривых  , отражающих нарастание интегральной проводимости с глубиной (см. раздел 6).
, отражающих нарастание интегральной проводимости с глубиной (см. раздел 6).
4. Для каждой точки зондирования по полученной кривой  с учетом априорной информации определить параметры геоэлектрического разреза (сопротивления и мощности слоев) (см. раздел 7). По результатам интерпретации кривых построить геоэлектрический разрез по профилю.
с учетом априорной информации определить параметры геоэлектрического разреза (сопротивления и мощности слоев) (см. раздел 7). По результатам интерпретации кривых построить геоэлектрический разрез по профилю.
Программы для работы с данными находятся в каталоге C:\STUDENTS, сами файлы данных и файл с априорной информацией read_me - в каталоге C:\STUDENTS\N, где N - номер вашего варианта.
Тензор импеданса
Возникновение метода магнитотеллурического зондирования (МТЗ) связано с именем А.Н. Тихонова. В 1950 году им было показано, что отношение ортогональных горизонтальных электрических и магнитных компонент магнитотеллурического поля, получившее название импеданса  , зависит от частоты и свойств среды, но не зависит от источника.
, зависит от частоты и свойств среды, но не зависит от источника.
Первоначально использовалась горизонтально-слоистая модель Земли (модель Тихонова - Каньяра), в которой импеданс  может быть определен на основе полевых данных как по формуле
может быть определен на основе полевых данных как по формуле  , так и по формуле
, так и по формуле  , где
, где  ,
, 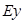 ,
,  и
и  - комплексные амплитуды соответствующих компонент электромагнитного поля. Однако практика очень скоро показала, что в районах с горизонтально-неоднородным строением среды импеданс
- комплексные амплитуды соответствующих компонент электромагнитного поля. Однако практика очень скоро показала, что в районах с горизонтально-неоднородным строением среды импеданс  зависит от ориентации установки. М.Н. Бердичевским и Т. Кантуэллом было предложено перейти от скалярного импеданса к тензору импеданса
зависит от ориентации установки. М.Н. Бердичевским и Т. Кантуэллом было предложено перейти от скалярного импеданса к тензору импеданса
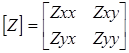
Тогда горизонтальные компоненты электрического и магнитного полей связаны соотношениями:
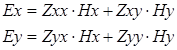 (1.1)
(1.1)
Компоненты тензора  и
и  называются главными, и именно по ним строятся кривые МТЗ. Компоненты
называются главными, и именно по ним строятся кривые МТЗ. Компоненты  и
и  называются дополнительными, для горизонтально-слоистой среды они равны нулю. Кроме того, при интерпретации данных МТЗ часто используется такая величина, как эффективный импеданс
называются дополнительными, для горизонтально-слоистой среды они равны нулю. Кроме того, при интерпретации данных МТЗ часто используется такая величина, как эффективный импеданс
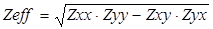
Замечательным свойством эффективного импеданса является то, что он является инвариантной величиной, т.е. не меняется при повороте системы координат.
Для последующего анализа удобно пересчитать кривые компонент тензора импеданса в соответствующие кривые кажущегося сопротивления по формулам
 ,
,  ,
,  (1.2)
(1.2)
Кривые кажущегося сопротивления можно дополнить фазовыми кривыми
 ,
,  ,
,  (1.3)
(1.3)
2. Первый этап обработки данных МТЗ
При проведении полевых работ с помощью цифровых электроразведочных станций (ЦЭС-2, ЦЭС-М, ЦАИС и др.), как правило, регистрируются вариации пяти компонент МТ-поля - двух горизонтальны компонент электрического поля (Ех, Еу) и трех компонент магнитного поля (Hх, Hу, Hz). Компонента Hz при определении тензора импеданса не используется, однако дает полезную информацию о горизонтальной неоднородности разреза.
Особенностью метода МТЗ по отношению к другим методам зондирования на постоянном и переменном токе является трудоемкий процесс обработки полевых материалов, предшествующий построению кривых зондирования. Целью обработки является разделение естественного электромагнитного поля Земли, имеющего случайный характер, на гармонические составляющие, по которым находятся компоненты тензора импеданса для набора соответствующих частот.
 Рис. 1. Результаты первого этапа обработки МТ-данных (компонента
Рис. 1. Результаты первого этапа обработки МТ-данных (компонента 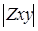 ). ).
|
Выделение гармонической составляющей сигнала (узкополосную фильтрацию) в частотной области можно представить как умножение спектра сигнала на частотную характеристику фильтра. Однако удобнее осуществлять узкополосную фильтрацию не в частотной, а непосредственно во временной области. При этом, согласно теореме о свертке, умножение в частотной заменяется во временной облас-ти сверткой сигнала с импульсной харак-теристикой фильтра.
В результате свертки мы находим значения гармони-ческих составляю-щих каждой компо-ненты электромаг-нитного поля для различных промежут-ков времени. Под-ставляя эти значения в импедансное соот-ношение (1.1), полу-чаем переопреде-ленную систему уравнений относительно компонент тензора импеданса, которая решается методом наименьших квадратов. Таким образом, для каждого участка записи МТ-поля получаем оценки значений компонент тензора импеданса. Разбивая всю запись на несколько участков, мы получаем оценки компонент тензора импеданса на каждом периоде (рис. 1). По этим оценкам можно определить среднее значение и среднее квадратическое отклонение компонент  для данного периода.
для данного периода.
Большинство оценок тензора импеданса группируется вблизи среднего значения. В то же время некоторые из них, отвечающие промежуткам времени с высоким уровнем помех, могут сильно отличаться от среднего значения.
Сглаживающие кубические сплайны
Задача о построении гладкой зависимости по результатам эксперимента является общей для многих разделов геофизики и других естественных наук. Она представляет собой обратную задачу, при решении которой применяется метод регуляризации. В этой задаче требуется провести кривую (сплайн) через облако полевых данных так, чтобы эта кривая, с одной стороны, проходила как можно ближе к средним для каждого периода значениям, а с другой стороны, удовлетворяла некоторому требованию (априорной информации). В качестве априорной информации принимается условие максимальной гладкости проводимой кривой частотной зависимости.
Сглаживающий кубический сплайн - это гладкая функция, на каждом отрезке представляющая собой многочлен третьей степени:
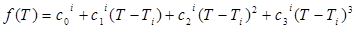 , где
, где 
В узлах сплайна (при  ) функция
) функция  удовлетворяет граничным условиям, которые заключаются в непрерывности самой функции
удовлетворяет граничным условиям, которые заключаются в непрерывности самой функции  , а также ее первой
, а также ее первой  и второй
и второй  производных. Коэффициенты многочленов
производных. Коэффициенты многочленов  ,
,  ,
,  и
и  находятся из условия минимума функционала
находятся из условия минимума функционала
 (3.1)
(3.1)
где  - параметр сглаживания,
- параметр сглаживания,  - среднее значение сглаживаемой величины на периоде
- среднее значение сглаживаемой величины на периоде  ,
,  - среднее квадратическое отклонение сглаживаемой величины на периоде
- среднее квадратическое отклонение сглаживаемой величины на периоде  , а
, а  - значение сглаживающего сплайна на периоде
- значение сглаживающего сплайна на периоде  . Величина
. Величина

является взвешенной невязкой экспериментальных данных и сплайна, а величина
 Рис. 2. Подбор оптимального параметра сглаживания.
Рис. 2. Подбор оптимального параметра сглаживания.
|

определяет гладкость искомого сплайна.
Таким образом, при минимизации (3.1) получается решение, в некоторой степени удовлетворяющее двум противоречащим требованиям:
a) максимальной гладкости
b) минимальной невязке сплайна и экспериментальных данных.
Критерием, определяющим то, какому из требований отдается предпочтение, является точность экспериментальных данных. Чем ниже точность, тем более гладким должен быть сплайн. Технически соотношение между этими требованиями определяет параметр  , изменяющийся от 0 до 1 и играющий роль параметра регуляризации (рис. 2). При
, изменяющийся от 0 до 1 и играющий роль параметра регуляризации (рис. 2). При  априорная информация о гладкости кривой не учитывается и аппроксимирующая кривая проходит по средним значениям экспериментальных данных. При уменьшении
априорная информация о гладкости кривой не учитывается и аппроксимирующая кривая проходит по средним значениям экспериментальных данных. При уменьшении  гладкость кривой возрастает, но начинает увеличиваться невязка сплайна и экспериментальных данных. При
гладкость кривой возрастает, но начинает увеличиваться невязка сплайна и экспериментальных данных. При  сплайн превращается в прямую.
сплайн превращается в прямую.
Выбирая оптимальное значение параметра  , лучше начать с его крайнего значения, например 1. Невязка исходной (экспериментальной) и сглаженной кривых составит при этом 0. Далее следует постепенно уменьшать
, лучше начать с его крайнего значения, например 1. Невязка исходной (экспериментальной) и сглаженной кривых составит при этом 0. Далее следует постепенно уменьшать  до тех пор, пока невязка исходной и сглаженной кривых не станет равна дисперсии исходных данных. Соответствующее этой ситуации значение
до тех пор, пока невязка исходной и сглаженной кривых не станет равна дисперсии исходных данных. Соответствующее этой ситуации значение  и будет оптимальным.
и будет оптимальным.






