В множественном регрессионном анализе исследуется зависимость математического ожидания одной случайной величины от значений множества неслучайных величин.
В этом анализе совокупность наблюдений выходной случайной величины y можно представить в виде:
Y = X*B + E,
где X - матрица n*k значений входных переменных
Y - вектор-столбец n значений выходной переменной 
, B - вектор-столбец k коэффициентов регрессии 
, E - вектор-столбец n значений приведенных к выходу возмущений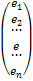 
.
ПРЕДПОСЫЛКИ РЕГРЕССИОННОГО АНАЛИЗА:
1. В каждом наблюдении ei имеет нормальное распределение с нулевым МО и конечной дисперсией.
2. Для любого i дисперсия ei является величиной постоянной.
3. Для любого i не равного j COV(ei,ej)=0. Это в соответствии с пунктом 1 означает, что ei и ej должны быть независимыми случайными величинами.
Решение системы нормальных уравнений доставляющее оценки коэффициентов множественной регрессии имеет вид:
Bоц = (Xт* X)-1*Xт*Y,
где Bоц - вектор-столбец МНК-оценок коэффициентов множественной регрессии
Xт - транспонированная матрица X;
(Xт*X)-1 - матрица обратная матрице Xт* X.
Несмещенной оценкой дисперсии возмущений является величина:
S2e = (Y - X*Bоц)т*(Y - X*Bоц)/(n - k),
где k - число оцениваемых коэффициентов в уравнении регрессии.
ПОЛУЧИВ МНК-ОЦЕНКИ Bоц КОЭФФИЦИЕНТОВ УРАВНЕНИЯ РЕГРЕССИИ НЕОБХОДИМО ПРОВЕРИТЬ ДЛЯ КАЖДОЙ ОЦЕНКИ ГИПОТЕЗУ О РАВЕНСТВЕ НУЛЮ ИСТИННОГО ЗНАЧЕНИЯ: Ho:bj=0.
Проверка гипотезы осуществляется сравнением вычисленной T-статистики с критическим значением при заданном уровне значимости и числе степеней свободы(ЧСС) N-k:
Tj = |bj|*[n*(1 - R2j0)]1/2/Se
где Rj0 - коэффициент множественной корреляции j-той входной переменной с остальными.
Если Tj>Tкр, то данные противоречат гипотезе о равенстве нулю истинного значения коэффициента bj (КОЭФФИЦИЕНТ ЗНАЧИМ), если нет, то bj следует считать нулевым (КОЭФФИЦИЕНТ НЕЗНАЧИМ).
По результатам проверки гипотез о равенстве нулю истинных значений коэффициентов множественной регрессии, составляющие с незначимыми коэффициентами должны быть исключены из модели. При этом, в общем случае оценки коэффициентов, оставшиеся в модели должны быть пересчитаны! Это обусловлено коррелированностью входных переменных (матрица Xт*X - недиагональна). Только в случае отсутствия взаимной корреляции входных переменных (матрица Xт*X - диагональна) нет необходимости вновь вычислять оценки коэффициентов регрессии.
Модели авторегрессии.
Достаточно часто на практике встречаются стационарные процессы, каждое настоящее значение Yt которых определяется предыдущими, накопленными ранее значениями Yt-1, Yt-2 и т.д. То есть, имеет место взаимосвязь или корреляция между этими значениями. А поскольку коррелируют друг с другом значения одного и того же ряда, такое явление называют автокорреляция.
Для того чтобы определить насколько процесс является автокоррелированным, осуществляют расчет коэффициентов парной корреляции между значениями этого ряда и ими же, сдвинутыми на некоторый шаг назад. Такие коэффициенты называются автокорреляционными. Для их вычисления в формулу расчета коэффициента парной корреляции последовательно подставляют попарно сравниваемые значения показателя Y в момент t и показатели этого же процесса Y, но сдвинутые во времени на некоторый шаг τ, то есть Yt-τ:
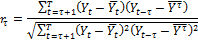
Где 
, и 
.
Таким образом, в качестве двух случайных переменных, между которыми выявляется корреляция, выступают исходный ряд значений Yt и ряд Yt-τ. Сам шаг τ изменяется от единицы до некоторого значения τМ. Поэтому в распоряжении прогнозиста находится некоторая зависимость коэффициента парной корреляции r от шага τ: r=f(τ). Эту зависимость называют автокорреляционной функцией. Наиболее наглядно свойства автокорреляции исходного ряда выявляются из графического анализа автокорреляционной функции. График зависимости значений коэффициента автокорреляции rτ от шага τ называют коррелограммой.
Анализ этого графика дает прогнозисту очень много ценной информации для выявления особенностей изучаемого процесса - периодичности некоторых явлений, их цикличности и сезонности, структура этой цикличности и т.п. Очевидно, что максимальные значения автокорреляционной функции могут изменяться в пределах от минус единицы до плюс единицы, а максимальное число сдвигов τМ не должно быть близким к числу наблюдений показателей τМ < Т.
Типичный график автокорреляционной функции:
Для большей наглядности на график коррелограммы наносят не только значения коэффициентов автокорреляции при соответствующих сдвигах τ, но ещё и соединяют близлежащие точки отрезками прямых линий. В результате получается некоторая ломаная линия, максимумы и минимумы которой и являются предметом особого изучения, ведь они характеризуют приближение зависимости между значениями ряда Yt и предыдущими значениями Yt-τ к линейной, причём, чем ближе величина коэффициента автокорреляции при каком-то шаге τ к 1, тем ближе к линейной зависимость между указанными значениями.
Если при некотором сдвиге τ коэффициент автокорреляции по модулю окажется не менее чем 0,8, то говорят о наличии этой зависимости, а сдвиг во времени τ, соответствующий этому высокому значению коэффициента, называют лагом. Если автокорреляционная функция имеет несколько лагов, то говорят о том, что у этого ряда имеются распределённые лаги. Впрочем, иногда о распределённых лагах говорят, если показатель yt находят в зависимости от другого фактора xt. Поскольку лаг означает наличие зависимости значений самого ряда от его же значений, но сдвинутых на величину лага, то эту зависимость можно описать математически. В общем случае модель авторегрессии может описываться следующей формулой: 
Применительно к графику автокорреляционной функции, на котором выделяются два лага, равные 5 и 7 соответственно, можно говорить о том, что модель авторегрессии будет содержать две переменные - Yt-5 и Yt-7. Поскольку при лаге, равном пяти, коэффициент автокорреляции имеет положительный знак, то коэффициент при переменной Yt-5 будет положительным, а так как коэффициент автокорреляции при лаге, равном семи, имеет отрицательный знак, что свидетельствует об обратной линейной зависимости, то и коэффициент при переменной Yt-7 будет отрицательным: 
.
Для нахождения коэффициентов модели авторегрессии используются соответствующие разделы математической статистики, в большинстве случаев для этого используется МНК.
