Побудова|шикування| і аналіз моделі множинної |численний| лінійної регресії

 

Мета|ціль| завдання|задавання| - вивчити основні підходи до аналізу і побудови|шикування| моделі множинної|численної| лінійної регресії, навчитися застосовувати їх при побудові|шикуванні| моделей реальних процесів.

 

2.1 Основні положення|становища|

Розглянемо|розгледимо| загальну|спільну| лінійну модель із|із| 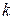змінними. Нехай 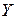|нехай| - залежна змінна, 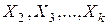- 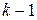незалежних змінних, 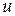- обурення|збурення| або випадкові помилки, 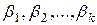- коефіцієнти або параметри моделі. Якщо одержані|отримані| вибірки із|із| спостережень над залежними і незалежними змінними, то загальну|спільну| лінійну модель можна записати в наступному|слідуючому| вигляді|виді|:

, .

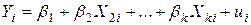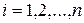Коефіцієнти 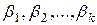і параметри розподілу 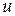невідомі. Потрібно отримати|отримати| оцінки параметрів 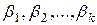і оцінки параметрів розподілу .

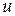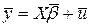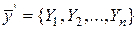Загальна|спільна| лінійна модель в матричній формі може бути записана в наступному|слідуючому| вигляді|виді|: , де - вектор залежних змінних; 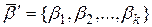- вектор невідомих параметрів моделі; 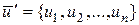- вектор випадкових обурень|збурень|;

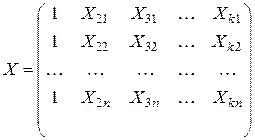- матриця спостережень.

Щодо|відносно| загальної|спільної| лінійної моделі, введені|запроваджені| наступні|слідуючі| передумови:

1.Випадкові обурення|збурення| мають нормальний закон розподілу з|із| нульовими математичними сподіваннями|чеканнями|, постійною дисперсією і статистично незалежні: ; .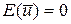

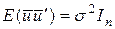2. Матриця 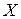утворена з|із| фіксованих чисел.

3.Ранг матриці рівний : .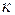

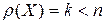Згідно методу найменших квадратів, для отримання|здобуття| вектора оцінок параметрів загальної|спільної| лінійної моделі 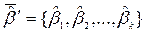використовується наступна|слідуюча| формула:

.

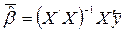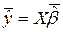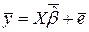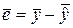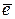Тоді можна записати, що , , , де - вектор -столбец залишків .

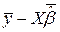Коваріаційна| матриця оцінок параметрів визначається таким чином:

.

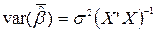Таким чином, дисперсію оцінки можна отримати|отримати|, помноживши 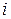-й елемент головної діагоналі матриці на дисперсію випадкового обурення|збурення|, а коваріацію| пари оцінок 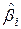и 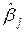можна| знайти множенням на елементу матриці з|із| індексом .

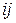Оцінка дисперсії випадкової помилки|бентежачої| дії визначається таким чином:

.

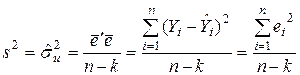Оцінка дисперсії 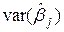оцінки параметра 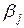визначається за формулою: 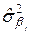= 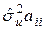, де 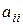- діагональний елемент матриці .
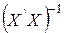Тоді середнє квадратичне відхилення параметра 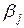прийме вигляд|вид|: = .

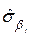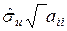Коефіцієнт детермінації R² обчислюється за формулою

.

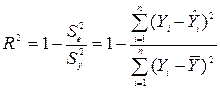Коефіцієнт детермінації R² з урахуванням|з врахуванням| поправки на число ступенів свободи визначається таким чином:

.

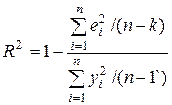Коефіцієнт множинної|численної| кореляції R є|з'являється,являється| коренем квадратним з|із| відповідного коефіцієнта детермінації: .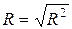

Перевіримо гіпотези про значущість кожного з параметрів моделі і побудуємо|спорудимо| для них довірчі інтервали.

Перевірятимемо нульову гіпотезу 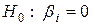при конкуруючій гіпотезі 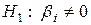. Фактично перевіряється гіпотеза про відсутності лінійного зв'язку між змінними 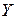і .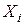

Критерій перевірки визначається за наступною|слідуючій| формулою:

= = ,

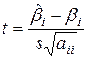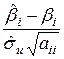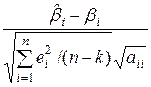де 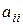- -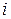й діагональний елемент матриці 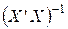. Даний критерій має -

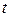розподіл Стьюдента з|із| 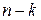ступенями свободи.

Значення критерію, що спостерігається, визначається за формулою:

= = .

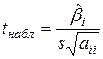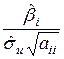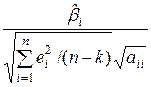Критичне значення критерію шукається по таблиці критичних точок розподілу Стьюдента для двосторонньої|двобічної| критичної області при рівні значущості 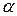і числі ступенів свободи : .

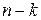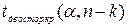Якщо 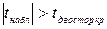, то нульова гіпотеза 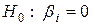відхиляється. Інакше робиться|чиниться| висновок|виведення| про статистичну незначущість параметра, тобто, відповідна незалежна змінна не впливає істотно|суттєво| на зміну залежної змінної в загальній|спільній| лінійній моделі.

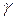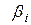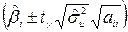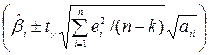Довірчі інтервали з надійністю для кожного окремого параметра задаються таким чином: або , де , .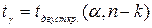

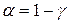Здійснимо сумісну|спільну| перевірку гіпотези щодо|відносно| значущості параметрів моделі 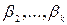. Розглядається|розглядується| нульова гіпотеза 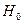про рівність нулю параметрів регресійної моделі: 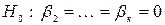. Дана гіпотеза дозволяє перевірити все співвідношення в цілому|загалом|, тобто встановити наявність зв'язку між незалежними змінними і залежною змінною .

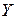Критерій перевірки має наступний|слідуючий| вигляд|вид|:

,

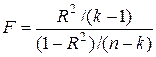має розподіл F-Фішера з|із| числом ступенів свободи 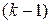і .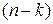

Значення критерію, що спостерігається, визначається відповідно до наступної|слідуючої| формули:

.

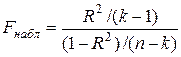Цей результат підводить базу під дисперсійний аналіз.

Критичне значення критерію вибирається по таблиці критичних точок Фішера по рівню значущості 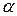і числу ступенів свободи 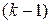і : .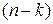

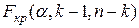Якщо 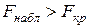, то нульова гіпотеза 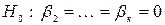відкидається при заданому рівні значущості 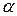. Відхилення нульової гіпотези свідчить про адекватність побудованої|спорудженої| моделі. Інакше модель вважається|лічиться| неадекватною.

 

2.2 Приклад|зразок|

Визначити вплив вказаних показників (виробництво товарів народного споживання|вжитку|, обсягу|обсяги| імпорту товарів, середньомісячна заробітна платня|плата|) на роздрібний товарообіг.

Побудувати|спорудити| модель множинної|численної| лінійної регресії, отримати|отримати| оцінки параметрів моделі по методу найменших квадратів, досліджувати статистичні властивості отриманих|отриманих| оцінок параметрів моделі.

Перевірити гіпотези про значущість кожного з параметрів моделі, побудувати|спорудити| для них довірчі інтервали.

Одержати|отримати| оцінку коефіцієнта детермінації і зробити попередній висновок|виведення| про ступінь|міру| тісноти зв'язку між змінними.

Перевірити значущість моделі за допомогою критерію Фішера.

Початкові|вихідні| дані приведені в табл|. 2.1.

 

Таблиця 2.1. Початкові|вихідні| дані

	Регіон	Виробництво товарів	Об'єми|обсяги| імпорту	Середньомісячна зарплата	Роздрібний товарообіг
№		X1	X2	X3	Y
	Крим	0,18	0,19	0,17	0,140
	Вінницька	0,54	0,35	0,45	0,340
	Волинська	0,45	0,23	0,47	0,330
	Дніпропетровська	0,87	0,81	0,77	0,650
	Донецька	4,49	4,19	4,81	6,160
	Жітомерськая	0,84	1,91	1,21	2,320
	Закарпатська	2,36	4,84	2,23	5,170
	Запорізька	0,45	0,83	0,69	2,110
	Івано-Франковс.	0,81	0,8	0,83	0,860
	Київська	0,46	0,66	0,55	0,790
	Кіровоградська	1,08	1,11	1,04	1,730
	Луганська	0,39	0,67	0,53	1,370
	Львівська	0,18	0,19	0,17	0,140
	Миколаївська	0,54	0,35	0,45	0,340
	Одеська	0,46	0,23	0,47	0,330
	Полтавська	0,87	0,81	0,77	0,650
	Рівненська	0,71	0,9	0,88	0,910
	Сумська	0,07	0,13	0,27	0,190
	Тернопільська	0,14	0,24	0,25	0,320
	Харківська	0,03	0,05	0,07	0,100
	Херсонська	0,136	0,176	0,154	0,129
	Хмельницька	0,073	0,064	0,182	0,088
	Черкаська	0,105	0,066	0,178	0,140
	Чернівецька	0,15	0,182	0,181	0,151
	Чернігівська	0,189	0,359	0,354	0,172

 

Рішення|розв'язання,вирішення,розв'язування|.

За приведеними даними модель множинної|численної| лінійної регресії має наступний|слідуючий| вигляд|вид|: 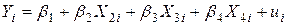, 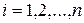. Тут 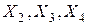- незалежні змінні ( 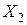- об'єм|обсяг| виробництва товарів народного споживання|вжитку|; 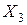- об'єм|обсяг| імпорту товарів; 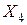-среднемесячная заробітна платня|плата|); 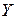- залежна змінна (роздрібний товарообіг); 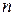-объем вибірки ( 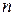=25).

Одержимо|отримаємо| оцінки параметрів загальної|спільної| лінійної моделі 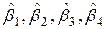і оцінку моделі множинної|численної| лінійної регресії .

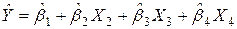Згідно методу найменших квадратів (МНК|), вектор оцінок параметрів моделі множинної|численної| лінійної регресії визначається таким чином: .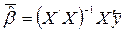

Всі проміжні розрахунки зведені в таблицю 2.2.

 

 

Таблиця 2.2. Приклад|зразок| розрахунку.

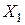
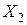
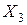
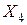
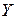
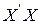
	0,18	0,19	0,17	0,14		25,00	16,57	20,34	18,13
	0,54	0,35	0,45	0,34		16,57	32,02	37,50	33,58
	0,45	0,23	0,47	0,33		20,34	37,50	50,90	39,31
	0,87	0,81	0,77	0,65		18,13	33,58	39,31	35,65
	4,49	4,19	4,81	6,16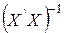
	0,84	1,91	1,21	2,32
	2,36	4,84	2,23	5,17		0,067	0,098	-0,009	-0,116
	0,45	0,83	0,69	2,11		0,098	2,932	-0,189	-2,603
	0,81	0,8	0,83	0,86		-0,009	-0,189	0,145	0,023
	0,46	0,66	0,55	0,79		-0,116	-2,603	0,023	2,513
	1,08	1,11	1,04	1,73
	0,39	0,67	0,53	1,37
	0,18	0,19	0,17	0,14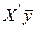
	0,54	0,35	0,45	0,34				25,63
	0,46	0,23	0,47	0,33				48,87
	0,87	0,81	0,77	0,65				63,61
	0,71	0,9	0,88	0,91				51,85
	0,07	0,13	0,27	0,19
	0,14	0,24	0,25	0,32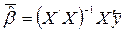
	0,03	0,05	0,07	0,1
	0,136	0,176	0,154	0,129		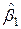		-0,105
	0,073	0,064	0,182	0,088		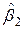		-1,192
	0,105	0,066	0,178	0,14		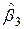		0,933
	0,15	0,182	0,181	0,151		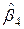		1,602
	0,189	0,359	0,354	0,172

 

Таким чином, оцінка моделі множинної|численної| лінійної регресії має наступний|слідуючий| вигляд|вид|: .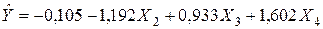

Одержимо|отримаємо| оцінку дисперсії випадкової помилки|бентежачої| 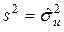і оцінки дисперсії 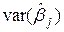оцінки параметра :

= = ;

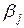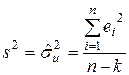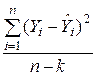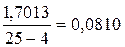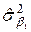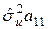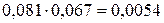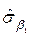= = ; =0,0735;

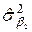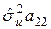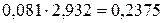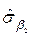= = ; =0,4874;

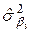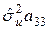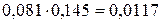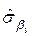= = ; =0,1083;

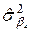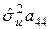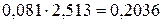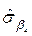= = ; =0,4512.

Перевіримо гіпотези про значущість кожного з параметрів моделі 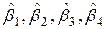. Перевірятимемо наступні|такі| нульові гіпотези 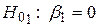, , 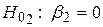, 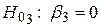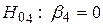при відповідних конкуруючих гіпотезах , , , .

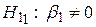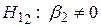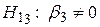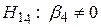Спостережувані значення критерію для кожної з гіпотез, що перевіряються, будуть рівні:

= = ; = = ;

= = ; = = .

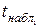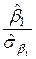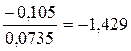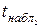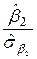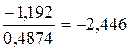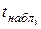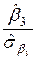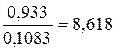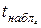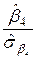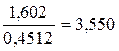Критичне значення критерію знайдемо по таблиці критичних точок розподілу Стьюдента для двосторонньої|двобічної| критичної області при рівні значущості 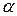=0,05 і числі ступенів свободи 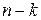=25-4=21: 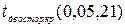=2,080.

Набутого спостережуваного значення критеріїв порівнюється з|із| критичним значенням критерію: 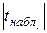< 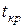, 1,429<2,080, тобто гіпотеза про значущість параметра 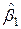приймається, таким чином, набутого значення параметра 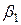статистично неістотно|несуттєво|; 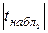> 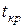, 2,446>2,080, тобто гіпотеза про значущість параметра 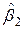відкидається, таким чином внесок|вклад| від включення|приєднання| змінної в модель володіє високою значущістю; 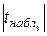> 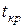, 8,618>2,080, тобто гіпотеза про значущість параметра 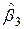відкидається, таким чином внесок|вклад| від включення|приєднання| змінної в модель володіє високою значущістю; 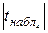> 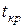, 3,550>2,080, тобто гіпотеза про значущість параметра 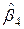відкидається, таким чином, внесок|вклад| від включення|приєднання| змінної в модель володіє високою значущістю.

Таким чином, можна розглядати|розглядувати| регресійну модель наступного|слідуючого| вигляду|виду|: .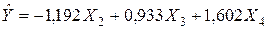

Довірчі інтервали для кожного окремого параметра 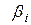задаються формулою 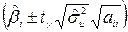і рівні: (); (); (); ().

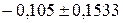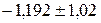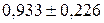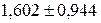Визначимо коефіцієнт детермінації:

= .

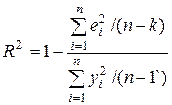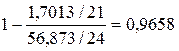Оскільки значення 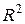близько|поблизу| до одиниці, то дану модель можна використовувати для аналізу і прогнозу економічних явищ.

Здійснимо сумісну|спільну| перевірку гіпотези щодо|відносно| значущості параметрів моделі 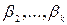. Розглядається|розглядується| нульова гіпотеза 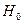про рівність нулю параметрів регресійної моделі: .

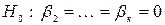Знайдемо значення критерію, що спостерігається, 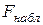таким чином:

= .

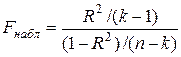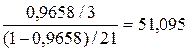Критичне значення критерію вибирається по таблиці критичних точок Фішера по рівню значущості 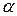і числу ступенів свободи 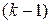і 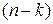: 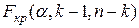. Одержимо|отримаємо| 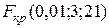=3,07.

Одержано|отримано|, що 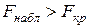, тому нульова гіпотеза 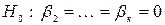відкидається при заданому рівні значущості 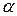. Відхилення нульової гіпотези свідчить про адекватність побудованої|спорудженої| моделі. Значущість зв'язку між змінними виявляється|опиняється| високою.

 

2.3 Завдання|задавання| для самостійної роботи

Вивчити основні етапи побудови|шикування| і аналізу моделі множинної|численної| лінійної регресії.

Відповісти на контрольні питання.

Виписати розрахункові формули для обчислення|підрахунку| оцінок параметрів моделі, дисперсій оцінок параметрів моделі, оцінки дисперсії випадкового обурення|збурення|, коефіцієнта детермінації.

Вивчити, як перевіряються гіпотези про значущість параметрів моделі множинної|численної| лінійної регресії і будуються для них довірчі інтервали.

Вивчити, як перевіряється гіпотеза про наявність лінійного зв'язку між змінними моделі в цілому|загалом|, зробити висновок|виведення| про адекватність моделі.

Сформувати вибірку залежних змінних 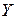відповідно до рівняння множинної|численної| лінійної регресії, використовуючи задані значення параметрів 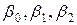і значення незалежних змінних X₁={1; 1,3; 2,5; 4,3; 4,8;} і X₂={ 5,3; 5,5; 6,3; 7,2;8}. Випадкових помилок використовувати як нормально розподілені випадкові величини з|із| нульовим математичним сподіванням|чеканням| і одиничною|поодинокою| дисперсією. Варіанти завдань|задавань| представлені|уявлені| в таблиці 2.3, а значення випадкових помилок представлені|уявлені| в таблиці 2.4.

 

 

Таблиця 2.3 Варіанти завдань|задавань|

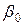
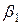
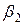
N				N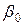
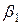
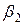
		-2
	-1,5	1,3			1,5		-2
	-2				-1		-2
	-1		-1,5		-1		-3
			-2		-2		-3
		-2			-2
	-3		0,5		-3
	-2,5		1,5		-1		1,5
					0,5		-1
					0,5		-2
					0,5
					0,9
							-2
							-3

 

Таблиця 2.4 Нормально розподілені випадкові числа

 

1,47	-1,79	2,27	-0,55	-0,38	-0,31	-0,52	-0,96	0,92
1,02	-1,79	2,27	-0,55	-0,38	-0,31	-0,52	-0,96	0,92
1,39	-0,10	0,04	-0,51	1,83	-2,10	0,01	0,73	-1,47
0,91	-1,34	-1,13	-1,05	0,53	0,08	-0,16	0,72	-0,85
0,18	1,04	0,77	-0,49	-2,06	-1,66	-1,62	-1,63	0,21
-1,50	0,28	0,37	0,70	-2,01	-0,34	0,38	1,11	1,27
-0,69	-1,80	-0,51	0,22	1,18	-0,52	-0,06	1,15	-0,57
1,37	-1,19	0,29	1,68	-1,14	2,99	1,36	-1,94	-0,32
-0,48	0,66	1,03	-0,15	0,36	2,45	-0,92	0,38	-0,19
-1,38	-0,44	0,14	0,60	-0,23	-0,53	0,01	-1,08	0,70

 

Одержати|отримати| ковариационную| матрицю оцінок параметрів .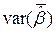

Побудувати|спорудити| довірчі інтервали для оцінок параметрів .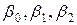

Перевірити гіпотези про значущість всіх коефіцієнтів регресії в цілому|загалом| і кожного окремо|нарізно|.

 

2.4 Контрольні питання і завдання|задавання|

1) Дати визначення моделі множинної|численної| лінійної регресії.

2) При яких основних припущеннях|гадках| досліджується модель множинної|численної| лінійної регресії?

3) Як обчислюються|обчисляються,вичисляють| оцінки параметрів моделі множинної|численної| лінійної регресії?

4) Які основні властивості оцінок параметрів у разі|в разі| моделі множинної|численної| лінійної регресії?

5) Як визначаються коефіцієнти множинної|численної| кореляції і детерміації в моделі множинної|численної| лінійної регресії?

6) Як побудувати|спорудити| довірчі інтервали параметрів множинної|численної| лінійної регресії?

7) Як перевіряються гіпотези про значущість параметрів множинної|численної| лінійної регресії?

8) Як перевіряється гіпотеза про наявність лінійного зв'язку між змінними в цілому|загалом|?

ДОДАТОК Б

Таблиця Б.1 - Критичні точки розподілу Стьюдента

Число ступенів свободи	Рівень значимості (двостороння критична область)
k	0.10	0.05	0.02	0.01	0. 002	0. 001
	6.31	12.7	31.82	63.7	318.3	637.0
	2.92	4.30	6.97	9.92	22.33	31.6
	2.35	3.18	4.54	5.84	10.22	12.9
	2.13	2.78	3.75	4.60	7.17	8.61
	2.01	2.57	3.37	4.03	5.89	6.86
	1.94	2.45	3.14	3.71	5.21	5.96
	1.89	2.36	3.00	3.50	4.79	5.40
	1.86	2.31	2.90	3.36	4.50	5.04
	1.83	2.26	2.82	3.25	4.30	4.78
	1.81	2.23	2.76	3.17	4.14	4.59
	1.80	2.20	2.72	3.11	4.03	4.44
	1.78	2.18	2.68	3.05	3.93	4.32
	1.77	2.16	2.65	3.01	3.85	4.22
	1.76	2.14	2.62	2.98	3.79	4.14
	1.75	2.13	2.60	2.95	3.73	4.07
	1.75	2.12	2.58	2.92	3.69	4.01
	1.74	2.11	2.57	2.90	3.65	3.96
	1.73	2.10	2.55	2.88	3.61	3.92
	1.73	2.09	2.54	2.86	3.38	3.88
	1.73	2.09	2.53	2.85	3.55	3.85
	1.72	2.08	2.52	2.83	3.53	3.82

 

Продовження табл.Б.1

	1.72	2.07	2.51	2.82	3.51	3.79
	1.71	2.07	2.50	2.81	3.49	3.77
	1.71	2.06	2.49	2.80	3.47	3.74
	1.71	2.06	2.49	2.79	3.45	3.72
	1.71	2.06	2.48	2.78	3.44	3.71
	1.71	2.05	2.47	2.77	3.42	3.69
	1.70	2.05	2.46	2.76	3.40	3.66
	1.70	2.05	2.46	2.76	3.40	3.66
	1.70	2.04	2.46	2.75	3.39	3.65
	1.68	2.02	2.42	2.70	3.31	3.55
	1.67	2.00	2.39	2.66	3.23	3.46
	1.66	1.98	2.36	2.62	3.17	3.37
k	0.05	0. 025	0.01	0. 005	0. 001	0. 0005
Число ступенів свободи	Рівень значимості (одностороння критична область)

 

Таблиця Б.2 - Квантилі розподілу Фішера

k	l
									¥
	161.40	199.50	215.70	224.60	230.20	234.00	238.90	243.90	249.00	254.30
	18.51	19.00	19.16	19.25	19.30	19.33	19.37	19.41	19.45	19.50
	10.13	9.55	9.28	9.12	9.01	8.94	8.84	8.74	8.64	8.53
	7.71	6.94	6.59	6.39	6.26	6.16	6.04	5.91	5.77	5.63
	6.61	5.79	5.41	5.19	5.05	4.95	4.82	4.68	4.53	4.36
	5.99	5.14	4.76	4.53	4.39	4.28	4.15	4.00	3.84	3.67
	5.59	4.74	4.35	4.12	3.97	3.87	3.73	3.57	3.41	3.23

 

Продовження табл. Б.2

	5.32	4.46	4.07	3.84	3.69	3.58	3.44	3.28	3.12	2.93
	5.12	4.26	3.86	3.63	3.48	3.37	3.23	3.07	2.90	2.71
	4.96	4.10	3.71	3.48	3.33	3.22	3.07	2.91	2.74	2.54
	4.84	3.68	3.59	3.36	3.20	3.09	2.95	2.79	2.61	2.40
	4.75	3.88	3.49	3.26	3.11	3.00	2.85	2.69	2.50	2.30
	4.67	3.80	3.41	3.18	3.02	2.92	2.77	2.60	2.42	2.21
	4.60	3.74	3.34	3.11	2.96	2.85	2.70	2.53	2.35	2.13
	4.54	3.68	3.29	3.06	2.90	2.79	2.64	2.48	2.29	2.07
	4.49	3.63	3.24	3.01	2.85	2.74	2.59	2.42	2.24	2.01
	4.45	3.59	3.20	2.96	2.81	2.70	2.55	2.38	2.19	1.96
	4.41	3.55	3.16	2.93	2.77	2.66	2.51	2.34	2.15	1.92
	4.33	3.52	3.13	2.90	2.74	2.63	2.48	2.31	2.11	1.88
	4.35	3.49	3.10	2.87	2.71	2.60	2.45	2.28	2.08	1.84
	4.32	3.47	3.07	2.84	2.68	2.57	2.42	2.25	2.05	1.81
	4.30	3.44	3.05	2.82	2.66	2.55	2.40	2.23	2.03	1.78
	4.28	3.42	3.03	2.80	2.64	2.53	2.38	2.20	2.00	1.76
	4.26	3.40	3.01	2.78	2.62	2.51	2.36	2.18	1.98	1.73
	4.24	3.38	2.99	2.76	2.60	2.49	2.34	2.16	1.96	1.71
	4.22	3.37	2.98	2.74	2.59	2.47	2.32	2.15	1.95	1.69
	4.21	3.35	2.96	2.73	2.57	2.46	2.30	2.13	1.93	1.67
	4.20	3.34	2.95	2.71	2.56	2.44	2.29	2.12	1.91	1.65
	4.18	3.33	2.93	2.70	2.54	2.43	2.28	2.10	1.90	1.64
	4.17	3.32	2.92	2.69	2.53	2.42	2.27	2.09	1.89	1.62
	4.08	3.23	2.84	2.61	2.45	2.34	2.18	2.00	1.79	1.51
	4.00	3.15	2.76	2.52	2.37	2.25	2.10	1.92	1.70	1.39
	3.92	3.07	2.68	2.45	2.29	2.17	2.02	1.83	1.61	1.25
¥	3.84	2.99	2.60		2.21	2.09	1.94	1.75	1.52	1.00