Примеры выполнения заданий

МОДУЛЬ 2. ЧИСЛЕННЫЕ МЕТОДЫ

 

Лабораторная работа № 1

ПРИБЛИЖЕННОЕ РЕШЕНИЕ АЛГЕБРАИЧЕСКИХ

И ТРАНСЦЕНДЕНТНЫХ УРАВНЕНИЙ

МЕТОДОМ ПОЛОВИННОГО ДЕЛЕНИЯ (ДИХОТОМИИ)

 

Цель работы: используя метод половинного деления, вычислить с точностью до все действительные корни полинома .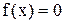

 

Постановка задачи

1. Отделить корни для заданного алгебраического уравнения 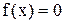.Для решения этой задачи можно использовать аналитический, графический или табличный метод.

2. Уточнить один из корней методом дихотомии (ручной счет, 5-7 итераций).

3. Решить задачу уточнения корней двумя способами в пакете МathCAD, используя оператор if и программный блок.

4. Решить задачу отделения и уточнения корней методом половинного деления в среде MATLAB.

5. Сравнить все полученные результаты. Проверить правильность результатов с помощью встроенных функций пакетов. Сделать выводы.

 

Теоретические сведения

Постановка задачи. Решение уравнений является одной из задач, наиболее часто встречающихся в практике инженера. Всякое уравнение с одним неизвестным можно записать в виде

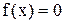. (1.1)

Решением уравнения (1.1) называется такое значение (корень уравнения), при котором . Формулы для нахождения точного значения корней известны только для узкого класса уравнений. На практике часто встречаются уравнения, которые невозможно решить с помощью элементарных приемов. Кроме того, в инженерных расчетах в большинстве случаев нельзя говорить о точном решении уравнений, так как входящие в них коэффициенты заданы приближенно. Поэтому важное значение приобретают методы, позволяющие сколь угодно точно находить корни уравнения (1.1).

Задача решения уравнения с заданной точностью обычно содержит два этапа:

а) отделение корней – выделение отрезков, в которых содержится один и только один корень уравнения (1.1);

б) уточнение приближенных корней, т.е. вычисление их с требуемой точностью.

Для каждого из этапов решения задачи разработаны свои численные методы.

Отделение действительных корней. Рассмотрим уравнение (1.1). Для отделения корней используем теорему Больцано–Коши: если непрерывная функция принимает значения разных знаков на концах отрезка , т.е. , то внутри этого
отрезка находится по крайней мере один корень уравнения 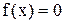. Этот корень будет единственным, если производная существует и сохраняет постоянный знак внутри интервала .
На практике часто используют табличный метод отделения корней и графический.

1. Табличный метод (метод перебора).

Находим знаки функции в ряде точек из области определения функции , , , …. Если 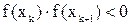, то в силу сформулированной выше теоремы на отрезке имеется по крайней мере один корень уравнения 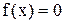. Теперь нужно тем или иным способом проверить, является ли этот корень единственным. Если на отрезке не меняет знак, корень – единственный (в силу монотонности ).

2. Графический метод.

Строим график функции и по чертежу находим интервалы, содержащие абциссы точек пересечения графика функции с осью , т.е. нули функции . Если уравнение не имеет близких по значению корней, то этим способом корни легко отделяются. Иногда уравнение 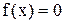удобно представить в виде 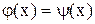, где функции – более простые, и, построив графики функций и , определить интервалы, содержащие точки их пересечения.

Рассмотрим этап отделения корней в случае алгебраического уравнения n-степени ():

, (1.2)

где коэффициенты – действительные числа, причем .

Основная теорема алгебры: алгебраическое уравнение n-степени (а следовательно, и полином P(x)) имеет ровно n корней, действительных или комплексных, при условии, что каждый корень считается столько раз, какова его кратность.

Теорема 1. Если коэффициенты алгебраического уравнения (1.2) действительные, то комплексные корни этого уравнения попарно комплексно-сопряженные, т.е. если ( – действительные) есть корень уравнения (1.2) кратности s, то число 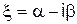также является корнем этого уравнения и имеет ту же кратность s.

Следствие. Алгебраическое уравнение нечетной степени с действительными коэффициентами имеет по меньшей мере одиндействительный корень.

Грубая оценка модулей корней уравнения (1.2) получается на основании теоремы 2.

Теорема 2. Пусть , где – коэффициенты уравнения (1.2). Тогда модули всех корней уравнения (1.2) удовлетворяют неравенству

,

т.е. корни этого уравнения на комплексной плоскости расположены внутри круга.

Уточнение корня методом половинного деления. Пусть найден отрезок , на котором находится единственный корень уравнения . Обозначим его . Для нахождения корня уравнения делим отрезок пополам. Если , то и задача решена. В случае выбираем ту половину отрезка , на концах которой функция имеет противоположные знаки. Новый суженный отрезок снова делим пополам, повторяем те же действия и т.д. В результате на каком-то этапе получаем точный корень уравнения или последовательность вложенных друг в друга отрезков , ,…, ,…. Доказано, что . Для вычисления корня уравнения с точностью до отрезок делим до тех пор, пока выполнится условие . За приближённое значение корня выбираем среднее значение на отрезке :

.

Дихотомия проста и надежна: к простому корню она сходится для любых непрерывных функций , в том числе и недифференцируемых. Метод половинного деления устойчив к погрешностям округления, но сходится он медленно. Количество итераций, необходимое для достижения заданной точности , можно оценить заранее по формуле

.

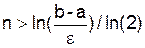Примеры выполнения заданий

Пример ручного счета

Вычислить с точностью действительный корень уравнения

.

Рассмотрим функцию 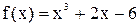.(требуемая форма уравнения должна быть f(x)=0).

Интервал изоляции корня [1;2], т.к. f(1)=-3 и f(2)=6.

Соответственно, корень заданного уравнения находится внутри интервал [1, 2] и является единственным, т.к. >0 для всех аргументов х.

Обозначим а₀=1, b₀=2. Процесс деления пополам нужно продолжать до тех пор, пока .

Вычисления оформим в виде табл. 1.1 (приведено 5 итераций).

Табл 1.1

	1.25 1.375 1.4375	1.5 1.5 1.5 1.5	0.5 0.25 0.125 0.0625	1.5 1.25 1.375 1.4375 1.46875	0.37 -1.58 -0.65 -0.15

 

Ответ: .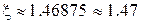

Заметим, что в данном примере оформления метода половинного деления нет необходимости вычисления f(x) в крайних точках интервала, т.к. заранее определено, что в точке a_n функция f(x) должна быть положительна, а в b_n - отрицательна. Точность метода определяется по значению модуля разности

Расчет в пакете MATHCAD

Пусть требуется вычислить корни уравнения

с точностью e =10^-5.

1. Интервалы изоляции корней для заданного уравнения определяются с помощью графика:

Интервалы изоляции корней:

 

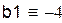
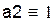
2. Решение уравнения методом половинного деления с использованием if:

 

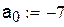
Замечание. Для увеличения точности необходимо увеличить количество итераций или необходимое количество итераций n можно задать с помощью формулы

 

 

3. Решение уравнения методом половинного деления с использованием простейшего программного блока:

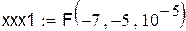
Программный блок с проверкой корректности задания отрезка, содержащего корень уравнения, и с подсчетом количества итераций для выполнения заданной точности решения может иметь такой вид:

4. Решение уравнения с помощью встроенных функций.

Решение уравнения с помощью встроенной функции root:

– переопределение встроенной точности решения

Решение уравнения с помощью функции polyroots:

 

 

Расчет в пакете MATLAB

1. Сравнение кодов метода дихотомии в пакетах MATHCAD и MATLAB представлено в виде табл.1.1.

Табл.1.1.

MATHCAD	MATLAB
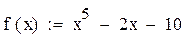
	function res = f(x) res=x^5-2*x-10 end
	function [rez, k] =R(a, b, eps) if f(a)*f(b)>0 error('error'); else i=0; while abs(b-a)>2* eps c=(a+b)/2; if f(c)*f(a)>0 a=c; end if f(c)*f(b)>0 b=c; end if f(c)==0 break; end i=i+1; end rez=c k=i end
	>> R(0,2,0.00000); rez = 1.6794 k =52

2. Функция отделения и уточнения корней для решения алгебраического уравнения .

function RTS=dixotomia(pol,eps);

% метод половинного деления для решения алгебраических уравнений

% функция определяет интервалы изоляции действительных корней

% формирует вектор действительных корней уравнения

% левая граница интервала, содержащего все корни уравнения

A0=-1-max(abs(pol))/(abs(pol(1)));

disp(A0)

% правая граница интервала, содержащего все корни уравнения

A1=-A0;

disp(A1)

d=A0;

d1=d;

i=1;

while d<=A1 % цикл отделения действительных корней (шаг 0.1)

d=d+0.1;

if polyval(pol,d)*polyval(pol,d1)<0

K(i)=d1;K(i+1)=d;

i=i+2;

end;

d1=d;

end;

disp(K);

% количество действительных корней

nrts=i-1;

i=1; j=1;

while i<nrts % цикл уточнения действительных корней

X=K(i); X1=K(i+1); x=X; x1=X1;

% метод половинного деления

while abs(polyval(pol,x)-polyval(pol,x1))>eps

x1=X; x=(X+X1)/2;

if polyval(pol,x)*polyval(pol,x1)>0

X=(X+X1)/2;

else

X1=(X+X1)/2;

end;

end;

% вектор, содержащий действительные корни уравнения

RTS(j)=x1; i=i+2; j=j+1;

end

RTS;

end

Результаты вычислений:

>> dixotomia([1 3 -12],0.00001) – вызов функции; полином задается значениями коэффициентов

-13 – левая граница интервала, содержащего корни уравнения

13 – правая граница интервала, содержащего корни уравнения

-5.3000 -5.2000 2.2000 2.3000 – интервалы изоляции корней

RTS =

-5.2749 2.2749 – корни уравнения

В арианты лабораторных работ

 

Номер варианта	Уравнение	Номер варианта	Уравнение
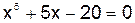
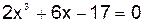
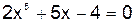