Определение 1. Элементарными преобразованиями матриц будем называть следующие преобразования:
1) умножение всех элементов какой-либо строки (столбца) на одно и то же число, отличное от нуля.
Обозначение для строк: 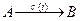 ,
, 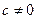 . Для столбцов:
. Для столбцов:  ,
, 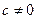 .
.
2) прибавление к элементам одной строки (столбца) соответствующих элементов другой строки (столбца), умноженных на одно и то же число;
Обозначение для строк:  . Для столбцов:
. Для столбцов: 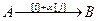 .
.
3) перемена местами двух строк (столбцов).
Обозначение для строк:  . Для столбцов:
. Для столбцов:  .
.
Если матрица  получена из матрицы
получена из матрицы  с помощью элементарных преобразований, то будем записывать это так:
с помощью элементарных преобразований, то будем записывать это так:  .
.
Лемма 1. Элементарные преобразования третьего типа равносильны нескольким последовательно выполненным преобразованиям первых двух типов.
Доказательство. Пусть матрица  получилась из матрицы
получилась из матрицы  в результате перемены местами
в результате перемены местами  - ой и
- ой и  - ой строки, т.е.
- ой строки, т.е.  . Покажем, что матрица
. Покажем, что матрица  может быть получена из матрицы
может быть получена из матрицы  в результате элементарных преобразований только первых двух типов.
в результате элементарных преобразований только первых двух типов.

 . Таким образом, получили матрицу
. Таким образом, получили матрицу  , что и требовалось доказать. Совершенно аналогично это утверждение доказывается для столбцов.
, что и требовалось доказать. Совершенно аналогично это утверждение доказывается для столбцов.
Лемма 2. Элементарные преобразования матриц обратимы, т.е. если  , то и
, то и 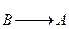 .
.
 Доказательство. Если матрица
Доказательство. Если матрица  получилась из матрицы
получилась из матрицы  в результате умножения всех элементов
в результате умножения всех элементов  - ой строки на число
- ой строки на число 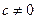 ,т.е.
,т.е. 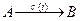 то и матрица
то и матрица  получается из матрицы
получается из матрицы  в результате умножения всех элементов
в результате умножения всех элементов  - ой строки на число
- ой строки на число  , т.е.
, т.е. 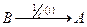 .
.
Если матрица  получилась из матрицы
получилась из матрицы  в результате прибавления к элементам
в результате прибавления к элементам  - ой строки матрицы
- ой строки матрицы  соответствующих элементов
соответствующих элементов  - ой строки, умноженных на число
- ой строки, умноженных на число  ,т.е.
,т.е.  то и матрица
то и матрица  получается из матрицы
получается из матрицы  в результате прибавления к элементам
в результате прибавления к элементам  - ой строки матрицы
- ой строки матрицы  соответствующих элементов
соответствующих элементов  - ой строки, умноженных на число
- ой строки, умноженных на число  , т.е.
, т.е.  .
.
Если матрица  получилась из матрицы
получилась из матрицы  в результате перемены местами
в результате перемены местами  - ой и
- ой и  - ой строки, т.е.
- ой строки, т.е.  , то матрица
, то матрица  также получается из матрицы
также получается из матрицы  результате перемены местами
результате перемены местами  - ой и
- ой и  - ой строки, т.е.
- ой строки, т.е. 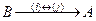 , и лемма 2 доказана. Совершенно аналогично это утверждение доказывается для столбцов.
, и лемма 2 доказана. Совершенно аналогично это утверждение доказывается для столбцов.
Лемма 3. Если  , то
, то  .
.
Доказательство проведём лишь для элементарных преобразований над строками, т.к. при транспонировании ранг матрицы не меняется. Пусть  . Мы хотим доказать, что
. Мы хотим доказать, что  . По следствию к лемме 2 §10 это будет доказано, если мы докажем, что все миноры (
. По следствию к лемме 2 §10 это будет доказано, если мы докажем, что все миноры ( )-го порядка матрицы
)-го порядка матрицы  равны 0. В силу леммы 1 это достаточно доказать лишь для случая, когда матрица
равны 0. В силу леммы 1 это достаточно доказать лишь для случая, когда матрица  получена из матрицы
получена из матрицы  с помощью элементарных преобразований 1-го и 2-го типа.
с помощью элементарных преобразований 1-го и 2-го типа.
1)Пусть матрица  получилась из матрицы
получилась из матрицы  в результате умножения всех элементов
в результате умножения всех элементов  - ой строки на число
- ой строки на число 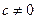
и пусть  - минор (
- минор ( )-го порядка матрицы
)-го порядка матрицы  . Могут представиться следующие случаи:
. Могут представиться следующие случаи:
а)  - ая строка не входит в состав минора
- ая строка не входит в состав минора  . Тогда
. Тогда  как минор (
как минор ( )-го порядка матрицы
)-го порядка матрицы  .
.
б)  - ая строка входит в состав минора
- ая строка входит в состав минора  . Тогда
. Тогда  , где
, где  - минор (
- минор ( )-го порядка матрицы
)-го порядка матрицы  , стоящий в строках и столбцах с теми же номерами, что и
, стоящий в строках и столбцах с теми же номерами, что и  . Здесь мы воспользовались свойством 5 определителей. Следовательно,
. Здесь мы воспользовались свойством 5 определителей. Следовательно,  как минор (
как минор ( )-го порядка матрицы
)-го порядка матрицы  , т.к.
, т.к.  . Отсюда получаем:
. Отсюда получаем:  .
.
2) Пусть матрица  получилась из матрицы
получилась из матрицы  в результате прибавления к элементам
в результате прибавления к элементам  - ой строки соответствующих элементов
- ой строки соответствующих элементов  - ой строки, умноженных на число
- ой строки, умноженных на число  , и пусть
, и пусть  - минор (
- минор ( )-го порядка матрицы
)-го порядка матрицы  . Могут представиться следующие случаи:
. Могут представиться следующие случаи:
а)  - ая строка не входит в состав минора
- ая строка не входит в состав минора  . Тогда
. Тогда  как минор (
как минор ( )-го порядка матрицы
)-го порядка матрицы  .
.
б) и  - ая, и
- ая, и  - ая строки входят в состав минора
- ая строки входят в состав минора  . Тогда:
. Тогда:
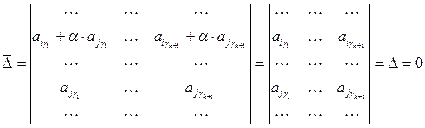 ,
,
т.к.  - минор (
- минор ( )-го порядка матрицы
)-го порядка матрицы  . Здесь мы воспользовались свойством 7 определителей.
. Здесь мы воспользовались свойством 7 определителей.
в)  - ая строка входит, а
- ая строка входит, а  - ая строка не входит в состав минора
- ая строка не входит в состав минора  . Тогда:
. Тогда:

Здесь мы воспользовались свойствами 6 и 5 определителей.
 - минор (
- минор ( )-го порядка матрицы
)-го порядка матрицы  . Определитель
. Определитель 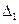 в общем случае не является минором (
в общем случае не является минором ( )-го порядка матрицы
)-го порядка матрицы  , т.к. выделенная строка может оказаться не на «своём» месте. Определитель
, т.к. выделенная строка может оказаться не на «своём» месте. Определитель 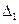 отличается от некоторого минора (
отличается от некоторого минора ( )-го порядка матрицы
)-го порядка матрицы  только порядком строк, и потому
только порядком строк, и потому  .
.
Лемма 3 доказана.
Проиллюстрируем на примере рассуждение пункта в) доказанной леммы 3.
Пример. Пусть матрица  получилась из матрицы
получилась из матрицы  в результате прибавления к элементам 1-ой строки соответствующих элементов 3-ей строки, умноженных на число 2:
в результате прибавления к элементам 1-ой строки соответствующих элементов 3-ей строки, умноженных на число 2:
 .
.
Рассмотрим  - минор 2-го порядка матрицы
- минор 2-го порядка матрицы  , стоящий в первых 2-х столбцах и в строках с номерами 1 и3
, стоящий в первых 2-х столбцах и в строках с номерами 1 и3

Определитель  не является минором матрицы
не является минором матрицы  , т.к. строки стоят в другом порядке, но определитель
, т.к. строки стоят в другом порядке, но определитель 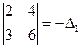 , отличающийся от предыдущего только порядком строк, является минором 2-го порядка матрицы
, отличающийся от предыдущего только порядком строк, является минором 2-го порядка матрицы  и потому равен 0, т.к.
и потому равен 0, т.к.  .
.
Теорема 1. В результате элементарных преобразований ранг матрицы не меняется, т.е. если  , то
, то
 .
.
Доказательство. Пусть  . Тогда по лемме3
. Тогда по лемме3  . Элементарные преобразования обратимы (по лемме 2). Следовательно, в этом случае матрица
. Элементарные преобразования обратимы (по лемме 2). Следовательно, в этом случае матрица  может быть получена из матрицы
может быть получена из матрицы  в результате элементарных преобразований, и по лемме 3 получаем:
в результате элементарных преобразований, и по лемме 3 получаем:  . Таким образом,
. Таким образом,  , и теорема доказана.
, и теорема доказана.
Теорема 2. Любая матрица с помощью элементарных преобразований над строками и, возможно, перестановки столбцов, может быть преобразована в трапециевидную.
Доказательство. Если матрица нулевая,то она трапециевидная по определению, и доказывать нечего.
Если она ненулевая, то она содержит ненулевой элемент, который с помощью перестановки строк и столбцов можно переместить в левый верхний угол. Поэтому будем считать, что  . Пусть матрица
. Пусть матрица  имеет следующий вид:
имеет следующий вид:
 .
.
Совершим следующие элементарные преобразования над строками:
 .
.
Если матрица  , то уже получили трапециевидную матрицу.
, то уже получили трапециевидную матрицу.
В противном случае с помощью перестановки последних 
 строк и последних
строк и последних  столбцов добьёмся того, чтобы элемент, стоящий во 2-ом столбце и во 2-ой строке был бы отличен от нуля. Поэтому будем считать, что
столбцов добьёмся того, чтобы элемент, стоящий во 2-ом столбце и во 2-ой строке был бы отличен от нуля. Поэтому будем считать, что  .
.
Теперь совершим следующие элементарные преобразования над строками:
 .
.
Если  , то получили трапециевидную матрицу.
, то получили трапециевидную матрицу.
В противном случае продолжим этот процесс до тех пор, пока в нескольких последних строках все элементы не будут равны 0, т.е.  , или пока не исчерпаем все строки. В результате получим трапециевидную матрицу.
, или пока не исчерпаем все строки. В результате получим трапециевидную матрицу.
Следствие. Любая матрица  строения
строения  ранга
ранга  с помощью элементарных преобразований над строками и, возможно, перестановки столбцов, может быть преобразована в матрицу вида:
с помощью элементарных преобразований над строками и, возможно, перестановки столбцов, может быть преобразована в матрицу вида:
 .
.
Если  , то последние нулевые строки отсутствуют. Если
, то последние нулевые строки отсутствуют. Если  , то эта матрица имеет вид:
, то эта матрица имеет вид:  .
.
Доказательство. Из доказанной теоремы следует, что матрица  с помощью указанных преобразований может быть преобразована в матрицу
с помощью указанных преобразований может быть преобразована в матрицу
 , причём
, причём  для всех
для всех  .
.
Совершим следующие элементарные преобразования над строками:
 .
.
Теперь с помощью  -ой строки получим в
-ой строки получим в  -ом столбце в строках с номерами
-ом столбце в строках с номерами  нули. Для этого от
нули. Для этого от
 -ой строки отнимем
-ой строки отнимем  -ю, умноженную на
-ю, умноженную на  (
(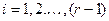 ).В результате получим матрицу:
).В результате получим матрицу:
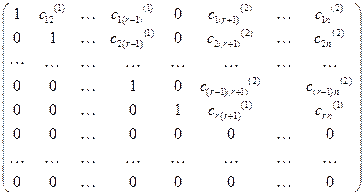 . Теперь действуя аналогично
. Теперь действуя аналогично  -ой строкой получим нули в
-ой строкой получим нули в  -ом столбце в строках с номерами
-ом столбце в строках с номерами  и т.д.
и т.д.
Замечание. Можно доказать, что если базисный минор матрицы  стоит в первых
стоит в первых  столбцах, то можно получить матрицы указанного вида совершая элементарные преобразования только над строками.
столбцах, то можно получить матрицы указанного вида совершая элементарные преобразования только над строками.
Покажем это на примере.
Пример.

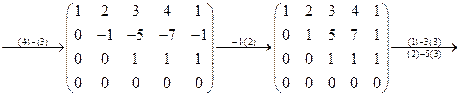

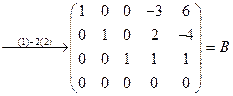 . Матрица
. Матрица  имеет такое же строение, как и матрица, рассмотренная в следствии. Здесь единичная матрица имеет порядок 3, т.к.
имеет такое же строение, как и матрица, рассмотренная в следствии. Здесь единичная матрица имеет порядок 3, т.к.  , роль матрицы
, роль матрицы  выполняет матрица, стоящая в последних двух столбцах и первых трёх строках матрицы
выполняет матрица, стоящая в последних двух столбцах и первых трёх строках матрицы  .
.






