Задание 1 Несимметричное шифрование – дешифрование.
Зашифровать информацию по методу RSA для последующей передачи. Вариант задания определяется последними цифрами номера студенческого билета. По номеру i (предпоследняя цифра) студент выбирает сообщение для зашифровывания, по j – требуемые для реализации этого алгоритма числа р и q.
Исходные данные:
| I | |||||
| Сообщение | Принтер | Интеграл | Минус | Модуль | Плюс |
| G | |||||
| p q | 7.11 | 5.17 | 3.11 | 11.19 | 13.17 |
| I | |||||
| Сообщение | Число | Дробь | Корень | Остаток | Степень |
| G | |||||
| p q | 7.17 | 5.11 | 7.13 | 11.17 | 5.13 |
Методические указания к решению задания 1
Одним из наиболее распространенных методов несимметричного шифрования- дешифрования является метод шифрования с открытым ключом, в котором используется алгоритм RSA.
Алгоритм основан на использовании операции возведения в степень модульной арифметики. Его можно представить в виде следующей последовательности шагов:
Шаг 1. Выбирается два больших простых числа числа р и q. Простыми называются числа, которые делятся на самих себя и на 1. На практике для обеспечения криптостойкости системы величина этих чисел должна быть длиной не менее двухсот десятичных разрядов.
Шаг 2. Вычисляется открытая компонента ключа n
n = р q.
Шаг 3. Находится функция Эйлера по формуле
f(р q.)=(р-1)(q-1)
Функция Эйлера показывает количество целых положительных чисел от1 до n, которые не имеют ни одного общего делителя, кроме 1.
Шаг 4. Выбирается число е, которое должно взаимно простым со значением функции Эйлера и меньшим, чем f(р q.)
Шаг 5. Определяется число d, удовлетворяющее соотношению
е * d(mod f(р q.))=1
Числа е и n принимаются в качестве открытого ключа. В качестве секретного ключа используются числа d и n.
Шаг 6. Исходная информация независимо от её физической природы представляется в числовом двоичном виде. Последовательность бит разделяется на блоки длиной L бит, где L – наименьшее целое число, удовлетворяющее условию
L ³ log2(n.+1); Каждый блок рассматривается как целое положительное число X(i), принадлежащее интервалу (0, n-1). Таким образом, исходная информация представляется последовательностью чисел X(i), (i = 1.I).Значение I определяется длиной шифруемой последовательности.
Шаг 7 Зашифрованная информация получается в виде последовательности чисел Y(i)= (Y(i)) e (mod n).
Шаг 8.Для расшифрования информации используется следующая зависимость
Х(i)= (Y(i)) e (mod n).
Рассмотрим числовой пример применения метод RSA для криптографического закрытия информации, в котором для простоты вычислений использованы минимально возможные числа. Пусть требуется зашифровать сообщение на русском языке ПРЕДЕЛ.
Сообщение: ПРЕДЕЛ
Простые числа p и q - 3,11
Зашифруем и расшифруем сообщение "ПРЕДЕЛ" по алгоритму RSA.
1) Выберем p=3 and q=11.
2)Вычислим открытую компоненту ключа: n= 3*11=33.
3) Определим функцию Эйлера: (p-1)*(q-1)=20. Следовательно, d будет равно, например, 3: (d=3).
4) Выберем число е по следующей формуле: (e*3) mod 20=1. е будет равно 7: (e=7).
Числа е и n принимаются в качестве открытого ключа, d и n используются в качестве секретного ключа.
| Буквы алфавита | А | Б | В | Г | Д | Е | Ж | З | И | й | К | Л | М | Н | О | П | Р |
| Номер буквы | |||||||||||||||||
| Буквы алфавита | С | Т | У | Ф | Х | С | Ч | Ш | Щ | Ъ | Ы | Ь | Э | Ю | Я | ||
| Номер буквы |
5) Представим шифруемое сообщение как последовательность чисел в диапазоне от 0 до 32: 16, 17, 6, 5, 6, 12,
Для представления чисел в двоичном виде требуется 6 двоичных разрядов, так как в русском алфавите используются 33 буквы, поэтому исходный текст имеет вид: 010000, 010001, 000110, 000101, 000110, 001100.
Длина блока L определяется как минимальное число из целых чисел, удовлетворяющих условию L ³ log2(33+1); L=6
Теперь зашифруем сообщение, используя открытый ключ {7,33}
Y1 = (167) mod 33 =  ;
;
Y2 = (177) mod 33 =  ;
;
Y3 = (67) mod 33 =  ;
;
Y4 = (57) mod 33 = 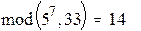 ;
;
Y5 = (67) mod 33 =  ;
;
Y6 = (12^7) mod 33 = 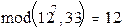 ;
;
Расшифруем полученные данные, используя закрытый ключ {3,33}.
Y1 = (253) mod 33 =  ;
;
Y2 = (83) mod 33 =  ;
;
Y3 = (303) mod 33 =  ;
;
Y4 = (143) mod 33 =  ;
;
Y5 = (307) mod 33 = 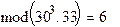 ;
;
Y6 = (123) mod 33 = 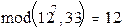 ;
;
Данные расшифрованы, сопоставим последовательность <16, 17, 6, 5, 6, 12> с последовательностью букв нашего алфавита. Получили слово ПРЕДЕЛ.
Задание 2. Хеширование и цифровая подпись документов.
Используя данные задания 2, получить хеш – код m для сообщения М при помощи хеш – функции Н, взятой из рекомендаций МККТТ Х.509. Вектор инициализации Н0 выбрать равным нулю.
Вычислить цифровую подпись методом RSA под электронным документом М, используя рассчитанный хеш – код m и секретный ключ d.
Представить схему цифровой подписи с подробным описанием ее функционирования.
Хеш – функцию МККТТ Х.509 запишем следующим образом:
Hi=[(Hi-1 Å Mi)2] (mod n), где i=l,n, H0 – вектор инициализации, Мi =М1,М2,М3…,Мn - -длина блока.
Все блоки делят пополам и к каждой половине прибавляют равноценное количество единиц. С преобразованными таким образом блоками производят интеграционные действия.
Необходимо получить хеш – код сообщения ПРЕДЕЛ при помощи хеш функции Х.509 с параметрами p=3, q=11.
Порядок вычисления хеш – кода:
А) получить значение модуля: n=pq= 3*11=33
Б)Представить сообщение в виде номеров букв русского алфавита в десятичном и двоичном видах:
П Р Е Д Е Л
16 17 6 5 6 12
00010000, 00010001, 00000110, 00000101, 00000110, 00001100.
В) Разбить байт пополам, добавив в начало полубайта единицы и получить хешируемые блоки Мi:
| M1 | M2 | M3 | M4 | M5 | M6 |
| M7 | M8 | M9 | M10 | M11 | M12 |
Г) Выполнить интеративные шаги:
Первая интерация
| М1 | |
| Å | |
| Н0=0 | |
| Н0 Å М1 | 11110001=24110 |
| [(H0Å M1)2] (mod 33) | 241 mod 33 = 10 |
| Н1 | 1010=00001010 |
Вторая интерация
| М2 | |
| Å | |
| Н1 | |
| Н1 Å М2 | 11111010=25010 |
| [(H1Å M2)2] (mod 33) | 250 mod 33 = 19 |
| Н1 |
Третья интерация
| М3 | |
| Å | |
| Н2 | |
| Н2 Å М3 | 11100010=22610 |
| [(H2Å M3)2] (mod 33) | 226 mod 33 = 28 |
| Н3 |
Четвертая интерация
| М4 | |
| Å | |
| Н3 | |
| Н3 Å М4 | 11101101=23710 |
| [(H3Å M4)2] (mod 33) | 237 mod 33 = 6 |
| Н4 |
Пятая интерация
| М5 | |
| Å | |
| Н4 | |
| Н4 Å М5 | 11110110=24610 |
| [(H4Å M5)2] (mod 33) | 246 mod 33 = 15 |
| Н5 |
Шестая интерация
| М6 | |
| Å | |
| Н5 | |
| Н5 Å М6 | 11111001=24910 |
| [(H5Å M6)2] (mod 33) | 249 mod 33 =18 |
| Н6 |
Седьмая интерация
| М7 | |
| Å | |
| Н6 | |
| Н6 Å М7 | 11100010 = 22610 |
| [(H6Å M7)2] (mod 33) | 226 mod 33 = 28 |
| Н7 |
Восьмая интерация
| М8 | |
| Å | |
| Н7 | |
| Н7 Å М8 | 11101001= 233 |
| [(H7Å M8)2] (mod 33) | 233 mod 33 = 2 |
| Н8 |
Девятая интерация
| М9 | |
| Å | |
| Н8 | |
| Н8 Å М9 | 11110010 = 24210 |
| [(H8Å M9)2] (mod 33) | 242 mod 33 = 11 |
| Н9 |
Десятая интерация
| М10 | |
| Å | |
| Н9 | |
| Н9 Å М10 | 11111101 = 253 |
| [(H9Å M10)2] (mod 33) | 253 mod 33 = 22 |
| Н10 |
Одиннадцатая интерация
| М11 | |
| Å | |
| Н10 | |
| Н10 Å М11 | 11100110 =23010 |
| [(H10ÅM11)2] (mod 33) | 230 mod 33 = 32 |
| Н11 |
Двенадцатая интерация
| М12 | |
| Å | |
| Н11 | |
| Н11 Å М12 | 11011100 = 22010 |
| [(H11ÅM12)2] (mod 33) | 220 mod 33 = 22 |
| Н12 |
Таким образом, исходное сообщение ПРЕДЕЛ имеет хеш – код m=22.
Для вычисления цифровой подписи используем следующую формулу:
S=md (mod n) = 223 mod 33 = 22
Пара (M, S) передается получателю как электронный документ М, подписанный цифровой подписью S, причем подпись S сформирована обладателем секретного ключа d.
Получив пару (M, S), получатель вычисляет хеш – код сообщения М двумя способами:
1) Восстанавливает хеш – код m’, применяя криптографическое преобразование подписи S с использованием открытого ключа e:
m’=Se (mod n) =227 mod 33 = 22
2) Находит результат хеширования принятого сообщения с помощью той же хеш – функции: m=H(M) =22.
При равенстве вычисленных значений m’ и m получатель признает пару (M, S) подлинной.
СПИСОК ЛИТЕРАТУРЫ
1. Романец Ю. В. Защита информации в компьютерных системах и сетях. /Под ред. В.Ф. Шаньгина. – М: Радио и связь 1999
2. Петраков А.В. Основы практической защиты информации. 2-е издание Учебн. Пособие. – М: Радио и связь 200
3. Защита информации в телекоммуникационных системах. Программа, метод. указ. и контр. Задания АИЭС 2006






