Идеальный газ как единая физическая система характеризуется макропараметрами, к которым относятся давление, объём и температура. Для экспериментального исследования свойств газов удобно зафиксировать значение одного из макропараметров и рассмотреть изменение двух других. Процессы в газе с неизменным количеством вещества, проходящие при фиксированном значении одного из макропараметров, называются изопроцессами.
Изотермический - это изопроцесс, протекающий при неизменной температуре (
). Он описывается законом Бойля-Мариотта: если температура данного количества газа не меняется, то произведение его давления на его объем постоянно: 
. Изотерма – график, показывающий зависимость давления от объема при постоянной температуре.
Изотерма представляет собой ветвь гиперболы. Чем выше температура процесса, тем дальше от координатных осей p,V расположена соответствующая ей изотерма.
Изобарный - это изопроцесс, протекающий при неизменном давлении (
). Он описывается законом Шарля: если давление данного количества газа не меняется, то отношение его объёма к температуре постоянно: 
. Изобара – график, показывающий зависимость объема от температуры при постоянном давлении.
Изобара представляет собой прямую линию. Чем выше давление процесса, тем больше наклон изобары к оси температур.
Изохорный - это изопроцесс, протекающий при неизменном объёме (
). Он описывается законом Гей-Люссака: если объём данного количества газа не меняется, то отношение его давления к его температуре постоянно: 
. Изохора – график, показывающий зависимость давления от температуры при постоянном объеме.
Изохора представляет собой прямую линию. Чем больше объем, тем больше наклон изобары к оси температур.
Покажем все графики изотермического, изобарного изохорного процессов в координатах (p, V), (V, T) и (p, T):
Экспериментальные газовые законы дают возможность получить уравнение состояния газа – функциональную зависимость между термодинамическими параметрами, характеризующими состояние системы.
Уравнение Клапейрона (уравнение состояния для фиксированного количества газа): при любом изменении состояния данного количества газа произведение давления на объем, деленное на абсолютную температуру, остается постоянным:
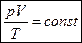
Уравнение Клапейрона - Менделеева (уравнение состояния для произвольного количества газа):
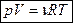, т.к. 
, то 
R – универсальная газовая постоянная; R=8,31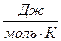 
Если газ находится в нормальных условиях, то его давление и температура строго фиксированы: p0=1,01∙105 Па, Т0=273 К (t0=0°С).
Физическая модель газа, для которого уравнение состояния выполняется точно, называется идеальным газом. Вследствие этого уравнение состояния Клапейрона – Менделеева называют уравнением состояния идеального газа.
Тема №5.
