Дифракция- это совокупность явлений наблюдающихся при распространении света в средах с резкими неоднородностями, причем размеры этих неоднородностей должны быть сравнимы с длиной волны.
В зависимости от фронта волны существует два вида дифракции:
Фраунгофера - она наблюдается на плоских поверхностях и удаленных источниках.
Френеля - на сферических поверхностях.
Явление дифракции было объяснено в сер. 19 в. Френелем, который в принцип Гюйгенса внес одно слово, что вторичные волны когерентны.
Принцип Гюйгенса-Френеля:
a) каждая точка до которой доходит волновое движение, служит центром вторичных волн;
b) огибающая этих вторичных волн дает положение фронта волны в следующий момент времени;
c) результирующая волна является суммой вторичных волн, которые складываются в соответствии с законом интерференции.
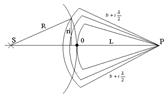Метод зон Френеля.
Пусть имеется источник S, который является точечным.
В какое-то время фронт волны – сфера. Разобьем поверхность волнового фронта таким образом, чтобы расстояние от края соседней зоны изменялось на 
.
Амплитуда результирующих колебаний в точке Р равна
Величина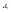 
зависит от площади i-ой зоны и угла между внешней нормалью к поверхности зоны в какой-либо ее точке и прямой, направленной из этой точки в точку Р.
Если площадь всех зон одинакова, то амплитуда волны, испускаемой каждой точкой, тоже одинакова, но в т.Р волна от каждой соседней зоны приходит с убывающей амплитудой. Амплитуды образуют арифметическую прогрессию, члены которой убывают:
Знаки ‘+’ и ‘-’ потому что рядом находящиеся зоны находятся в противофазе.
В световой волне действие всего бесконечного сферического волнового фронта эквивалентно действию половины волны первой зоны Френеля. Отсюда следует закон прямолинейного распространения света.
.
Дифракция Френеля на круглом отверстии.
Дифракционная картина наблюдается на экране Э. Экран параллелен плоскости отверстия L.
т.е.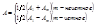 
.
Если m- нечетное, то в М наблюдается максимум; если m-четное – минимум.
При неизменном положении источника света, число зон зависит от диаметра отверстия и расстояния L. Следовательно при изменении диаметра или L результат в т.М должен изменится.
Если 
, то никакой интерференционной картины наблюдаться на экране не будет, в этом случае свет распространяется как и в отсутствие непрозрачного экрана с отверстием, т.е. прямолинейно.
Дифракция Френеля на небольшом диске.
Интерференционная картина на экране имеет вид концентрических темных и светлых пятен с центром в т.О, где всегда находится интерференционный минимум (пятно Пуассона). 
А- амплитуда света в т.О. При освещении диска белым светом в центре экрана наблюдается белое пятно, окруженное системой концентрических цветных колец.
По мере увеличения отношения диаметра диска d к расстоянию L от диска до экрана яркость пятна Пуассона постепенно уменьшается, а следующее за ним темное пятно расширяется, образуя область тени за диском.
13.Дифракция на одной щели. Как влияет на дифракцию Фраунгофера от одной щели увеличение длины волны и ширины щели?
Бесконечно длинную щель можно образовать, расположив рядом две обращённые в разные стороны полуплоскости.Следовательно, задача о дифракции Френеля от щели может быть решена с помощью спирали Корню.Волновую поверхность падающего света, плоскость щели и экран, на котором наблюдается дифракционная картина, будем считать параллельными друг другу.(рис1)
Для точки P, лежащей против середины щели, начало и конец результирующего вектора находятся в симметричных относительно начала координат точки спирали.
(рис2)
 |
Если сместиться в точку 
, лежащую против края щели, начало результирующего вектора переместится в середину спирали О.Конец вектора переместится по спирали в направлении полюса 
.При углублении в область геометрической тени начало и конец результирующего вектора будут скользить по спирали и в конце концов окажутся на наименьшем расстоянии друг друга.Интенсивность света достигнет при этом минимума.При дальнейшем скольжении по спирали начало и конец вектора снова отойдут друг от друга и интенсивность будет расти.Тоже самое будет происходить при смещении из точки P в противоположную сторону, так как дифракционная картина симметрична относительно середины щели.Если изменять ширину щели, сдвигая полуплоскости в противоположные стороны, интенсивность в средней точке Р будет пульсировать, проходя попеременно через максимумы (рис.1) и отличные от нуля минимумы (рис.3,4)
Френелевская дифракционная картина от щели представляет собой светлую(р.1) или тёмную(р.2) центральную полосу, по обе стороны которой распологаются симметричные относительно неё чередующиеся тёмные и светлые полосы.При большой ширине щели начало и конец результирующего вектора для точки Р лежат на внутренних витках спирали вблизи полюсов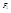 
и 
. Поэтому интенсивность света в точках, расположенных против щели, будет практически постоянной. Только на границах геометрической тени образуется система густо расположенных узких светлых и тёмных полос.
Как показывает формула 
,расстояние минимумов от центра картины возрастает с уменьшением 
. Таким образом, с уменьшением ширины щели центральная светлая полоса расширяется, захватывая всё большую и большую область экрана.Если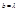 
, то 
,т.е. первый минимум соответствует углу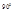 
; следовательно, он сдвинут на бесконечно удалённый край экрана. Освещённость экрана падает от центра к краям постепенно, асимптотически приближаясь к нулю; ширина центральной световой полосы возрастает беспредельно.Таким образом, с уменьшением b освещённость стремится стать равномерной по всему экрану.(рис5)
 |
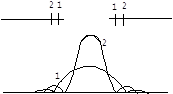Наоборот, при увеличении ширины щели положен8520/ие первых минимумов придвигается всё ближе и ближе к центру картины, так что центральный максимум становится всё резче и резче.При этом, относительная интенсивность максимума остаётся неизменной; абсолютная же величина его возрастает, ибо возрастает энергия, проходящая через уширенную щель. При очень широкой щели(по сравнению с 
) мы получаем в центре резкое изображение линейного источника.
14. Дифракционная решётка. Дисперсия и разрешающая сила дифракционной решётки. Укажите порядки главных максимумов, которые не могут наблюдаться на на дифракционной решётке с периодом d=9мкм и шириной одной щели b=3мкм.
Дифракционная решётка (одномерная) представляет собой систему параллельных щелей равной ширины, лежащих в одной плоскости и разделённых равными по ширине непрозрачными промежутками. Дифракция, наблюдаемая при прохождении света через такой спектральный прибор, имеет большое практическое значение.
Величина d=a+b называется периодом решётки или её постоянной. Разность хода лучей от 2-х соседних щелей будет 
Дифракционная картина на решётке определяется как результат взаимной интерференции волн, идущих от всех щелей. Поэтому в тех направлениях, в которых ни одна из щелей не распространяет свет, будут наблюдаться главные минимумы, определяемые условием: 
(m=1,2,3,….)
 |
Выражение 
(m=1,2,3,…..) задаёт условие главных максимумов. Т.к. 
, то число главных максимумов будет определяться выражением 
К тому же в направлениях, задаваемых условием: 
(m=1,2,3,…,N-1,N+1,…,2N-1,2N+1,…
мы получим дополнительные минимумы.
Для решётки из N щелей между 2-мя главными максимумами находится N-1 щелей, разделённых вторичными максимумами, создающими очень слабый фон. Т. о. чем больше щелей, тем больше образуется минимумов между главными максимумами, и тем более интенсивными и острыми будут сами максимумы.
Основными характеристиками дифракционной решётки являются дисперсия и разрешающая сила.
 |
Дисперсия решётки бывает угловая и линейная.
Угловая дисперсия определяет на какой угол расходятся лучи, длины волн которых отличаются на 1Ангстрем.
Линейная дисперсия: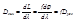 
, где f – фокусное расстояние проецирующей линзы.
Разрешающая способность: 
Растояние 
должно удовлетворять
условию Рэлея, т.е. минимум одного горба должен приходиться на максимум другого. Вывод разрешающей способности решётки:
Условия максимумов m-го порядка для лучей 1 и 2 будут
, 
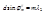
По условию Рэлея 
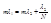или 
Для дифракционной решётки интенсивность главных максимумов будет выражаться следующим образом:
Т.к. при заданных d и b отношение d\b=3, то очевидно, что для любых m кратных 3 выражение под синусом будет кратно 
и следовательно интенсивность будет равна 0.
Т.о. для заданного соотношения d и b не может наблюдаться каждый 3-й максимум.
