На рис. 18 а изображена нагруженная в своей плоскости рама, вертикальные элементы которой имеют моменты инерции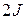 
, а горизонтальные элементы - 
. Требуется:
1) установить степень статической неопределимости и выбрать основную систему;
2) написать каноническое уравнение;
3) построить эпюры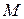 
от единичных сил и от заданной нагрузки;
4) найти перемещения;
5) построить окончательные эпюры внутренних силовых факторов: ,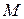 
и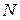 
для схемы на рис. 18а.
Пример. (рис. 18 а). Решение. Определяем степень статической неопределимости плоской рамы по формуле:
,
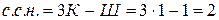где 
– количество замкнутых контуров; 
– количество простых шарниров (т.е. соединяющих два стержня), при этом надо помнить, что шарнирно-неподвижная опора считается как один простой шарнир, а шарнирно-подвижная – как два. Для получения основной системы отбросим в заданной системе две «лишние связи», превратив тем самым заданную статически неопределимую систему в определимую, и приложим лишние неизвестные 
и 
(рис. 18 б).
2. Система канонических уравнений метода сил для дважды статически неопределимой системы запишется в виде:
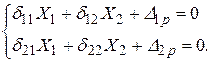
Рис. 18. Заданная и основная системы, единичные и грузовые эпюры 
, 
и 
3. Построение эпюр изгибающих моментов от единичных сил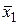 
=1,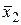 
=1 и заданной нагрузки проводится по известным правилам, установленным для балок (условимся строить эпюры М со стороны сжатых волокон).
Стержень BD 
;
, 
кН.м.
Стержень DC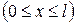 
кН.м.
Стержень CA 
;
кН.м;
.
Единичная эпюра представлена на рис. 18 б.
Стержень DC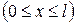
;
кН.м.
Стержень CA
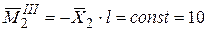кН.м.
Единичная эпюра представлена на рис. 18 г.
Аналогичным образом построены эпюры (рис. 18 д).
Стержень DC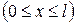
;
, 
кН.м.
Стержень CA
кН.м.
4. Определяем перемещения, входящие в канонические уравнения, пользуясь правилом Верещагина, по которому интегралы Мора находятся путем перемножения эпюр (при вычислении используем таблицу 3 в приложении).
Главные переменные 
и 
получим путем умножения единичных эпюр и самих на себя:
;
.
Побочные перемещения 
получим путем умножения эпюр на (знаки минус приняты в том случае, если сопрягаемые эпюры отложены в разные стороны):
.
Перемещения от внешней нагрузки 
и 
получим при перемножении эпюр на на соответственно:
;
.
Подставляя полученные коэффициенты в систему канонических уравнений метода сил, и сокращая 
, получим систему
решая которую, найдем лишние неизвестные
=16,5 и 
= 14.
5. Строим окончательные эпюры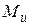 
, и 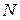для основной системы.
Стержень BD
;
; 
кН.м;
кН;
кН (сжатие).
Стержень DC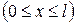
;
кН.м;
кН.м.
Исследуем кривую на экстремум
м;
кН.м;
;
кН;
кН;
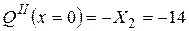кН (сжатие).
Стержень CA
;
кН.м;
кН;
кН (сжатие).
Эпюры 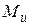, и 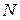представлены соответственно на рис.19 а, б, в.
Рис. 19. Окончательные эпюры 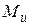, и 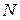и узлы рамы C и D
Проверку правильности построения окончательной эпюры изгибающих моментов осуществляем путем перемножения окончательной эпюры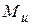 
на одну из единичных эпюр, например, эпюры моментов от силы 
. В результате такого перемножения получим перемещение рамы в точку В по направлению отброшенной горизонтальной связи. Если подсчитанное таким образом перемещение получится равным нулю, значит задача решена верно.
что составляет ~54%, т.е. приблизительно равно 0.
На рис. 19 г, д вырезаны узлы рамы C и D, к которым приложены все внутренние силовые факторы.
Задача 12
