Задачи, приводящие к понятию производной
I Задача о касательной
Определение. Касательной к линии L в ее точке М 0 называется предельное положение секущей M 0 M, когда точка M вдоль линии L стремится произвольным образом к совпадению с точкой M 0.
Чтобы придать математическую строгость этому определению, будем считать, что линия L – это график некоторой функции 
.
Пусть 
– фиксированная точка графика, а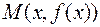 
–текущая точка. Обозначим 
. Стремление точки M к М 0 равносильно 
или 
. Через точку М 0 проходит много прямых, все они отличаются друг от друга угловыми коэффициентами. Касательная к графику в точке М 0 – это та прямая, угловой коэффициент которой есть предел углового коэффициента
секущей M 0 M при :
II Задача о скорости
Пусть по прямой, на которой выбраны начало отсчета, единица измерения и направление, движется точка по закону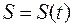 
(
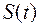– это координата точки на прямой в момент времени t). Важной характеристикой движения является скорость. Для равномерного движения (т.е. движения с постоянной скоростью) можно взять произвольный промежуток времени 
и разделить пройденный путь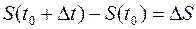 
на длительность промежутка времени, т.е. на 
. Именно потому, что скорость постоянная, полученный ответ не будет зависеть ни от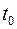 
, ни от 
.
В общем случае движения с переменной скоростью отношение 
есть не что иное как средняя скорость движения за промежуток . Средняя скорость тем лучше характеризует движение, чем меньше длительность . Устремляя к нулю, мы и получим мгновенную скорость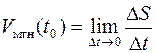 
.
Замечание. Две различные задачи, рассмотренные выше, привели в процессе решения к одному и тому же результату – пределу отношения приращения функции к приращению аргумента при условии, что последнее стремится к нулю. Имеется много задач в самой математике и в ее приложениях, которые приводят к необходимости вычисления таких пределов.
Определение и смысл производной
Рассмотрим функцию , определенную в точке 
и в некоторой ее окрестности. Придадим аргументу x приращение 
, не выводящее аргумент за пределы окрестности. Функция получит приращение 
.
Определение. Предел отношения приращения функции 
к приращению аргумента при 
(если этот предел существует) обозначается 
и называется производной функции 
по переменной в x точке x 0.
Итак, по определению
.
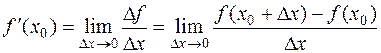Из определения следует, что производная – это число. Однако чаще всего оказывается, что это число можно вычислить не только в одной точке x 0, а во всех точках некоторого интервала. Тем самым на этом интервале определяется некоторая новая функция, которая тоже называется производной функции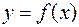 
и обозначается: 
. Кроме этих обозначений используются и другие:
– производная как функция (читается “дэ игрек по дэ икс”),
– производная в фиксированной точке x 0.
Сравнивая результаты, полученные в §1, с определением производной, можно придать производной смысл:
1) если 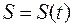– закон движения, то 
;
2) – это угловой коэффициент (тангенс угла наклона к оси Ox) касательной к графику функции 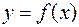в точке с абсциссой x 0.
Используя 2) легко написать уравнение касательной:
и нормали, т.е. прямой, проходящей через точку касания перпендикулярно касательной:
.
Пример. Вычислить (по определению) производную функции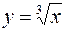 
.
Замечание 1. Производную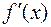 
удобно понимать как скорость изменения функции относительно аргумента x.
Замечание 2. Отношение приращения функции к приращению аргумента называют разностным отношением функции.
