ДИФЕРЕНЦІАЛЬНЕ ЧИСЛЕННЯ ФУНКЦІЇ ОДНІЄЇ ЗМІННОЇ
Методичні вказівки
для виконання практичних робіт
з дисципліни “Вища математика”
для студентів за спеціальностями
6.092602 “Гідромеліорація“ та
6.092102 “Промислове та цивільне будівництво“
Херсон – 2012
УДК 512(07); 514(07); 517(07)
Степаненко Н.В., Григоренко В.В. Методичні рекомендації щодо вивчення навчального модуля з дисципліни «Вища математика» із застосуванням кредитно-модульної системи організації навчального процесу – Херсон, ХДАУ, РВЦ «Колос», 2012 р.
Методичні вказівки до проведення практичних занять з дисципліни
Вища математика
Затверджено на кафедрі вищої математики Херсонського державного аграрного університету. Протокол № 1 від 26.01.2012 р.
Рекомендовано до друку методичною комісією Економічного факультету Херсонського державного аграрного університету.
Протокол №_ 1 від 24.01.2012 р.
Рецензент: доктор технічних наук, професор Марасанов В.В.
Методичні рекомендації призначені для підготовки, оформлення та викладання дисципліни «Вища математика» за кредитно-модульною системою в навчальному процесі.
© Григоренко В.В., 2012
©
Заняття 1.
Тема: Похідна функції. Основні поняття.
Означення. Похідною функції у = f(х) називають границю відношення приросту функції до приросту аргументу, якщо приріст аргументу прямує до нуля:
у′ = 
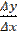 .
.
Знаходження похідної називають диференціюванням функції. 
Похідну функції позначають y′ або, або f′(x).
Властивості (правила знаходження) похідної:
1) (Cu)′ = Cu′;
2) (u+v-w)′ = u′+v′-w′;
3) (uv)′ = u′v+uv′;
4) 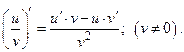
Таблиця похідних основних елементарних функцій:
1) (С)′ = 0, (С = const);
2) (х)′ = 1;
3) 
4) 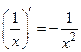 ;
;
5) 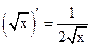 ;
;
6) 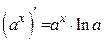 ;
;
7) ( ex )′ = ex;
8)  ;
;
9) 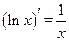 ;
;
10) ( sin x )′ = cos x;
11) ( cos x )′ = - sin x;
12) (tg x)′ = 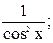 ;
;
13) (ctg x)′ = - 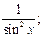 ;
;
14) (arctg x)′ = 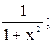 ;
;
15) (arcctg x)′ = - 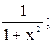 ;
;
16) (arcsin x)′ = 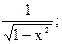 ;
;
17) (arccos x)′ = - 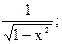 .
.
Приклади:
Знайти похідні функцій:
1. 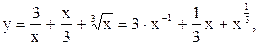
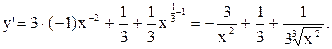
2. 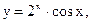
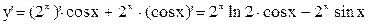
3. 

Завдання для роботи в аудиторії:
Знайти похідні функцій:
1) y = 2х3 _ 5х2 + 7х - 12;
2) y = х -  х2 +
х2 +  х3 -
х3 - 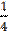 х4;
х4;
3) y =  2
2  -
-  + 8;
+ 8;
4) y = 6  + 5
+ 5 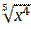 - 7
- 7 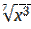 ;
;
5) y = tgx – ctgx;
6) y =  +
+ 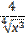 -
- 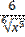 ;
;
7) y = 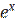 (х2 – 2х + 6);
(х2 – 2х + 6);
8) y = (8х5 – 3х + х4) 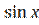 ;
;
9) y = 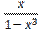 ;
;
10) y = 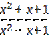 ;
;
11) y = 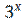 (
(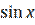 -
- 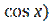 ;
;
12) у = 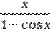 ;
;
13) у =  ;
;
14) у = x2 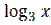 ;
;
15) у = х 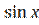 arctg х.
arctg х.
16) у = 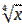 arctg x;
arctg x;
17) у = 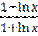 ;
;
18) у =  ;
;
19) у = 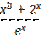 ;
;
20) у = х3 ( - 4).
- 4).
Домашнє завдання:
Знайти похідні функцій:
1) у = х4 – 4х6 + 9х5 + 2х7 – 2х – 42;
2) у =  -
- 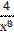 +
+ 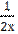 ;
;
3) у = 15 - 3  +
+ 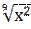 +
+ 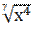 ;
;
4) у = 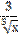 -
- 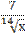 -
-  + 0,75;
+ 0,75;
5) у = 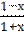 ;
;
6) у = (х2 – 3х + 3)(х2 +2х – 1);
7) у = 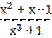 ;
;
8) у = 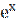
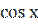 ;
;
9) у = 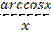 ;
;
10) у=(2х3+3)arccosx.
Заняття 2
Тема: Похідна складної функції.
Якщо у = f(u) і u = 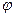 (х) – диференційовані функції своїх аргументів, то похідна функції від функції (або складної функції) у = f(
(х) – диференційовані функції своїх аргументів, то похідна функції від функції (або складної функції) у = f(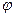 (x)) існує і дорівнює добутку похідної даної функції у по аргументу
(x)) існує і дорівнює добутку похідної даної функції у по аргументу 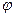 (х) і похідної
(х) і похідної 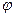 (х) по х: у′=f′(
(х) по х: у′=f′(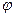 (х))
(х)) 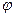 ′(х).
′(х).
Таблиця похідних складних функцій:
1) (un)′ = nun-1 u;
2) ( ′ = -
′ = -  ;
;
3) (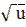 )′ =
)′ =  ;
;
4) (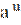 )′ =
)′ = 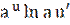 ;
;
5) (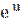 )′ =
)′ = 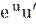 ;
;
6) 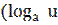 )′ =
)′ = 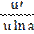 ;
;
7)  )′ =
)′ = 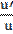 ;
;
8)  )′ = -
)′ = - 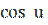 u′;
u′;
9) (tg u)′ = 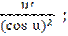
10)  ctg u)′ = -
ctg u)′ = - 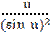 ;
;
11) (arcsin u)′ =  ;
;
12) (arccos u)′ = -  ;
;
13) (arctg u)′ = 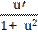 ;
;
14) (arcctg u)′ = - 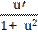 .
.
Приклад:
Знайти похідну функції у = 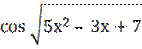 ;
;
у′=- 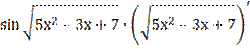 =-
=- 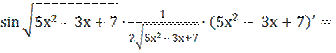
- 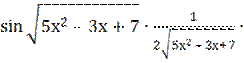 (10х – 3) = -
(10х – 3) = - 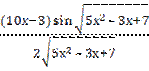 .
.
Завдання для роботи в аудиторії:
Знайти похідні функцій:
1) у = 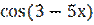 ;
;
2) у = 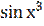 ;
;
3) у = 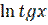 ;
;
4) у = 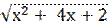 ;
;
5) у = ( )2;
)2;
6) у = (2х3 + 3х2 + 6х +1)4;
7) у = 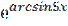 ;
;
8) у = (7 +  )3;
)3;
9) у = 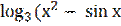 );
);
10) у = 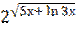 ;
;
11) у = (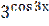 + (
+ (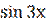 )2)3;
)2)3;
12) у = 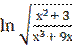 ;
;
13) у = 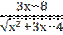 ;
;
14) у =  ;
;
15) у = (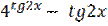 )5;
)5;
16) y = ( –
– 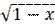 )4;
)4;
17) y =  ;
;
18) y = ( +
+ 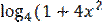 ))6;
))6;
19) y = 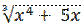 -
- 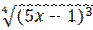 ;
;
20) y= 
Домашнє завдання:
Знайти похідні функцій:
1) у = (2 – 3х)5;
2) у = (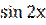 )2;
)2;
3) у = 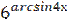 ;
;
4) у =  ;
;
5) у = 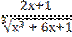 ;
;
6) у =  ,
,
7) у = (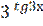 -
- 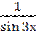 )5;
)5;
8) у =  ;
;
9) у = х 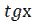 +
+ 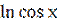 +
+ 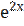 ;
;
10) у =  .
.
Заняття 3
Тема: Похідні неявних функцій і функцій,заданих параметрично. Похідна функції у = 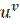 .
.
Функція у(х) називається неявною, якщо залежність між х і у виражена рівнянням F(х;у)= 0, яке не розв’язане відносно у.
Щоб знайти похідну від неявної функції, треба дане рівняння продиференціювати, вважаючи у функцією від х, і одержане рівняння розв’язати відносно похідної у ′. Похідна неявної функції виражається через незалежну змінну х і саму функцію у.
Приклад:
Знайти похідну функції
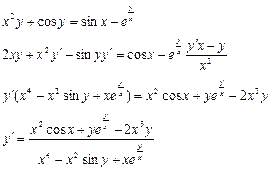
Якщо функція задана параметрично: 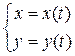 , де х(t) і у(t) – диференційовані функції, то її похідна:
, де х(t) і у(t) – диференційовані функції, то її похідна: 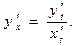
Приклад:
Знайти похідну функції 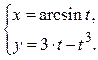
х ′(t) = 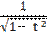 , у′(t) = 3 - 3 t2 = 3(1 – t2);
, у′(t) = 3 - 3 t2 = 3(1 – t2);
у′(х) = 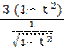 = 3(1 – t2)
= 3(1 – t2) 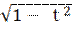 .
.
Похідна степенево-показникової функції у = 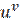 , де u і v – диференційовані функції від х, знаходиться за формулою:
, де u і v – диференційовані функції від х, знаходиться за формулою:
у′ = v 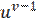
 u′ +
u′ + 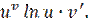
Приклад:
Знайти похідну функції у = 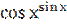 .
.
у′ = 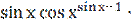 (-
(- 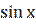 ) +
) + 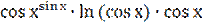 =
= 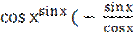 )+ +
)+ + 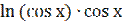 ) =
) = 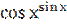 (
(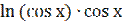 – tg х).
– tg х).
Завдання для роботи в аудиторії:
Знайти похідні функцій:
1) х2 + 5ху + у2 – 7 = 0;
2) у2 + ху + 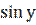 = 0;
= 0;
3) 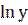 + ху – 5 = 0;
+ ху – 5 = 0;
4) х4 + у4 = х2у2;
5) у3 + 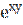 = 0;
= 0;
6) 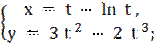
7) 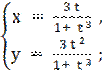
8) 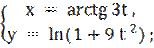
9) 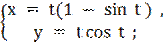
10) 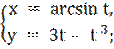
11) у = 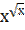 ;
;
12) у = 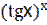 ;
;
13) у = 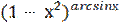 ;
;
14) у = 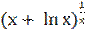 ;
;
15) у = 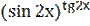 .
.
Домашнє завдання:
Знайти похідні функцій:
1) х3у3 – 2ху +3 = 0;
2)  – arctgу = 0;
– arctgу = 0;
3) 2 + tgх - 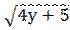 = 0;
= 0;
4) х = ctg t, у = 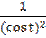 ;
;
5) 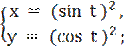
6) у = 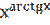 ;
;
7) у = 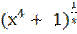 ;
;
8) у = 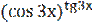 ;
;
9) у = 
Заняття 4
Тема: Похідні вищих порядків. Диференціал функції.
Похідною другого порядку або другою похідною функції у = f(х) називається похідна від її похідної: у′′ = (f′(х))′. Позначається: у′′ або f′′(х) або  .
.
За аналогією визначаються і позначаються похідні третього, четвертого і вищих порядків: у′′′, 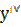 ,…,
,…, 
Для функції, заданої параметрично, похідна другого порядку знаходиться за формулою: у′′(х) =  .
.
Приклади:
1) Знайти похідну третього порядку функції: у = х2 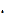
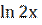 .
.
у′ = (х2  = 2х
= 2х 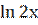 + х2
+ х2 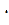
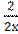 = 2х
= 2х 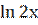 + х;
+ х;
у′′ = (2х 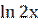 +х)′ = 2
+х)′ = 2 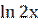 + 2х
+ 2х  +1 = 2
+1 = 2 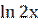 + 2 +1 = 2
+ 2 +1 = 2 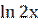 +3;
+3;
у′′′ = (2 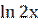 +3)′ = 2
+3)′ = 2 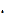
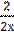 =
= 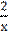 .
.
2) Знайти похідну другого порядку функції: х = 2 t - 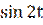 , у=8
, у=8  .
.
х′(t) = 2 - 2 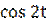 = 2(1 -
= 2(1 - 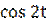 ) = 2
) = 2 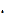 2
2 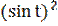 = 4
= 4 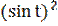 ;
;
х′′(t) = 4 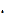 2
2 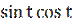 = 8
= 8 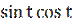 ;
;
у′(t) = 24 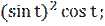
у′′(t) = 24(2 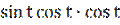 -
- 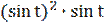 ) = 24
) = 24 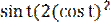 -
- 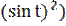 =
=
= 24  (
( - 1 +
- 1 + 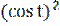 ) = 24
) = 24  (3
(3 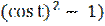 ;
;
у′′(х) = 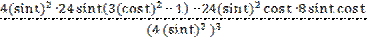 =
=
= 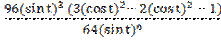 =
= 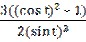 = -
= - 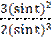 = -
= - 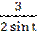 .
.
3) Знайти  , якщо
, якщо 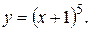
Знаходимо послідовно першу, другу і третю похідні:
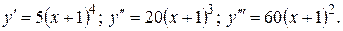
Диференціалом функції у= f(х) називається добуток її похідної на приріст незалежної змінної: dу = у′ 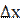 або dу = у′dх, так як
або dу = у′dх, так як 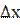 = dх. Із цієї формули отримуємо, що у′ = f′(х) =
= dх. Із цієї формули отримуємо, що у′ = f′(х) = 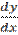 .
.
Приклади:
1. Знайти диференціал функції: у = 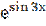 .
.
у′ = 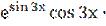 3 = 3
3 = 3 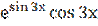 ;
;
dу = 3 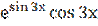 dх.
dх.
2. Обчислити диференціали першого, другого та третього порядків функції 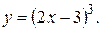
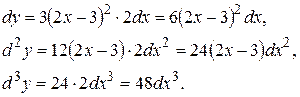
3. Обчислити наближене значення площі круга, радіус якого рівний 3,02 м.
Скористаємося формулою 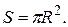 Покладаючи
Покладаючи 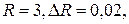 маємо
маємо 
І тому наближене значення площі круга складає 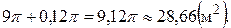
Завдання для роботи в аудиторії:
І. Знайти другу похідну функцій:
1) у = 4х2 – 2х + 3;
2) у = 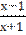 ;
;
3) у = (1 + х2)  х;
х;
4) 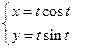 ;
;
5) х =  , у =
, у = 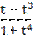 ;
;
6) 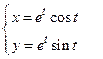
ІІ. Знайти похідні вказаних порядків:
1) у = х5 + 6х2 – 5х + 8, у(5) -?
2) у = 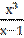 , у′′′ -?
, у′′′ -?
3) y = x2 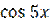 , y(4) -?
, y(4) -?
4) y = 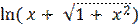 , y′′ -?
, y′′ -?
5) y = 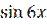 , y(5) -?
, y(5) -?
ІІІ. Знайти диференціали функцій:
1) у = arcctg4х;
2) у = 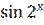 ;
;
3) у =  ;
;
4) у = 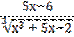 ;
;
5) у = 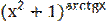 .
.
Домашнє завдання:
І. Знайти похідні вказаних порядків:
1) у = х5 – 4х4 + 2х3 – 3х2 + 7х – 9, у(4) -?
2) у = 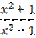 , у′′ -?
, у′′ -?
3) у = (3х + 10)6, у′′′ -?
4) у = х 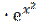 , у′′ -?
, у′′ -?
5) х = t3 + 1, у = t2 + t + 1, у′′(х) –?
6) х =  , у = t - arcctg t, у′′(х) –?
, у = t - arcctg t, у′′(х) –?
ІІ. Знайти диференціали функцій:
1) у = (х2 + 4х + 1)(х2 -  );
);
2) у = 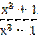 ;
;
3) у = 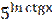 ;
;
4) у = 3х2 - 4  +
+ 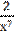 .
.
Заняття 5




