А) Перевірка гіпотези про вид закону розподілу досліджуваної величини

Лабораторна робота №2

Перевірка статистичних гіпотез

Мета роботи Ознайомитись з базовими поняттями перевірки статистичної гіпотези. Оволодіти навичками застосування критерію "хі-квадрат" та використання коефіцієнта конкордації для перевірки статистичної гіпотези в галузях міжнародних відносин.

Короткі теоретичні відомості

Статистичних гіпотез завжди дві і вони взаємовиключні. Одну з них називають нульовою гіпотезою Н₀, а другу – альтернативною гіпотезою Н_1, що завжди протилежна нульовій.

Якщо сформульовані гіпотези Н₀ – основна та Н₁ альтернативна (конкуруюча) і обраний критерій перевірки справедливості основної гіпотези, то прийняття Н₀ позначає відкидання Н₁, а відкидання Н₀ позначає справедливість Н₁.

Ймовірність відкидання гіпотези Н₀, якщо вона справедлива, називається ймовірністю помилки першого роду або рівнем значущості і позначається 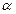. Величина 1- 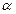є ймовірністю прийняття справедливої гіпотези і називається рівнем довіри. Ймовірність прийняття гіпотези Н₀, якщо вона не вірна, називається ймовірністю помилки другого роду і позначається 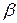. Величина 1- 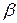є ймовірністю відкидання невірної гіпотези і називається потужністю критерію.

а) Перевірка гіпотези про вид закону розподілу досліджуваної величини

Припустимо, що з деякої генеральної сукупності Х, яка розглядається як випадкова величина, обрана вибірка 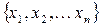. За даними вибірки побудовано статистичний ряд (табл. 2.1), що містить варіанти х_i та відповідні частоти п_i, 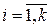, k – кількість варіант у випадку дискретного ряду. У випадку інтервального ряду х_i – середини інтервалів, k – кількість інтервалів.

 

Таблиця 1

хi	х 1	х 2	…	хk
пi	п 1	п 2	…	пk

Отриманий на основі вибіркових даних статистичний ряд називається емпіричним законом розподілу величини Х.

За даними статистичного ряду можна знайти числові характеристики, які є Закон розподілу випадкової величини Х, параметрами якого є відповідні вибіркові числові характеристики, називається теоретичним законом розподілу.

При здійсненні такої заміни немає впевненості, що закон розподілу обраний правильно. Тому розроблено процедуру, яка дозволяє оцінити ступінь відповідності обраного закону даним вибірки. Критерії здійснення такої перевірки називаються критерії згоди, найбільш відомим з яких є критерій Пірсона 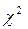(хи-квадрат).

Критерій Пірсона 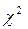обчислюється за формулою:

, (1)

де 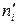– частоти, отримані за теоретичним законом розподілу (теоретичні частоти).

З формули (1) видно, що у випадку, коли відповідні теоретичні та емпіричні частоти співпадають, χ ²=0. Тобто чим ближче χ ² до нуля, тим краще узгоджуються вибіркові дані та обраний теоретичний закон розподілу.

Розраховане значення критерію χ ² порівнюється з його критичним значенням 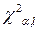, яке знаходиться за статистичними таблицями або за допомогою вбудованої статистичної функції Excel ХИ2ОБР(, l). Параметрами функції ХИ2ОБР є: – рівень значущості; l – ступені волі, l 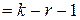, де k – кількість груп емпіричного розподілу, r – кількість параметрів теоретичного розподілу (наприклад, для нормального розподілу r =2, оскільки параметрів два – а і ). Якщо 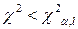, то гіпотеза про закон розподілу приймається. У противному випадку гіпотеза відкидається.

Зауваження. У деяких статистичних таблицях критичне значення χ ² надається залежно від рівня довіри , =1- .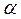

перевірка гіпотези про закон розподілу величини Х здійснюється за такими етапами:

1) З генеральної сукупності Х здобувається вибірка і будується статистичний ряд.

2) Висувається гіпотеза про закон розподілу випадкової величини Х.

3) Знаходяться вибіркові параметри обраного закону розподілу.

4) Розраховуються теоретичні частоти.

5) Розраховується критерій χ ² за формулою (2.1).

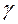6) Обирається рівень значущості (або рівень довіри ) і знаходиться критичне значення 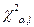(або ).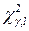

7) Порівнюються розраховане і критичне значення критерію χ ² і робиться висновок про справедливість висунутої гіпотези.

 

б) Перевірка гіпотези про рівність генеральних дисперсій. F-критерій (Фішера)

Перевірка гіпотези про рівність генеральних дисперсій здійснюється за F-критерієм (Фішера) тільки тоді, коли статистичні дані незалежні і розподілені за нормальним законом. Формулюються гіпотези:

Н₀ – дисперсії двох нормально розподілених генеральних сукупностей рівні, тобто ;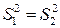

Н₁ - дисперсії двох нормально розподілених генеральних сукупностей не рівні, тобто .

F-критерій (Фішера) розраховується за формулою:

, (2)

Гіпотеза Н₀ приймається, якщо розраховане значення F менше критичного значення розподілу Фішера F_крит, взятого із рівнем значущості і ступенями волі l ₁ та l ₂ для чисельнику і знаменнику відповідно: l ₁= п ₁ – 1, l ₂= п ₂ – 1, де п ₁, п ₂ – об’єми вибірок. F_крит можна знайти за допомогою вбудованої статистичної функції Excel FРАСПОБР (; l ₁; l ₂).

Зауваження. Дисперсія у чисельнику дроби у формулі (2) повинна бути більше дисперсії у знаменнику, тобто значення F-критерію повинно бути більше одиниці.

В) Перевірка гіпотези про рівність генеральних дисперсій. Критерій Зігеля-Тьюкі

Якщо статистичні дані не розподілені за нормальним законом або виміряються з використанням порядкової шкали, то перевірка гіпотези про рівність генеральних дисперсій здійснюється за критерієм Зігеля-Тьюкі. Формулюються гіпотези:

Н₀ – дисперсії двох генеральних сукупностей рівні, тобто ;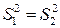

Н₁ - дисперсії двох генеральних сукупностей не рівні, тобто .

Перевірка виконується за даними двох вибірок за такими етапами:

1) Формується об’єднана вибірка.

2) Даним об’єднаної вибірки присвоюються ранги (порядкові номери) за правилом: найменшому значенню присвоюється ранг 1, двом найбільшим – ранги 2 і 3; наступним двом найменшим – ранги 4 і 5; наступним найбільшим – ранги 6 і 7 і т. д. При цьому, якщо кількість елементів вибірки непарна, то її центральний елемент (тобто медіана) не отримує ніякого рангу.

3) Розраховуються суми рангів елементів вихідних вибірок .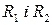

4) Розраховується нормальна випадкова величина Z за формулою:

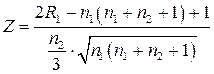, (3)

де п ₁, п ₂ – об’єми вибірок. При цьому – сума рангів меншої за об’ємом вибірки. Якщо 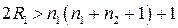, Z розраховується за формулою:

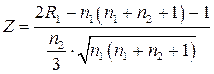. (4)

5) У випадку, коли перевіряються вибірки різних об’ємів, обчислюється скоректована нормальна випадкова величина 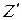за формулою:

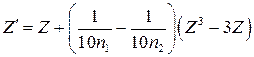. (5)

6) Обирається рівень значущості .

7) За допомогою таблиці значень функції нормального розподілу або вбудованої функції Excel НОРМРАСП знаходиться ймовірність Р (Z) або Р ().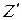

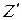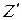8) Порівнюються рівень значущості і величина 2 Р (Z) (2 Р ()). Якщо 2 Р (Z)> (або 2 Р ()> ), то гіпотеза Н₀ про рівність генеральних дисперсій приймається.

Зауваження. Для перевірки правильності присвоєння рангів можна скористатися формулами: 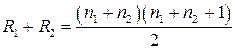у випадку парної кількості елементів об’єднаної вибірки; 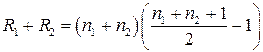у випадку непарної кількості цих елементів.