Вариант № 1.
Задача № 1:
Из точки, находящейся на середине радиуса дискообразной платформы, вращающейся с угловой скоростью w рад/с, вертикально вверх подбрасывается тело. Принимая ускорение свободного падения g и пренебрегая сопротивлением воздуха, определить начальную скорость подбрасывания, при которой тело упадёт на край.
(4 балла)
Задача № 2:
Две лодки движутся навстречу друг другу по инерции параллельными курсами с одинаковыми скоростями 1 м/с. Из первой лодки общей массой 200 кг. сначала выбрасывается перпендикулярно движению груз массой 20 кг., а затем из встречной лодки в неё тоже перпендикулярно движению перебрасывается груз такой же массы. Определить скорость первой лодки после перебрасывания в неё груза.
(3 балла)
Задача № 3:
Из шланга конец которого находится на уровне земли, бьёт струя воды, наибольшая высота подъёма которой над землёй 5 м., а радиус кривизны в верхней точке 30 м. Площадь поперечного сечения шланга 5 см^2. Принимая g = 10 м/с^2, определить массу воды, находящейся в воздухе.
(5 баллов)
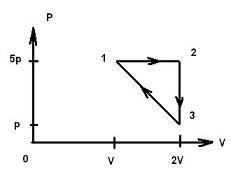
Задача № 4:
Найти КПД тепловой машины, совершающей циклический процесс 1-2-3-1, представленный на диаграмме p-V. Рабочее тело – идеальный одноатомный газ.
(6 баллов)
Задача № 5:
В калориметр теплоёмкостью 1700Дж/кг, содержащий лёд массой 1 кг при температуре равной -10С, впускается пар при температуре 100С. В результате в системе устанавливается температура 20С. Определить массу впущенного пара. Удельная теплоёмкость воды 4200 Дж/(кг*К), удельная теплоёмкость льда 2100 Дж/(кг*К), удельная теплота плавления льда 3.3*10^5 Дж/кг, удельная теплота парообразования воды 22.6*10^5.
(3 балла)
Задача № 6 (Сложная):
Автомобиль движется по закруглению шоссе, имеющему радиус кривизны R=50 м.
Уравнение движения автомобиля: (t)=A+Bt+Ct2, где A=10 м, B=10 м/с, C=-0,5 м/с2.
Найти:
1) скорость v автомобиля, его тангенциальное a, нормальное an и полное a ускорения в момент времени t=5 с;
2) длину пути s и модуль перемещения |r| автомобиля за интервал времени =10 с,
отсчитанный с момента начала движения.
Вариант № 2.
Задача № 1:
Автобус, ехавший со скоростью 54 км/ч, начал тормозить за 200 м до остановки. Найдите его ускорение при этом.
Задача № 2:
Третьей космической называется скорость, которую необходимо сообщить телу на орбите Земли, чтобы оно навсегда покинуло пределы Солнечной системы; она равна примерно 16 км/с. Земля вращается вокруг Солнца со скоростью около 30 км/с. Почему же она не улетает от него?
Задача № 3:
Посадочный модуль приближается к земле вертикально с ускорением 2 м/с2. Найдите вес космонавта массой 80 кг.
Задача № 4:
Как движется тело (траектория, скорость, ускорение...), на которое действует единственная сила — постоянная по величине и направленная перпендикулярно скорости тела?
Задача № 5:
Максимально полно изложите третий закон Ньютона.
Задача № 6:
Ребенок качается на качелях, пролетая нижнюю точку со скоростью 4 м/с. Во сколько раз его вес при этом больше, чем в неподвижном положении? Расстояние от точки подвеса до сидения качелей 2 м.
Задача № 7:
В каком движении тело может находиться без воздействия на него каких-либо сил?
Задача № 8:
Чему равна равнодействующая сил действия и противодействия?
Задача № 9:
Учебный самолет массой 2 т летит на высоте 420 м со скоростью 360 км/ч. Снижаясь с выключенным двигателем, он приземляется со скоростью 108 км/ч. Найдите работу силы сопротивления воздуха.
Задача № 10:
Пластилиновые шарики массой 30 г со скоростью 20 м/с и массой 70 г со скоростью 10 м/с летят навстречу друг другу. Найдите их скорости после столкновения и количество выделившегося при этом тепла.
Задача № 11:
Какую работу А против сил поверхностного натяжения надо совершить, чтобы, выдувая мыльный пузырь, увеличить его диаметр от 1 см до 11 см? Поверхностное натяжение мыльного раствора 0.043 Н/м.
Решение:
Изменение площади поверхности пузыря до и после совершения работы
S = S2 - S1 = 4(r22 - r12) = (d22 - d12)
Т.к. у оболочки мыльного пузыря две поверхности (наружняя и внутренняя), то совершенная работа находится
A =2a S = 2a(d22 - d12) = 0,0032 (Дж)
Ответ: А = 3,2·10-2 Дж
Задача № 11 (сложная):
Маховик, вращавшийся с постоянной частотой n0=10 с-1, при торможении начал вращаться равнозамедленно. Когда торможение прекратилось, вращение маховика снова стало равномерным, но уже с частотой n=6 с-1. Определить угловое ускорение? маховика и продолжительность t торможения, если за время равнозамедленного движения маховик сделал N=50 оборотов.
Вариант № 3.
Задача № 1:
На улице идёт дождь. В каком случае ведро, стоящее в кузове грузового автомобиля, наполнится быстрее водой: когда автомобиль движется, или когда стоит?
Задача № 2:
На гладком горизонтальном столе покоится стальной шарик. На него одновременно налетают с двух сторон два шарика таких же размеров и масс, но один из них стальной, а другой сделан из резины. Считая удары лобовыми и абсолютно упругими, найти скорости всех трёх шаров после разлёта. Жёсткость резины намного меньше жёсткости стали.
Задача № 3:
Груз массы 3 кг поднимают и опускают при помощи лёгкой нити и блока, ось которого закреплена неподвижно. Однажды блок «заело» — он перестал вращаться вокруг своей оси. При этом удаётся поднимать груз силой 40 Н, приложенной к свободному концу нити, груз в этом случае движется вверх с постоянной скоростью 0,1 м/с. Какое количество тепла выделится в системе за 3 с подъёма?
Задача № 4:
Моток медной проволоки имеет массу 300 г и электрическое сопротивление 57 Ом. Определите длину проволоки и площадь её поперечного сечения.
Задача № 5:
Какая сила необходима для вытаскивания из доски гвоздя длиной 120 мм, если он забит 12 ударами молотка массой 0,5 кг при скорости молотка перед ударом 5 м/с. Силу сопротивления считать не зависящей от направления движения.
Задача № 6:
В двух одинаковых сосудах находятся одинаковые массы кислорода и азота. Давление кислорода равно 1 атм, давление азота 3 атм. Сосуды соединяют тонкой трубкой, газы перемешиваются. Каким станет давление в системе после установления равновесия? Теплообмен с окружающей средой пренебрежимо мал. Молярная масса кислорода 32 г/моль, азота 28 г/моль.
Задача № 7:
Амперметр «тепловой» системы измеряет текущий через него ток по выделяемому в его внутреннем сопротивлении количеству тепла. В проводимом эксперименте текущий через амперметр ток периодически меняет и величину и направление: в течение 0,2 с он равен 2 А, следующие 0,1 с ток течёт в другую сторону и равен 1 А. Затем снова 2 А, потом 1 А и т. д. Какой ток показывает при этом амперметр?
Задача № 8 (сложная):
Кинематическое уравнение движения материальной точки по прямой (ось x) имеет вид x = A + Bt + Ct2,
где A=5 м, В=4 м/с, С=-1 м/с2.
1. Построить график зависимости координаты x и пути s от времени.
2. Определить среднюю скорость v за интервал времени от t1 = 1 с до t2 = 6 с.
3. Найти среднюю путевую скорость v за тот же интервал времени.
+
++






