Методика формирования понимания абстрактности числа
Предварительная работа
После обучения приемам счета, в процессе формирования счетной деятельности, знакомства с отношениями между числами, сравнения множеств по количеству на основе счета показываем, что число предметов в группе не зависит от их качественных признаков (формы, размера, цвета и др.) и их пространственного расположения. Это помогает детям научиться воспринимать число как абстрактное математическое понятие — количественную характеристику множества, раскрывает закон сохранения количества. Данная работа полезна для развития абстрактного мышления у дошкольников.
Методика обучения
В процессе практических упражнений с предметами, картинками, геометрическими фигурами показываем независимость числа сначала от размеров предметов, затем от расстояния между предметами, потом от конфигурации их расположения и обсуждаем это. Сначала рассматриваем равночисленные множества, затем неравночисленные.
Независимость числа от размера предметов
Наглядный материал
Одинаковые предметы двух контрастных размеров, расположенные так, чтобы не прослеживалось приложение и действительно казалось, что одних предметов больше, чем других.
Фрагмент 1
— Что это (рис.)?
— Чем отличаются?
— Какие по размеру?
— Каких квадратов кажется больше?
— Каких квадратов кажется меньше?
— Что нужно сделать, чтобы узнать точно?
— Посчитайте!
— По скольку их?
— Квадратов по пять, значит поровну.
— Почему мы вначале ошиблись?
— Больших квадратов кажется больше, маленьких квадратов
кажется меньше, но их поровну, потому что по пять.
— Как, не считая, проверить? (Приложением.)
Фрагмент 2
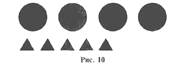—Что это (рис. 10)?
— Чем отличаются?
— Какие по размеру?
— Каких фигур кажется больше?
— Каких фигур кажется меньше?
— Что нужно сделать, чтобы узнать точно?
— Посчитайте!
— Какое число больше, 5 или 4?
— Какое число меньше?
— Значит, чего больше? Чего меньше?
— Почему мы вначале ошиблись?
— Кругов кажется больше, потому что они большие, треугольников кажется меньше, потому что они маленькие. Посчитав, можно узнать точно: кругов меньше, а треугольников больше, потому что 4 < 5, а 5 > 4.
- Как, не считая, проверить? (Приложением.)
Задание студентам: Напишите самостоятельно схему диалога.
Схема:
— Что это?
— Чем отличаются?
— Чего кажется больше?
— Чего кажется меньше?
— Как узнать точно?
— Посчитайте!
— Какое число больше?
— Какое число меньше?
— Значит, чего больше?
— Чего меньше?
— Почему мы ошиблись вначале?
— Как, не считая, проверить?
Независимость числа от расстояния между предметами
Наглядный материал
Две группы предметов одинаковых по величине, расположенных на разном расстоянии («далеко — близко») (рис.).
Схема
— 
Что это?
— Как расположены?
— Чего кажется больше?
— Чего кажется меньше?
— Как узнать точно?
— Посчитайте!
— По скольку?
— По пять — значит, поровну.
— Почему мы ошиблись вначале?
Замечание: нельзя проверять приложением, так как теряется смысл задачи.
Независимость числа от формы расположения предметов
Наглядный материал
Две группы предметов, одинаковых по величине, расположенных по разному (в ряд, по кругу и др.). Например, на рис. 12 можно выбрать две группы геометрических фигур.
Схема
— 
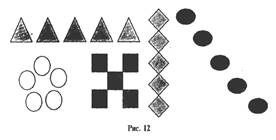Что это?
— Как расположены?
— Чего кажется больше?
— Чего кажется меньше?
— Как узнать точно?
— Посчитайте!
— Какое число больше?
— Какое число меньше?
— Значит, чего больше?
— Чего меньше?
— Почему мы ошиблись вначале?
Усложнения
1. Идем от равночисленных множеств к неравночисленным.
2. Увеличиваем количество элементов в сравниваемых
множествах от 1 до 10.
3. Даем сразу несколько отличий.
Схема
— 
Что это?
— Как расположены?
— Чего кажется больше?
— Чего кажется меньше?
— Как узнать точно?
— Посчитайте!
— По скольку?
— По пять — значит, поровну.
— Почему мы ошиблись вначале?
Замечание: нельзя проверять приложением, так как теряется смысл задачи.
