Основные правила дифференцирования

Лекция 12. Производная функции

Понятие производной

Определение. Если отно­ше­ние имеет предел при этот предел называ­ют производной функции 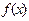при заданном значении 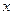и за­пи­сывают

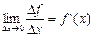. (1)

Замечание. Если при не­ко­то­ром значении 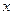, су­щест­ву­ет производная функции 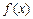при этом значении, то в этой точке функция непрерывна.

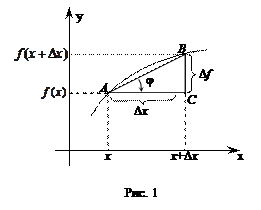
Заметим, что отношение 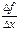из рис. 1 численно равно .

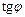Определение. Производная функции в точке 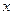численно равна тан­генсу угла, который составляет касательная к графику этой функции по­строенной в точке 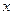с положительным направлением с осью .

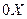Из последнего определения ста­но­вится ясно, почему в случае убы­ва­ю­щей функции (рис. 2) про­из­вод­ная от­ри­цательна. Это объясняется тем, что , если будет отрицатель­ным.

На этом свойстве производной осно­ва­но исследование поведения функции на возрастание (убывание) на заданном отрезке.

 

Производные простейших функций

 

Используя определение производной и правил вычисления пределов, най­дем производные простейших функций.

1. , где – некоторая постоянная. По определению производной из (1) получаем удобную формулу

, (2)

тогда из (2) имеем , т.е. 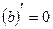. Про­из­вод­ная постоянной величины равна 0.

2. 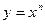, где – любое число. Из формулы (2) имеем

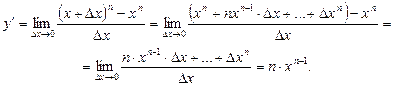
Т.е. .

3. .

Т.е. .

Остальные производные простейших функций (табл.1) приведем без вывода

Таблица 1

Производные простейших функций

Функция	Производная	Функция	Производная
С
,
,

 

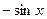
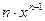
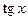
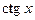
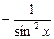
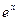
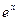
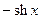
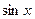
Основные правила дифференцирования

Пусть заданы две функции и , которые имеют про­из­вод­ные в точке .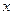

1. Производная алгебраической суммы равна алгебраической сумме производных. .

Покажем это. Пусть некоторая функция у, равная имеет приращение . Тогда функции и тоже должны получить приращения 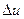и , соответственно. Новое значение будет , а для – , следовательно,

Найдем по определению (2) производной

.

 

2. Производная произведения равна . Покажем спра­вед­ли­вость этого равенства.

Если, как в первом случае, дать 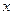приращение 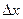, то функции u и v также получат приращение, следовательно, и функция тоже изменится. Найдем .

.

По определению производной

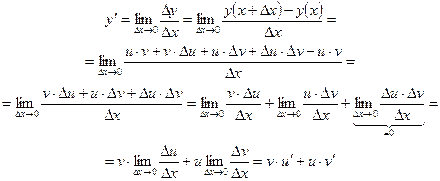
Если необходимо вычислить производную нескольких сомножителей, например, 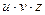, если все три функции имеют производные в точке 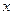, используя правило вычисления производной для двух сомножителей, получим

3. Производная частного. Рассмотрим функцию , причем, кроме су­щес­твования производных в точке 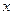для функций и необходимо по­ло­жить, что в точке 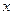отлична от нуля.

Найдем .

и тогда из определения производной имеем

.

Пример. Показать, что .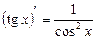

Решение. Используя производную частного

4. Производная сложной функции. Пусть дана , где . Тогда имеет место теорема, которую приведем здесь без доказательства.

Теорема. Если функция имеет в точке производную и функция имеет в точке производную 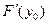, тогда сложная функция имеет в точке производную, равную

(3)

Пример. Найти производную функции .

Решение. .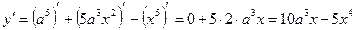

 

Пример. Найти производную функции .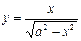

Решение.

Пример. Найти производную сложной функции .

Решение.

5. Логарифмическое дифференцирование. Пусть дана функция . При этом предполагается, что функция не обращается в нуль в точке . Покажем один из способов нахождения производной функции , если очень сложная функция и по обычным правилам диф­фе­рен­цирования найти производную затруднительно.

Так как по первоначальному предположению не равна нулю в точке, где ищется ее производная, то найдем новую функцию и вычислим ее производную

. (4)

Отношение 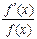называется логарифмической производной функции . Из формулы (4) получаем

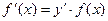. (5)

Формула (5) дает простой способ нахождения производной функции .

Пример. Найти производную сложной функции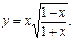

Решение. Для нахождения используем формулу (5). Предварительно прологарифмируем функцию

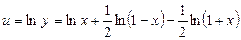
и найдем производную полученной функции

.

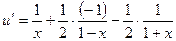Теперь по формуле (5) получаем

.

Пример. Найти производную сложной функции .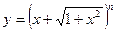

Решение. В связи с тем, что указанная функция сложная, воспользуемся логарифмическим дифференцированием, для чего предварительно прологарифмируем нашу функцию

.

Найдем производную полученной функции по формуле (5).

.

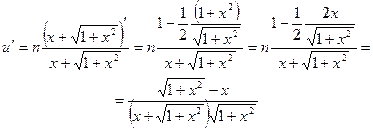6. Производная обратной функции.

Теорема. Если имеет в точке производную, отличную от нуля, тогда в этой точке обратная функция также имеет производную и имеет место соотношение

. (6)

Пользуясь этой теоремой, найдем производные обратных три­го­но­мет­ри­чес­ких функций.

1. на интервале . , тогда , от­ку­да сле­до­ва­тель­но, .

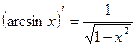2. . . , откуда

3. 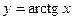. ; , откуда

4. ; ;

5. , где и являются функциями от 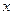. Для нахождения применим формулу (5). Для этого предварительно найдем функцию

и ее производную

.

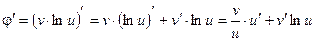По формуле (5) получаем .

Эту же формулу можно получить иначе. Представим в виде

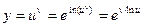
и найдем производную этой функции

.

В заключение этой лекции приведем таблицу основных формул дифференцирования (табл.2).

Таблица 2.