МЕТОДИЧЕСКИЕ УКАЗАНИЯ
к лабораторным работам
по курсу “ Радиационная безопасность ”
для студентов всех специальностей дневной формы обучения
г. Витебск
2012 г.
СОДЕРЖАНИЕ
| Введение……………………………………………………….. | |
| Статистическая обработка результатов…………………. | |
| 1. Лабораторные работы……………………………….…….. | |
| Лабораторная работа № 1. Определение мощности экспозиционной дозы …………………...………………………. | |
| Лабораторная работа № 2. Определение мощности полевой эквивалентной дозы ………………………………………….. | |
| Лабораторная работа № 3. Определение плотности потока бета-излучения с поверхности ……………………………..... | |
| Лабораторная работа № 4. Определение удельной и объемной активности в твердых и жидких пробах …………..……….. | |
| Лабораторная работа № 5 Определение активности радионуклидов в объектах окружающей среды гамма-радиометром РУГ-91М1 «АДАНИ» …………............................................. | |
| Лабораторная работа № 6 Определение мощности экспозиционной и эквивалентной доз прибором «РД-1503» «Радекс» …………………………………………………......... |
ВВЕДЕНИЕ
Проведение лабораторного практикума по курсу “Радиационная безопасность” позволяет решить следующие задачи:
1. Дать понятие о естественном и техногенном фоне, естественных и искусственных радионуклидах.
2. Ознакомить студентов с различными дозиметрическими величинами и методами их определения.
3. Привить навыки работы как с простейшими бытовыми дозиметрическими приборами, так и с более сложными стационарными радиометрами.
4. Помочь разобраться в особенностях детектирования различных видов ионизирующих излучений.
5. Научить студентов определять плотность потока бета-излучения с поверхностей, а также объемную и удельную активность радионуклидов в твердых и жидких пробах.
Исходя из поставленных задач, при подготовке к выполнению каждой работы студентам необходимо обращать особое внимание на теоретическую часть, в которой содержатся данные, позволяющие лучше понять физический смысл проводимых измерений.
По каждой лабораторной работе студент должен оформлять отчет, содержащий следующие обязательные разделы:
1. Дата выполнения.
2. Название работы.
3. Теоретическое обоснование.
4. Порядок подготовки приборов и выполнения работы.
5. Математическую обработку полученных результатов или расчетную часть на основе полученных результатов.
6. Выводы по результатам работы.
Если отчеты оформлены без соответствия вышеизложенным требованиям, то работа не допускается к защите пока не будут устранены обнаруженные недостатки.
Отчеты оформляются на листах формата А-4 или в отдельных тетрадях с оформлением титульного листа общего на все работы.
При выполнении лабораторных работ студенты должны выполнять следующие требования:
· бережно относиться к приборам и оборудованию;
· не включать приборы без разрешения преподавателя или лаборанта;
· закончив измерение, сразу выключать питание приборов;
· обнаружив неисправность прибора, немедленно сообщать об этом преподавателю или лаборанту.
В лаборатории студенты должны соблюдать следующие меры предосторожности:
· при измерении плотности потока бета-излучения с поверхности контейнера с радиоактивным источником не открывать упаковочный полиэтиленовый пакет и сам контейнер, а также не класть его на край стола, чтобы избежать случайного падения; закончив измерения сразу же сдать контейнер преподавателю;
· при проведении измерений плотности потока с экрана монитора очень аккуратно снимать и устанавливать защитный стеклянный экран, чтобы он не разбился;
· при работе на стационарном радиометре КРВП-3Б, прежде чем включать питание, обязательно проверить наличие заземления;
· при проведении измерения объемной и удельной активности стараться избегать попадания исследуемых веществ на кожу рук и одежду, а после завершения работы обязательно помыть руки с мылом.
СТАТИСТИЧЕСКАЯ ОБРАБОТКА РЕЗУЛЬТАТОВ
Статистическая обработка результатов имеет две основные задачи:
· представить результаты нескольких измерений в компактной форме;
· оценить надежность полученных результатов, т.е. степень их соответствия истинному значению определяемой величины.
Для решения этих задач необходимо предварительно оценить значимость и воспроизводимость полученных результатов.
Значимость результатов оценивается если в серии параллельных определений один из результатов представляется сомнительным, т.к. довольно значительно отличается от всех других результатов. Чтобы решить, оставлять этот результат для вычисления среднего или отбросить как промах оценивается его значимость с помощью Q-критерия, который также называют критерием значимости:
, (0.1)
где x1 - сомнительный результат (наименьший и (или) наибольший из всех измеренных);
x2 - результат, который ближе всего к x1 по значению;
R - размах варьирования - разность между предельными значениями определяемой величины, т.е. максимальным и минимальным значениями.
Вычисленное значение Q-критерия сравнивают с табличным значением, которое определяется по таблице 1 в зависимости от числа измерений n и доверительной вероятности Р, которая обычно принимается равной 0.95. Сомнительный результат следует отбросить, если Q > Qтабл., в противном случае, его оставляют для дальнейших расчетов. При проверке значимости результатов Р=0.95 означает, что при Q < Qтабл. результат будет значим не менее, чем в 95 случаях из 100.
Таблица 0.1- Значения Qтабл. для Р=0,95 и различных n
| n | ||||||||
| Q | 0,94 | 0,77 | 0,64 | 0,56 | 0,51 | 0,48 | 0,44 | 0,42 |
Используя только значимые результаты находят среднее значение по формуле:
, (0.2)
xi - каждый значимый результат;
n - количество значимых результатов.
Зная среднее значение можно оценить воспроизводимость результатов, т.е. степень близости отдельных результатов к среднему значению. Количественной характеристикой воспроизводимости является стандартное или средне-квадратичное отклонение, которое рассчитывается по формуле:
, (0.3)
где xi - каждое измеренное значение;
- среднее значение;
n - число измерений.
Стандартное отклонение равно 0 если каждое единичное измерение равно среднему значению, т.е. при абсолютной воспроизводимости. Следовательно, чем больше величина стандартного отклонения, тем хуже воспроизводимость результатов.
Квадрат стандартного отклонения называют дисперсией и также может рассматриваться как характеристика воспроизводимости:
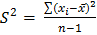, (0.4)
где xi - каждое измеренное значение;
- среднее значение;
n - число измерений.
Соотношение дисперсий двух рядов называется критерием Фишера (F -критерием) и позволяет определить принадлежат ли эти ряды к одной генеральной совокупности.
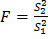, (0.5)
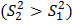
Вычисленный F-критерий сравнивают с табличным значением, приведенным в таблице 2, которое зависит от заданной доверительной вероятности (обычно принимают Р=0.95) и числа измерений.
Таблица 0.2 - Значение F-критерия для Р=0,95 при различном количестве измерений
| n2 | n1 | ||||||
| 1.9 | 1.9 | 1.9 | 19.15 | 19.3 | 19.35 | ||
| 9.5 | 9.3 | 9.1 | 9.0 | 8.9 | 8.85 | ||
| 7.0 | 6.7 | 6.4 | 6.3 | 6.2 | 6.0 | ||
| 5.8 | 5.5 | 5.2 | 5.1 | 5.0 | 4.9 | ||
| 5.1 | 4.8 | 4.5 | 4.4 | 4.3 | 4.2 | ||
| 4.7 | 4.4 | 4.1 | 4.0 | 3.9 | 3.8 |
Если вычисленный F-критерий меньше табличного значения, то можно считать, что оба ряда значений характеризуют одну и ту же генеральную совокупность.
Пользуясь найденным значением стандартного отклонения можно оценить надежность единичного и среднего результата, решив тем самым одну из главных задач статистической обработки.
Под оценкой надежности результатов понимают нахождение доверительных границ. Доверительные границы - это пределы области вокруг экспериментально найденного единичного или среднего результата, внутри которой следует ожидать с заданной степенью доверительной вероятности нахождения истинного значения единичного или среднего результата. Вероятность нахождения истинного значения в доверительном интервале задается через коэффициент нормированных отклонений t, который определяется по таблице 3 в зависимости от доверительной вероятности и числа степеней свободы (n - 1).
Таблица 0.3 - Значение коэффициента нормированных отклонений при различной доверительной вероятности
| n-1 | Значения t при разных Р (%) | n-1 | Значения t при разных Р (%) | ||||
| 99.9 | 99.9 | ||||||
| 12.7 | 63.7 | 2.31 | 3.36 | 5.04 | |||
| 4.3 | 3.92 | 31.6 | 2.26 | 3.25 | 4.78 | ||
| 3.18 | 5.84 | 12.9 | 2.23 | 3.17 | 4.59 | ||
| 2.78 | 4.6 | 8.6 | 2.2 | 3.11 | 4.44 | ||
| 2.57 | 4.03 | 6.86 | 2.18 | 3.06 | 4.32 | ||
| 2.45 | 3.71 | 5.96 | 2.16 | 3.01 | 4.22 | ||
| 2.36 | 3.5 | 5.4 | 2.14 | 2.98 | 4.14 |
Интервал, ограниченный этими пределами называют доверительным интервалом.
В случае малой выборки, доверительные границы находят из следующих уравнений.
Для единичного определения:
, (0.6)
где t - коэффициент нормированных отклонений (принимаем его значение при Р=95%),
S - стандартное отклонение.
Для среднего из нескольких определений:
(0.7)
где t - коэффициент нормированных отклонений,
S - стандартное отклонение,
n - число измерений.
Таким образом статистическая обработка позволяет оценить значимость, воспроизводимость и надежность полученных результатов.
Зная доверительные границы, легко можно найти погрешность измерений в процентах по формуле:
(0.8)
где t - коэффициент нормированных отклонений,
S - стандартное отклонение,
n - число измерений.
ЛАБОРАТОРНАЯ РАБОТА № 1
