Методика выполнения работы. Указание по мерам безопасности

Указание по мерам безопасности

При выполнении лабораторной работы

 

Внутри используемых в работе электроизмерительных приборов имеется переменное сетевое напряжение 220 В, 50 Гц, представляющее опасность для жизни.

Наиболее опасными местами являются сетевой выключатель, гнезда предохранителей, шнур сетевого питания приборов, соединительные провода, находящиеся под напряжением.

К выполнению лабораторных работ в учебной лаборатории допускаются обучающиеся прошедшие обучение по мерам безопасности при проведении лабораторных работ с обязательным оформлением в журнале протоколов проверки знаний по мерам безопасности при проведении лабораторных работ.

Перед выполнением лабораторной работы обучающимся
необходимо:

- усвоить методику выполнения лабораторной работы, правила ее безопасного выполнения;

- ознакомиться с экспериментальной установкой; знать безопасные методы и приемы обращения с приборами и оборудованием при выполнении данной лабораторной работы;

- проверить качество сетевых шнуров; убедиться, что все токоведущие части приборов закрыты и недоступны для прикосновения;

- проверить надежность соединения клемм на корпусе прибора с шиной заземления;

- в случае обнаружения неисправности немедленно доложить преподавателю или инженеру;

- получить у преподавателя допуск к ее выполнению, подтверждая этим усвоение теоретического материала. Обучающийся не получивший допуск к выполнению лабораторной работы не допускается.

Включение приборов производит преподаватель или инженер. Только после того, как он убедится в исправности приборов и правильности их сборки можно приступать к выполнению лабораторной работы.

При выполнении лабораторной работы обучающиеся должны:

- не оставлять без присмотра включенные приборы;

- не наклоняться к ним близко, не передавать через них какие-либо предметы и не опираться на них;

- при работе с грузиками надежно закреплять их крепежными винтами на осях.

замену любого элемента установки, присоединение или разъединение разъемных соединений производить только при отключенном электропитании под четким наблюдением преподавателя или инженера.

Обо всех недостатках, обнаруженных во время выполнения лабораторной работы, сообщить преподавателю или инженеру

По окончании работы отключение аппаратуры и приборов от электросети производит преподаватель или инженер.

Лабораторная работа №11

ИЗУЧЕНИЕ СВЯЗАННЫХ КОЛЕБАНИЙ

Цель работы:

Изучить основные закономерности гармонических колебаний и сложение колебаний одного направления. Изучить колебания связанных маятников, синфазные и противофазные колебания, биения.

Теория

Введение. Движения, называемые колебаниями, широко распространены и играют большую роль в природе и технике. Характерной особенностью всех колебательных движений является их периодичность, т.е. регулярная повторяемость через равные промежутки времени Т. В качестве примеров колебательных движений можно указать: движение маятника, колебание тела на пружине, движения поршня в двигателе внутреннего сгорания, колебания атомов и молекул вблизи положения равновесия в твердых телах и т.д. Математически повторяемость движения означает выполнение следующих соотношений:

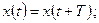
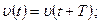(1)

 

Где x – координата колеблющейся точки, и a – скорость и ускорение колеблющейся точки соответственно. Аналогичные соотношения могут быть записаны и для любых других параметров, описывающих движение колеблющейся точки. Отрезок времени Т, между двумя последовательными одинаковыми состояниями движения колеблющегося тела, называют периодом колебаний. Следует отметить, что повторяемость движения присуща также равномерному вращению. Однако, при вращательном движении все точки тела движутся по неизменным круговым траекториям все время в одну и ту же сторону, в то время как при колебательном движении одна и та же траектория проходится колеблющимся телом поочередно в противоположных направлениях.

К колебательным относят и такие движения, которые не являются строго периодическими в указанном выше смысле, но для которых характерно то, что движущееся тело проходит через равные промежутки времени через положение равновесия, двигаясь поочередно в противоположных направлениях, и достигая через такие же промежутки времени максимального отклонения от равновесия в том или ином направлении. Примером такого движения могут быть затухающие колебания маятника (колебания с постепенно убывающей амплитудой колебаний). Колебательное движение считается заданным, если известны координаты тела как функция времени.

Свободные гармонические колебания. Колебания называются гармоническими, если их можно описать с помощью функций синуса или косинуса. Свободные колебания наблюдаются в системе, на которую не действуют внешние силы или их действие скомпенсировано, и при отсутствии в системе сил трения. В качестве примера гармонических колебаний рассмотрим свободные колебания математического маятника.

Математиче с кий маятник – материальная точка, подвешенная на невесомой и нерастяжимой нити (рис. 1).

Вследствие того, что нить нерастяжима расстояние от материальной точки до точки подвеса О остается постоянным и траектория по которой движется материальная точка – окружность. Таким образом, материальная точка совершает вращательное движение, для описания движения материальной точки воспользуемся основным законом динамики вращательного движения:

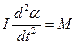(2)

Здесь I – момент инерции тела относительно оси вращения, a – угол отклонения маятника от положения равновесия, M – результирующий момент сил, действующих на тело. Для материальной точки момент инерции .

На материальную точку действуют две силы – сила тяжести и сила натяжения нити . Однако, в уравнение входят не силы, действующие на материальную точку, а моменты сил относительно оси вращения О. Т.к. линия действия силы проходит через точку О, то плечо этой силы (т.е. кратчайшее расстояние от оси вращения до линии действия силы) равно нулю и момент силы также равен нулю. Момент силы тяжести относительно оси О вычисляется по формуле mg l Sinα. Ограничимся рассмотрением малых углов α ≤ 7 – 8 °. При таких малых углах Sinα ≈ tgα ≈ α, если угол α выразитьв радианах. Кроме того, из физических соображений запишем момент силы тяжести со знаком «минус», учитывая тот факт, что момент силы тяжести действует в сторону, противоположную отклонению. С учетом всего сказанного, уравнение (2) можно представить в следующем виде

(3)

преобразуем его, перенеся все члены в левую сторону и разделив уравнение на m и l:

(4)

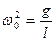Введем обозначение, тогда уравнение примет вид:

 

(5)

 

Уравнение (5) называется уравнением свободных колебаний и играет важное значение в теории колебаний. Решением этого уравнения является гармоническая функция вида:

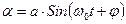(6)

То, что (6) является решением уравнения (5), можно легко проверить прямой подстановкой (6) в (5), которая превращает уравнение (5) в тождество. Кроме того, в приложении 1 приведено строгое решение уравнения (5). Следует иметь ввиду, что решение (6) может быть представлено как с помощью функции синус, так и с помощью функции косинус, различными при этом окажутся лишь начальные фазы 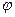, значения которых можно найти, используя, например, начальные условия.

В уравнении (6) α – это угол отклонения маятника от положения равновесия в момент времени t, а –представляет собой максимальное отклонение тела от положения равновесия и называется амплитудой колебаний. Аргумент функции синус – называется фазой колебания; - круговая или циклическая частота колебаний, t – время, j - начальная фаза (значение фазы при t = 0). Легко установить связь между циклической частотой колебаний и периодом колебаний Т. Так как через промежуток времени Т колебания полностью повторяются, то, следовательно, должно повторяться и значение координаты α, т.к. функция Sin является периодической с периодом 2p, то должно выполняться соотношение:

(7)

; где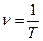

Величина называется частотой и равна числу колебаний в единицу времени. Соответственно, равно числу колебаний, совершаемых за секунд.

Т.о., тело, уравнение движений которого имеет вид (5), действительно совершает гармонические колебания с круговой частотой . Частота называется собственной частотой системы, а колебания, которые совершает система, выведенная из состояния равновесия в отсутствие сил трения и других внешних воздействий, называются свободными колебаниями.

Сложение колебаний. Рассмотрим сложение двух колебаний, происходящих в одном направлении вдоль оси х, при условии, что амплитуды этих колебаний одинаковы и равны а, а частоты отличаются незначительно. Покажем, что результирующее движение при этих условиях можно рассматривать как гармоническое колебание с пульсирующей амплитудой. Такое колебание с периодически изменяющейся (пульсирующей) амплитудой называется биениями.

Обозначим частоту одного из колебаний буквой , а частоту второго колебания через . Будем предполагать, что 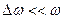. Положим начальные фазы обоих колебаний равными нулю. Тогда уравнения колебаний будут иметь следующий вид:

(8)

 

Складывая эти выражения и применяя тригонометрическую формулу для суммы косинусов, получаем:

(9)

(во втором множителе мы приняли 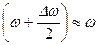, т.е. пренебрегли членом , малым по сравнению с ).

График функции (9) изображен на Рис. 2 (график построен для ). Заключенный в скобки множитель в формуле (9) изменяется гораздо медленнее, чем второй множитель. Ввиду условия 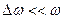за то время, за которое множитель 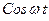совершает несколько полных колебаний, множитель, стоящий в скобках, почти не изменится. Это позволяет рассматривать колебание (9) как гармоническое колебание с частотой , амплитуда которого изменяется по некоторому периодическому закону.

Рис. 2.

По определению амплитуда всегда положительна, поэтому выражение (9) можно интерпретировать как:

(10)

 

где - скачок фазы, изменяющийся на при каждом прохождении амплитудой через нулевое значение, при таком подходе считают, что при прохождении амплитуды через нулевое значение фаза колебания скачком изменяется на π.

Связанные колебания. Под числом степеней свободы понимают число независимых координат, которые полностью задают положение системы в пространстве. Совокупность двух или нескольких маятников, каким-либо образом связанных между собой, представляет связанную систему. Связанными называются колебания, возникающие в такой системе, при условии взаимного влияния колебаний маятников друг на друга.

В механике простейшую систему с двумя степенями свободы образуют два одинаковых математических маятника массой m и длиной l, совершающие колебания в одной плоскости и связанные между собой невесомой пружинкой с коэффициентом жесткости k. Пружина находится на расстоянии d от точек подвеса. При движении маятников в одной вертикальной плоскости (см. рис.3) состояние системы полностью описывается двумя независимыми параметрами (координатами) - углами j₁ и j_2, задающими отклонения маятников от вертикали, т.е. данная система имеет две степени свободы.

Уравнения движения для каждого маятника можно получитьиз основного закона динамики вращательного движения:

(11)

 

Рис.3.

где 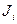- момент инерции i -го маятника относительно оси вращения; -сумма моментов сил, действующих на i -й маятник относительно этойже оси; j_i - угол поворота, применительно к каждому маятнику. На каждый маятник действует момент силы тяжести (перед ним стоит знак минус, т.к. он направлен в сторону противоположную отклонению) и момент сил со стороны пружины. С учетом сказанного, уравнение (11) для малых колебаний каждого из маятников (Sinj» j) имеет вид:

(12)

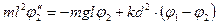
или после небольших преобразований:

(13)

поскольку момент инерции J точечной массы m, находящейся на расстоянии l от оси вращения, равен ml². Здесь учтено, что момент сил со стороны пружины, при малых j₁ и j₂ выражается через удлинение пружины, которое равно d(j₁ - j₂) и, следовательно, момент М упругой силы равен k×d(j₁ - j₂)×d, т.к. плечо этой силы равно d. Будем рассматривать случай, когда моменты сил трения, действующих на маятник, много меньше М и затуханием можно пренебречь.

Система уравнений (13) путем почленного сложенияи вычитания уравнений может быть преобразована к виду:

(14)

Введя новые переменные Q₁ и Q₂: Q₁ = j₁ + j₂; Q₂ = j₁ - j₂, мы получим следующую систему уравнений:

(15)

 

Т.о. система уравнений (13) в результате преобразований распалась на два независимых уравнения (15), каждое из которых представляет собой уравнение свободных колебаний вида (5), с собственными частотами (они называются нормальными), соответственно:

; (16)

Общие решения уравнений (15) будут иметь вид:

(17)

 

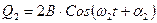
Здесь для удобства амплитуды обозначены 2А и 2В, а начальные фазы — a₁ и a₂. Обратный переход к углам отклонения маятников j₁ и j₂ дает:

(18)

 

Таким образом, в общем случае колебания каждого маятника складываются из двух независимых колебаний с нормальными частотами , и 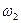, которые определяются выражениями (16).

Как видно из (18), возможны случаи, когда оба маятники одновременно колеблются лишь с одной из нормальных частот (т.е. при В = 0 или А = 0), Каждая из возможностей осуществляется в зависимости от способа возбуждения колебаний в системе, т.е. от начальных условий. Поскольку начальные отклонения и скорости маятников в общем случае имеют вид:

 

(19)

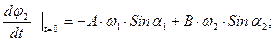
отсюда легко видеть, что случай В = 0 означает, что в начальный момент оба маятника были отклонены на один и тот же угол и имели одинаковые скорости .

Этот случай соответствует так называемым синфазным колебаниям, оба маятника колеблются с меньшей из нормальных частот _.

Случай А = 0 означает, что в начальный момент маятники были отклонены на одинаковые углы в противоположные стороны j₁₀ = - j₂₀ = В Cos a₂ и имели противоположные угловые скорости 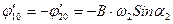. При таком способе возбуждения оба маятника осуществляют противофазные колебания с большей из нормальных частот.

В общем случае, при произвольном возбуждении колебаний (например, качнуть один из маятников) каждый из маятников осуществляет сложное колебание, являющееся результатом сложения двух колебаний, происходящих в одном направлении. Если собственные частоты обоих маятников близки, то в результате должны возникнуть биения, которые удобно наблюдать при слабой связи между маятниками, т.е. при выполнении условия (это имеет место при малом расстоянии d). При указанных условиях расстройка - мала по сравнению с нормальными частотами и 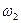. Действительно, если рассмотреть случай когда А = В, то уравнение движения 1-го маятника примет вид (уравнение движения второго маятника рассматривается аналогично):

; (20)

 

преобразовав, получим:

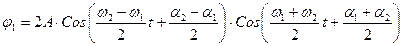(21)

 

Полученное выражение полностью аналогично результату (9) и начальная часть полученного выражения:

(22)

 

будет представлять собой медленно изменяющуюся со временем амплитуду. График такого колебания представлен на рис. 2.

Рис. 3.

Промежуток времени между двумя соседними по времени минимальными или максимальными значениями амплитуды колебаний называют периодом биений (см. рис. 2). Т.к. под амплитудой следует понимать не само выражение (22), а его абсолютную величину т.е.

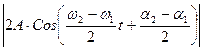, (23)

то, очевидно, что значения амплитуды будут повторяться при изменении аргумента косинуса в (23) на p, т.е. период биений можно определить из условия:

, (24)

учитывая, что

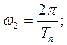
получим

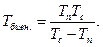(25)

Т.о. видно, что в том случае, когда разность будет малой величиной, а большой и, следовательно, эффект легко наблюдать экспериментально.

Методика выполнения работы

 

1) Т.к. теория связанных колебаний рассмотрена нами для математических маятников, то в начале измерений необходимо убедиться, что физические маятники, используемые в лабораторной установке, близки по своим свойствам к математическим. Для этого нужно измерить время , за которое происходит 10-20 свободных колебаний маятника, и, разделив это время на число колебаний, определить период колебаний. Повторить эту процедуру 3-4 раза. Найти среднее значение периода колебаний . Период колебаний математического маятника, рассчитанный по формуле:

(26)

сравнить со средним значением периода , измеренным экспериментально и рассчитать относительное отклонение экспериментального результата от расчетного значения по формуле:

(27)

Убедиться, что это отклонение не превышает 3-4% и теория математических маятников может, в пределах указанной точности, применяться для используемой экспериментальной установки. Результаты занести в таблицу:

 

 

2) Измерить периоды синфазных и противофазных 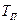колебаний. Для этого измерить время 10-20 колебаний и, разделив на количество колебаний, найти период. Процедуру повторить 3-4 раза и рассчитать среднее значение периодов и .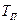

3) Рассчитать период биений по формуле (25), подставив в нее значения периодов и 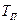, определенные в пункте 2. После этого измерить экспериментально период биений. Для этого измерить 5-6 раз время между двумя последующими остановками маятника и рассчитать среднее значение. Сравнить результат расчета по формуле (25) и результат прямого измерения периода биений.

4) Рассчитать коэффициент жесткости пружинной связи между маятниками. Из формул (16) для определения нормальных частот следует:

 

, .

 

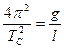Вычитая из второго уравнения первое, можно после несложных преобразований получить:

(28)

 

Величина m обозначена на грузе маятника. Величины l и d можно легко измерить с помощью линейки, а периоды синфазных и противофазных колебаний были определены ранее. Воспользовавшись формулой (28), рассчитать коэффициент жесткости пружины и погрешность, с которой он определен.

Проделать такие измерения дважды при различных положениях пружины, сравнить полученные значения коэффициента жесткости.

Контрольные вопросы:

1) Какие движения называются колебательными?

2) Какие колебания называются гармоническими? Как записывается уравнение гармонических колебаний?

3) Дайте определения и поясните физический смысл параметров гармонических колебаний: амплитуды, периода, частоты, фазы?

4) Что такое связанные колебания? При каких условиях они возникают?

5) Что такое синфазные и противофазные колебания? Как их возбудить?

6) Что такое биения и при каких условиях они возникают?

7) Что называется периодом биений и по какой формуле его можно рассчитать?

 

Литература:

1) Общий физический практикум. Под ред. А.Н. Матвеева и Д.Ф. Киселева., Изд. МГУ, Москва, 1991, 272 с.

2) Физический практикум. Механика и молекулярная физика. Под ред. В.И. Ивероновой. Изд. Наука, Главная ред. Физ.-мат. лит., Москва, 1967, 352 с.

 

 

Приложение 1.

Решим уравнение свободных колебаний (5) и покажем, что решением этого уравнения действительно является гармоническая функция. Решение (5) будем искать в виде e^{l t} (стандартный прием в теории дифференциальных уравнений), где l - некоторая неизвестная пока величина. Тогда

, (29)

 

Подставив (29) в (5), получим:

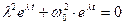(30)

или

(31)

 

Уравнение (31) называется характеристическим уравнением. Из (31) следует:

 

(32)

где - мнимая единица. Т.е. мы выяснили, что l представляет собой мнимое число. Следовательно, частные решения уравнения (4, 5) будут иметь вид:

 

, (33)

 

Из теории дифференциальных уравнений известно, что полное решение однородного дифференциального уравнения представляет собой линейную комбинацию частных решений этого уравнения, поэтому полное решение уравнения (5) будет иметь вид:

(34)

где С₁, и С₂ - некоторые постоянные коэффициенты. Воспользуемся формулами Эйлера, согласно которым

, (35)

Тогда выражение (34) может быть преобразовано к виду:

 

(36)

Сделаем замену, перейдя от неизвестных коэффициентов С₁, С₂ к двум другим величинам a и j, определяемым из соотношений:

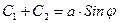, (37)

Тогда, воспользовавшись тригонометрической формулой для синуса сумм двух углов, получим:

(38)

 

Т.о. из полученного результата следует, что координата тела будет изменяться со временем гармонически (т.е. зависимость от времени описываться функциями Sin или Cos):

или

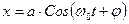
Функции и легко переходят друг в друга при изменении начальной фазы на 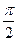, поэтому для определения начальной фазы 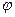следует использовать дополнительные данные, например, начальные или граничные условия.