Использование моста Сотти для экспериментального определения емкости конденсатора и вывод рабочей формулы

ОПРЕДЕЛЕНИЕ ЭЛЕКТРОЕМКОСТИ КОНДЕНСАТОРА

Методические указания к лабораторной работе №8 по физике

 

(Раздел «Электричество»)

 

 

Ростов-на-Дону 2011

 

Составители: Т.П. Жданова, А.Б. Гордеева, И.Г. Попова,

Е.С. Богославская

 

УДК 530.1

 

ОПРЕДЕЛЕНИЕ ЭЛЕКТРОЕМКОСТИ КОНДЕНСАТОРА: метод. указания к лабораторной работе № 8 - Ростов н/Д: Издательский центр ДГТУ, 2011.-9с.

 

Указания содержат краткое описание рабочей установки и методики определения электроемкости конденсатора методом моста Сотти.

Методические указания предназначены для студентов инженерных специальностей всех форм обучения в лабораторном практикуме по физике (раздел «Электричество»).

 

 

Печатается по решению методической комиссии факультета

«Нанотехнологии и композиционные материалы»

 

Научный редактор к.ф.-м.н., доц. Г. Ф. Лемешко

 

© Издательский центр ДГТУ, 2011

 

ОПРЕДЕЛЕНИЕ ЭЛЕКТРОЕМКОСТИ КОНДЕНСАТОРА

Цель работы:

1. Ознакомление с мостовым методом измерения электрической емкости конденсатора.

2. Определение законов сложения емкостей при параллельном и последовательном соединении конденсаторов.

Оборудование: источник переменного тока, магазин эталонных конденсаторов, измеряемые неизвестные конденсаторы, осциллограф, реохорд (реостат, включенный как потенциометр).

 

Теоретическая часть

Если уединенному проводнику сообщить электрический заряд , то потенциал проводника примет некоторое значение 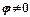, причем , т.е. . Следовательно,

-

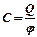электрическая емкость уединенного проводника. Единица ёмкости – фарад (Ф).

Конденсатором называется система из двух близко расположенных проводников (обкладок), разделенных слоем диэлектрика. В зависимости от формы обкладок конденсаторы бывают плоские, цилиндрические и сферические.

Под емкостью конденсатора понимается физическая величина, равная отношению заряда , накопленного в конденсаторе, к разности потенциалов () между его обкладками:

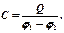
Электроемкость конденсатора зависит от его формы, геометрических размеров и диэлектрической проницаемости среды, заполняющей пространство между обкладками. В случае плоского конденсатора

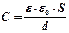, (1)

где =8,85·10^–12 Ф/м – электрическая постоянная; – диэлектрическая проницаемость среды, заполняющей пространство между обкладками; – расстояние между пластинами, - площадь обкладок.

Другой важнейшей характеристикой конденсатора является напряжение пробоя, т.е. минимальная разность потенциалов на обкладках, при которой происходит электрический разряд через слой диэлектрика в конденсаторе. Пробивное напряжение зависит от формы и размеров обкладок и от свойств диэлектрика.

При практическом использовании конденсаторов для получения необходимой емкости собирают батареи из отдельных элементов, соединяя их последовательно или параллельно.

При последовательном соединении конденсаторов заряд на обкладках остается величиной постоянной: 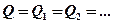, напряжения суммируются:

Тогда электроемкость:

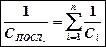. (2)

 

При последовательном соединении на каждый из конденсаторов приходится лишь часть разности потенциалов Δ φ напряжения источника, вследствие чего уменьшается возможность пробоя конденсаторов.

При параллельном соединении конденсаторов напряжение остается величиной постоянной: , заряд батареи конденсаторов: .

Тогда общая электроемкость:

. (3)

Пробивное напряжение такой батареи равно пробивному напряжению того из конденсаторов, у которого оно наименьшее.

 

Использование моста Сотти для экспериментального определения емкости конденсатора и вывод рабочей формулы

 

В данной работе емкость измеряется при помощи мостовой схемы – моста Сотти (рис. 1).

– магазин емкостей (эталонная емкость); – конденсатор, емкость которого надо измерить; источник переменного тока (); индикатор нуля (ИН, в данном случае – осциллограф); реохорд (реостат, включенный как потенциометр); и - плечи реохорда; и 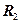- сопротивления плеч и реохорда.

 

Если источник тока включен, то в цепи, в том числе и на участке , течет ток, а на экране осциллографа видна синусоида. Подбором сопротивлений и 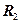(путем перемещения движка реостата) можно добиться равновесия моста, при котором разность потенциалов () равна нулю (состояние равновесия моста), а на экране осциллографа синусоида сменяется горизонтальной прямой. После перехода через положение равновесия амплитуда синусоиды снова увеличивается.

При равновесии моста потенциалы точек и 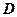равны (). Это значит, что разность потенциалов на участке по величине равна разности потенциалов на участке :

. (4)

По аналогичным соображениям:

. (5)

Токи в ветвях и , и будут равны по величине:

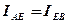, (6)

. (7)

Сопротивление участка цепи переменного тока, содержащего конденсатор, определяется по формуле

, (8)

где – электроемкость конденсатора; ω – циклическая частота.

К однородным участкам цепи АЕ, ЕВ, АD и DВ применим закон Ома в виде:

,

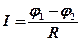тогда равенства (6) и (7) примут вид:

, (9)

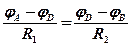. (10)

 

Разделив почленно равенство (9) на (10), учитывая при этом равенства (4), (5) и (8) получим:

. (11)

Поскольку сопротивления плеч потенциометра и пропорциональны их длине, условие равновесия запишется в виде:

, (12)

где - длина реохорда, - длина плеча реохорда.

 

Порядок выполнения работы

 

1. Собрать цепь по схеме, изображенной на рис. 1, подключив конденсатор неизвестной электроёмкости .

2. Включить источник питания и осциллограф, дождаться появления на экране осциллографа синусоиды.

3. На магазине емкостей установить значение емкости 0,5 мкФ. С помощью движка реостата добиться на экране осциллографа прямой линии. Внести значения , , в таблицу 1.

4. По формуле (12) вычислить . Результаты занести в таблицу 1.

5. Повторить пункты 1-4 для = 2,0; 4,0 мкФ. Записать значения , , и в таблицу 1.

6. Повторить п. 1-5 для конденсатора неизвестной электроёмкости .

7. Рассчитать средние значения неизвестных емкостей, абсолютную и относительную погрешности измерений и занести в таблицу 1.

8. Соединить измеренные конденсаторы и последовательно и повторить пункты 1-5. Записать значения , , в таблицу 2.

9. Рассчитать по формуле (12) . Результаты занести в таблицу 2.

 

10. Найти общую электроемкость при последовательном соединении по формуле (2) для средних значений и .

11. Оценить относительную погрешность:

(13)

12. Соединить измеренные конденсаторы и параллельно и измерить их общую емкость по пунктам 1-5. Записать значения , , в таблицу 2.

13. Рассчитать по формуле (12) 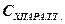. Результаты занести в таблицу 2.

14. Найти общую электроемкость при параллельном соединении по формуле (3) для средних значений и .

15. Оценить относительную погрешность по формуле (13)

 

 

Таблица 1.

 

№
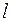
[ ]	мм	мм	мкФ	мкФ	мкФ	%
Емкость первого конденсатора :
ср
Емкость второго конденсатора :
ср

 

 

Таблица 2.

 

№
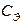
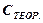
[ ]	мм	мм	мкФ	мкФ	мкФ	%	мкФ	%
При последовательном соединении и :
ср
При параллельном соединении и :
ср

Контрольные вопросы

 

1. Что называется электроемкостью уединенного проводника? От чего она зависит?

2. В каких единицах измеряется электроемкость?

3. Что представляет собой конденсатор?

4. Опишите устройство и принцип действия моста Сотти.

5. Три одинаковых конденсатора один раз соединены последовательно, другой – параллельно. Во сколько раз и когда электроемкость батареи будет больше?

6. Написать формулу электроемкости плоского конденсатора.

7. Как определить общую электроемкость при параллельном и последовательном соединении?

8. Какой радиус должен иметь проводящий шар, чтобы в вакууме его емкость равнялась 1 Ф?

10. Можно ли, имея два одинаковых конденсатора, получить емкость вдвое меньшую и вдвое большую, чем у одного из них? Если можно, то, как это сделать?

 

Рекомендуемая литература

 

1. Трофимова Т. И. Курс физики.- М.: Высш. шк., 2004

2. Электростатика. Постоянный электрический ток: учеб. пособие. /B.C. Кунаков, И.В. Мардасова, О.М. Холодова, В.А. Тызыхян. – Ростов н/Д: Издательский центр ДГТУ, 2010. – 66 с.

3. Яворский Б. М., Детлаф А. А. Справочник по физике.-М.:Наука, 2006

4. Калашников С.Г. 6-е изд., стереот. - М.: ФИЗМАТЛИТ, 2003.- 624 с.

 

Редактор А.А.Литвинова

В печать

Объём 0,7 усл.п.л. Офсет. Формат 60х84/16.

Бумага тип №3. Заказ №. Тираж 50 экз. Цена

Издательский центр ДГТУ

Адрес университета и полиграфического предприятия:

344010, г.Ростов-на-Дону, пл.Гагарина,1.