Подготовка к контрольной работе по теме «Производная и дифференциал».
Теоретический материал.
| Производная | |||
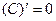 (C–const) (C–const)
| 
| ||

| 
| ||

| 
| ||

| 
| ||

| 
| ||

| 
| ||

| 
| ||

| 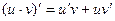
| ||

| 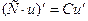
| ||

| 
|
Дифференцирование неявных функций.
Чтобы найти производную функции 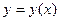 (или
(или  ), которая неявно задана соотношением F(x,y)=0, дифференцируем обе части равенства по независимой переменной x (или y), считая другую переменную функцией от неё, применяя формулу дифференцирования сложной функции. В результате получаем уравнение относительно искомой производной, разрешая его, получаем производную в неявной форме.
), которая неявно задана соотношением F(x,y)=0, дифференцируем обе части равенства по независимой переменной x (или y), считая другую переменную функцией от неё, применяя формулу дифференцирования сложной функции. В результате получаем уравнение относительно искомой производной, разрешая его, получаем производную в неявной форме.
Прием логарифмического дифференцирования.  .
.
1.  .
.
2.  .
.
3.  .
.
Дифференцирование параметрических функций

 , т.е.
, т.е. 
 .
.
Уравнение касательной к кривой  в точке
в точке  :
: 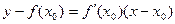 .
.
Уравнение (соответствующей) нормали:  .
.
Производные и дифференциалы высших порядков.
 .
.  .
.
 .
. 
 .
.
Примеры.
Пример 1.  .
.
Пример 2. Правило дифференцирования сложной функции:  .
.
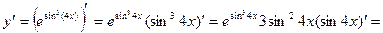
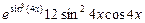 .
.
Пример 3. Найти производную  неявно заданной функции
неявно заданной функции  .
.
Дифференцируем равенство, считая, что x - независимая переменная, а у функция от х: 

 . Раскроем скобки, оставим в правой части слагаемые, содержащие
. Раскроем скобки, оставим в правой части слагаемые, содержащие  :
:  . Выразим из этого уравнения искомую производную:
. Выразим из этого уравнения искомую производную:  или
или  .
.
Пример 4.Найти производную функции.
Прологарифмируем функцию:  . Дифференцируем обе части равенства по x:
. Дифференцируем обе части равенства по x:  . Из этого уравнения находим:
. Из этого уравнения находим: 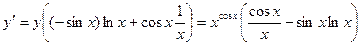 .
.
Пример 5. Найти производные 1-го и 2-го порядка циклоиды  .
.

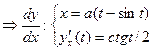 . Аналогично:
. Аналогично:  .
.
Пример 6. Составить уравнения касательной и нормали к кривой  в точке
в точке  .
.
Находим:  ,
, 
 - уравнение нормали.
- уравнение нормали.
Пример 7. Найти производную и дифференциал 3-го порядка функции  .
.
Находим: 
 .
.
№1
1. Найти производные функций: а)  ,
б) ,
б)  , в) , в)  , г) , г)  ,
д) ,
д)  2. Составить уравнения касательной и нормали к кривой
2. Составить уравнения касательной и нормали к кривой 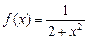 в точке в точке  .
3. Найти дифференциал 2–го порядка .
3. Найти дифференциал 2–го порядка 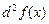 , если , если  . .
| №2
1. Найти производные функций: а) 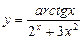 ,
б) ,
б)  , в) , в)  ,
г) ,
г)  , д) , д)  2. Составить уравнения касательной и нормали к кривой
2. Составить уравнения касательной и нормали к кривой 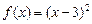 в точке в точке  .
3. Найти дифференциал 2–го порядка .
3. Найти дифференциал 2–го порядка 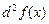 , если , если 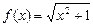 . .
|
№3
1. Найти производные функций: а)  , б) , б)  , в) , в)  , г) , г)  , д) , д)  2. Составить уравнения касательной и нормали к кривой
2. Составить уравнения касательной и нормали к кривой 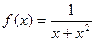 в точке в точке  .
3. Найти дифференциал 2–го порядка .
3. Найти дифференциал 2–го порядка  , если , если  . .
| №4
1. Найти производные функций: а)  ,
б) ,
б)  , в) , в) 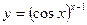 ,
г) ,
г)  , д) , д)  2. Составить уравнения касательной и нормали к кривой
2. Составить уравнения касательной и нормали к кривой  в точке в точке  .
3. Найти дифференциал 2–го порядка .
3. Найти дифференциал 2–го порядка  , если , если  . .
|
№5
1. Найти производные функций: а) 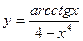 ,
б) ,
б)  , в) , в)  ,
г) ,
г)  , д) , д)  .
2. Составить уравнения касательной и нормали к кривой .
2. Составить уравнения касательной и нормали к кривой  в точке в точке  .
3. Найти дифференциал 2–го порядка .
3. Найти дифференциал 2–го порядка  , если , если 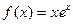 . .
| №6
1. Найти производные функций: а)  ,
б) ,
б) 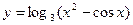 , в) , в)  ,
г) ,
г)  , д) , д) 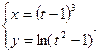 2. Составить уравнения касательной и нормали к кривой
2. Составить уравнения касательной и нормали к кривой  в точке в точке  .
3. Найти дифференциал 2–го порядка .
3. Найти дифференциал 2–го порядка  , если , если  . .
|
№7
1. Найти производные функций: а)  ,
б) ,
б)  , в) , в)  ,
г) ,
г)  , д) , д)  2. Составить уравнения касательной и нормали к кривой
2. Составить уравнения касательной и нормали к кривой 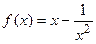 в точке в точке  .
3. Найти дифференциал 2–го порядка .
3. Найти дифференциал 2–го порядка  , если , если 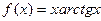 . .
| №8
1. Найти производные функций: а)  ,
б) ,
б)  , в) , в)  ,
г) ,
г)  , д) , д)  2. Составить уравнения касательной и нормали к кривой
2. Составить уравнения касательной и нормали к кривой  в точке в точке  .
3. Найти дифференциал 2–го порядка .
3. Найти дифференциал 2–го порядка  , если , если  . .
|
№9
1. Найти производные функций: а)  ,
б) ,
б) 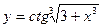 , в) , в)  , г) , г)  ,
д) ,
д)  2. Составить уравнения касательной и нормали к кривой
2. Составить уравнения касательной и нормали к кривой 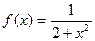 в точке в точке  .
3. Найти дифференциал 2–го порядка .
3. Найти дифференциал 2–го порядка  , если , если  . .
| №10
1. Найти производные функций: а)  ,
б) ,
б) 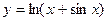 , в) , в)  ,
г) ,
г)  , д) , д)  2. Составить уравнения касательной и нормали к кривой
2. Составить уравнения касательной и нормали к кривой  в точке в точке  .
3. Найти дифференциал 2–го порядка .
3. Найти дифференциал 2–го порядка  , если , если  . .
|
№11
1. Найти производные функций: а)  , б) , б)  , в) , в)  , г) , г)  , д) , д)  2. Составить уравнения касательной и нормали к кривой
2. Составить уравнения касательной и нормали к кривой 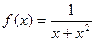 в точке в точке  .
3. Найти дифференциал 2–го порядка .
3. Найти дифференциал 2–го порядка  , если , если  . .
| №12
1. Найти производные функций: а)  ,
б) ,
б)  , в) , в) 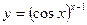 ,
г) ,
г)  , д) , д)  2. Составить уравнения касательной и нормали к кривой
2. Составить уравнения касательной и нормали к кривой  в точке в точке  .
3. Найти дифференциал 2–го порядка .
3. Найти дифференциал 2–го порядка  , если , если  . .
|
№13
1. Найти производные функций: а) 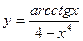 ,
б) ,
б)  , в) , в)  ,
г) ,
г)  , д) , д)  .
2. Составить уравнения касательной и нормали к кривой .
2. Составить уравнения касательной и нормали к кривой  в точке в точке  .
3. Найти дифференциал 2–го порядка .
3. Найти дифференциал 2–го порядка  , если , если 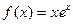 . .
| №14
1. Найти производные функций: а)  ,
б) ,
б) 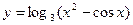 , в) , в)  ,
г) ,
г)  , д) , д) 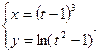 2. Составить уравнения касательной и нормали к кривой
2. Составить уравнения касательной и нормали к кривой  в точке в точке  .
3. Найти дифференциал 2–го порядка .
3. Найти дифференциал 2–го порядка  , если , если  . .
|
№15
1. Найти производные функций: а)  ,
б) ,
б)  , в) , в)  ,
г) ,
г)  , д) , д)  2. Составить уравнения касательной и нормали к кривой
2. Составить уравнения касательной и нормали к кривой  в точке в точке  .
3. Найти дифференциал 2–го порядка .
3. Найти дифференциал 2–го порядка  , если , если 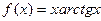 . .
| №16
1. Найти производные функций: а)  ,
б) ,
б) 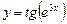 , в) , в)  ,
г) ,
г)  , д) , д)  2. Составить уравнения касательной и нормали к кривой
2. Составить уравнения касательной и нормали к кривой 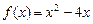 в точке в точке  .
3. Найти дифференциал 2–го порядка .
3. Найти дифференциал 2–го порядка  , если. , если. 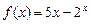 . .
|
№17
1. Найти производные функций: а)  ,
б) ,
б)  , в) , в) 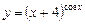 , г) , г)  ,
д) ,
д)  2. Составить уравнения касательной и нормали к кривой
2. Составить уравнения касательной и нормали к кривой  в точке в точке  .
3. Найти дифференциал 2–го порядка .
3. Найти дифференциал 2–го порядка  , если , если  . .
| №18
1. Найти производные функций: а)  ,
б) ,
б)  , в) , в)  ,
г) ,
г)  , д) , д)  2. Составить уравнения касательной и нормали к кривой
2. Составить уравнения касательной и нормали к кривой  в точке в точке 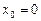 .
3. Найти дифференциал 2–го порядка .
3. Найти дифференциал 2–го порядка  , если , если  . .
|






