Примерный перечень экзаменационных вопросов

Методы координат на плоскости.
Основные задачи, решаемые методом координат.
Уравнение прямой с угловым коэффициентом.
Общее уравнение прямой.
Уравнение прямой, проходящей через данную точку с данным угловым коэффициентом.
Уравнение прямой, проходящей через две данные точки.
Уравнение прямой в отрезках.
Угол между двумя прямыми.
Взаимное расположение двух прямых на плоскости.
Расстояние от точки до прямой.
Уравнение окружности.
Каноническое уравнение эллипса.
Каноническое уравнение гиперболы.
Директрисы эллипса и гиперболы.
Каноническое уравнение параболы.
Матрица. Виды матриц.
Операции над матрицами.
Определители квадратных матриц.
Миноры, алгебраические дополнения, теорема Лапласа.
Обратная матрица. Алгоритм вычисления обратной матрицы.
Ранг матрицы.
Решение системы линейных уравнений (СЛАУ) по формулам Крамера.
Решение СЛАУ методом обратной матрицы.
Решение СЛАУ методом Гаусса.
Теорема Кронекера – Капелли.
Дать основные понятия вектора.
Линейные операции над векторами.
Понятие линейной зависимости векторов.
Линейная зависимость векторов на плоскости.
Линейная зависимость векторов в пространстве.
Базис на плоскости и в пространстве.
Скалярное произведение векторов и его основные свойства.
Направляющие косинусы вектора.
Векторное произведение векторов и его основные свойства.
Смешанное произведение векторов и его основные свойства.
Плоскость. Уравнение плоскости, проходящей через данную точку перпендикулярно к данному вектору.
Неполное уравнение плоскости.
Уравнение плоскости в отрезках.
Расстояние от точки до плоскости.
Угол между плоскостями.
Условия параллельности и перпендикулярности плоскостей.
Общее уравнение прямой в пространстве.
Каноническое уравнение прямой в пространстве.
Параметрические уравнения прямой.
Уравнение прямой в пространстве, проходящее через две различные данные точки.
Угол между прямыми в пространстве.
Условия параллельности и перпендикулярности прямой и плоскости.
Уравнение плоскости, проходящей через данную точку и параллельной данной плоскости.
Уравнение плоскости, проходящей через две данные точки перпендикулярной к данной плоскости.
Уравнение плоскости, проходящей через три данные точки не лежащие на одной прямой.

Задание 1. Найти указанные пределы (не используя правило Лопиталя).

а). ; б). ;

в). ; г). ; д). .

Решение.

а). . Непосредственная подстановкапредельного значения аргумента х=3приводит к неопределенности вида . Чтобы раскрыть эту неопределенность разложим числитель и знаменатель на множители по формуле аx² + bx + c = а(x – x₁)(x – x₂), где х₁ и х₂ – корни квадратного трехчлена, и сократим члены дроби на общий множитель (х – 3). Так как аргумент х только стремится к своему предельному значению 3, но не совпадает с ним, то множитель (х – 3) отличен от нуля при х 3. Будем иметь: .

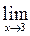
б). . При х имеем неопределенность вида . Разделим числитель и знаменатель дроби на х² (х² 0 при х ). Получим: = = (по свойствам пределов).

в). [¥ - ¥] =

г). . Непосредственная подстановка х=0дает неопределенность вида . Умножимчислитель и знаменатель дроби на выражение . Имеем:

= = .

д). . При х основание стремится к I, показатель степени 7х+3 стремится к ¥. Следовательно имеем неопределенность вида [ ]. Используем второй замечательный предел . Представим основание в виде суммы I и некоторой бесконечной малой величины . Тогда = =

= .

f(x) = , x = 0.

Задание 2.

Функция y=f(x) задана различными аналитическими выражениями для различных областей изменения независимой переменной. Найти точки разрыва функции, если они существуют. Построить график функции:

Решение.

Функции у = х² + 1, у = 2, у = 3х непрерывны на всей числовой прямой, поэтому данная функция может иметь разрывы только в точках, где меняется ее аналитическое выражение, т.е. в точках х₁= 1 и х₂= 2.

Исследуем функцию на непрерывность в этих точках, для чего найдем соответствующие односторонние пределы и значения функции.

В точке х₁ = 1 имеем:

, ,

а значение не определено. Отсюда следует, что х₁ = 1 – точка устранимого разрыва. Для точки х₂= 2 получим:

, ,

Таким образом, в этой точке ,

т.е. функция имеет разрыв 1-го рода.

Таблица производных простейших элементарных функций

Значения производных от основных элементарных функций c независимым аргументом х и со сложным аргументом u.

1. (xⁿ) ′ = n x^{n – 1} (uⁿ) ′_x = n u^{n – 1} u′_x

2. ()′ = ()′_x =

3. = _x =

4. (e^x) ′ = e^x(e^u) ′_x = e^u u′_x

5. (a^x) ′ = a^x lna (a^u) ′_x = a^u ln a u′_x

6. (ln x) ′ = (ln u) ′_x =

7. (log_a x) ′ = (log_a u)_x =

8. (sin x) ′ = cos x (sin x) ′_x = cos u u′_x

9. (cos x) ′ = - sin x (cos x) ′_x = - sin u u′_x

10. (tg x) ′ = (tg u) ′_x =

11. (ctg x)` = (ctg u) ′_x =

12. ( arcsin x) ′ = (arcsin u)`_x =

13. ( arcсos x) ′ = (arccos u) ′_x =

14. (arctg x) ′ = (arctg u) ′_x =

15. (arcctg x) ′ = (arcctg u) ′_x =

Задание 3. Найти производные функций:

а) ; б) у= ; в) ;

г) y = x^x; д) е^у+ е^-х+ ху =0.

Решение.

а) Используя правило дифференцирования дроби, получим:

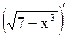. Вычислим далее производные каждого из выражений и : =6х + 1; = . Будем иметь: .

б) Воспользуемся вначале правилом дифференцирования сложной степенной функции:

. Найдем далее производную разности . Производная выражения есть производная сложной показательной функции. Она равна: .

Производная выражения есть производная сложной логарифмической функции. Она равна: .Окончательно будем иметь: . .

в) Предварительно преобразуем функцию, используя свойство логарифмов: . Применяя правила дифференцирования разности функций и сложной логарифмической функции, получим: .

г) Предварительно прологарифмируем по основанию е обе части равенства ln y = x ln x. Теперь дифференцируем обе части, считая ln y сложной функцией от переменной х: (ln y) ′ = = ln x + . Окончательно имеем:

y′ = y [ ln x + 1 ] = = x^x [ ln x + 1 ].

д) При дифференцировании неявно заданной функции учитываем, что у есть функция от х, получим: е^у∙ у′ - е^-х+ у + ху′ =0, откуда .

Задание 5.

Исследовать методами дифференциального исчисления и построить график

функции:

- кусочно – непрерывная функция.

Решение.

1) D(f) = (0,1) (1,+ ), х = 1 - точка разрыва.

2) Функция не является ни четной, ни нечетной.

3) Находим асимптоты графика функции.

, т.е. х = 1 - вертикальная асимптота.

Наклонной и горизонтальной асимптоты нет, т.к. , .

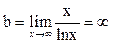4) Находим интервалы возрастания и убывания функции и ее экстремумы.

Условие дает ln x–1= 0 или x = e - подозрительную на экстремум точку, которая вместе с точкой разрыва делит D(f) на 3 интервала монотонности. Составим таблицу, где определим знаки f′ (x) и направление монотонности для каждого интервала

x	(0,1)	(1,e)	e	(e,+ )
y			min
y′	-	-		+

на (0, 1) y′(e^-1) = - 2 < 0 y - убывает;

на (1, e) y′(e^1/2) = -2 < 0 y - убывает;

на (e, + ) y′(e²) =1/2 > 0 y – возрастает.

5) Находим интервалы выпуклости и вогнутости и точки ее перегиба.

Условие y′′ = (-ln x + 2)/ x ln³ x = 0 дает ln x = 2 или x = e² подозрительную на перегиб точку, которая вместе с точкой разрыва разделяют D(f) на 3 интервала монотонности. Составим таблицу, где определим знак f′′(x) и направление выпуклости для каждого интервала.

x	(0,1)	(1,e)	e²	(e²,+ )
y			т.п. e²/2
y′′	-	+		-

на (0, 1) y ′′(1/ e) = -3e < 0 y - выпукла вверх;

на (1, e²) y ′′(e) = e^-1> 0 y - выпукла вниз;

на (e²,+ ) y ′′(e³) = -1/27e^-3 < 0 y - выпукла вверх.

6) Точек пересечения с осями координат нет.

7) Значения функции в граничных точках:

; ; ;

8) Строим график функции