второе можно назвать драгоценным камнем.
Иоганн Кеплер (ХV1в.)
В потоке времён и событий сверкающие грани драгоценного камня Sectio divina – Божественного сечения – высвечивают посвященным наиболее сокровенные черты Божественного устройства мира и гармонии жизни.История познания Божественного сечения уходит в глубь тысячелетий. Принцип Божественных соотношений или пропорций дан Богом человеку еще в раю, а затем праотцу Ною при постройке ковчега спасения.
Впервые сведения о Божественном сечении встречаются в “Началах” Евклида /3в.доРХ/ в виде задачи деления отрезка в среднем и крайнем отношении. Иначе, отрезок прямо делится на две неравные части таким образом, что большая часть его становится средним пропорциональным между целым отрезком и его меньшей частью.
А = 0,618 В = 0,382
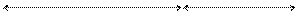
1
Математическое выражение этого соотношения таково:
(А+В): А = А: В
Если за целое принять 1, получится система уравнений, решив которую, можно найти золотое число:
А + В = 1 В = 1 – А
(А + В):А = А:В 1:А = А:(1 – А) 1/А=А/1-А А2 = 1 – А
А = (-1 + Ö (1 + 4)): 2 отрезок делится А = 0,618
В = 1 - А на такие части: В = 0,382
Общепринятым обозначением этой пропорции является буква Ф – первая буква имени Фидия, знаменитого скульптора Древней Греции, применявшего Божественное сечение в своих произведениях. Ф – иррациональное число, которым выражается пропорциональное соотношение между целым и его частями:
Ф = 1, 618033988749…
Число Ф с точностью до третьего знака равно 1,618. Если из числа Ф вычесть 1, то получится 0,618. Однако, если 1 поделить на 0,618, то получится снова число Ф = 1,618:
1,618 – 1 = 0,618
1: 0,618 = 1,618
Т.е данная пропорция обладает аддитивными и мультипликативными свойствами.
Закон Божественного сечения
 |
Этот принцип можно сформулировать и по-другому: как большее относится к меньшему, так и целое относится к большему. Или: как меньшее относится к большему, так и большее относится к целому.
Золотоесечение можно найти графическим путем – с помощью циркуля и линейки.
 |
R1
R2-золотое сечение
R1
R2 R1=половине отрезка
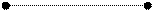
4
Середина отрезка
Название Божественная пропорция / ит. De divina proportione / происходит от итальянского математика Луки Пачиоли, издавшего в 1509 году книгу одноименного названия. Книга иллюстрирована великим Леонардо да Винчи, которому принадлежит название «золотое сечение» / ит. Sectio aurea/.
Однако, ещё в 13 веке, итальянский математик Леонардо Фибоначчи открыл ряд чисел, впоследствии названный рядом Фибоначчи.
0 – 1 – 1 – 2 – 3 – 5 – 8 – 13 – 21 – 34 – 55 – 89 – 144 – 233 – 377 …
Суть его гениально проста: каждый последующий член этого ряда равен сумме двух предыдущих:
0+1=1, 1+1=2, 1+2=3, 2+3=5, 3+5=8, 5+8=13, 8+13=21...
А отношение двух соседних чисел приближается к величине золотого сечения (Ф=1,618…) особенно по мере увеличения чисел:
5:3=1,666; 13:8=1,625; 34:21=1,619; 144:89=1,618…
Можно сказать, что чем больше соседние члены ряда стремятся в бесконечность, тем их отношение ближе к Божественному сечению!
· Если этот принцип применить к человеку, то можно сказать, что чем больше, шире душа человека, тем ближе он к миру Божественных законов, Божественных заповедей.
· Интересно, что 10 Божественных заповедей можно рассматривать также в соотношении золотого сечения: они разделяются на 4 и 6. Первые касаются отношений человека и Бога, остальные 6 заповедей определяют человеческие взаимоотношения.
· С помощью ряда Фибоначчи можно быстро решать задачи гармонического построения любой формы и организации любого пространства. Яркий пример тому – создание Божественно устроенных сооружений, которые описываются в Ветхом Завете (см.выше). Так скиния Моисеева зиждется на соотношении: 1, 1, 3, 5, а пропорции Храма Соломонова основаны на числах: 1, 2, 3. Сравните с удивительным рядом Фибоначчи.
СИСТЕМА «ДВУХ КВАДРАТОВ» (26)
Если начертить рядом два одинаковых квадрата, то получится прямоугольник со сторонами 1:2. Затем проведем диагональ в прямоугольнике и окружность с радиусом, равным диагонали /см. рис./.
| |||||
  | |||||
 | |||||
2
Любую архитектурную деталь и всё сооружение в целом можно вписать или в квадрат, или в прямоугольник. Его стороны могут относиться разным образом, но величинами, присутствующими в данном чертеже. Всё полученное множество прямоугольников гармонически сочетается друг с другом – это и есть главное качество системы двух квадратов.
Приглашаем боголюбивого читателя
к исследованию тайн Божественных пропорций,
чтобы соприкоснуться с миром Красоты Божественной Гармонии
и воздать хвалу ея Творцу.
ДРЕВНЕРУССКИЙ ВСЕМЕР
Система размеров и их отношений в древнерусской архитектуре (18)
Творческий метод древнерусских зодчих далеко не во всем нам понятен, и многое остается для нас загадкой. Однако, анализ форм произведений древнерусской архитектуры показывает, что их красота при своей простоте обладает пропорциями весьма непростыми, лучшими из известных нам видов – золотым сечением и различными производными от него функциями.
Методы работы древнерусских зодчих поражают нас – в короткие сроки возводились сложнейшие здания без чертежей! Древнерусские мастера владели определенной спецификой проектирования, знаниями и умениями, которые неведомы для нас…
Сравним для примера некоторые размеры шедевров древнего зодчества:
- толщина стен Коломенского Кремля = 3,72; 4,6; 4,88 м.
- высота стен Тульского Кремля = 3,7; 4,6 м.
- в митрополичьих покоях размер кельи 4,61 х 4,61 м и т.д.
Размеры не просто совпадают. Раньше случайных размеров не применяли! В данных примерах исходные величины – это сажени размерами 186,4; 230,4; 244 и 197,4 см.
· Сажень 186,4 см – «церковная» или «трубная». Она равна 2,5 аршина и 2 вершка, что составляет 42 вершка (при вершке 4,445 см): 4,445 х 42 = 186,7 см.
Церковная сажень совпадает с римским пассом.
· Сажень 230,4 см – «греческая». Происходит от греческой оргии, размер которой состаавлет 231,1 (или 231,9)см. Эта сажень широко применялась, но не для бытовых сооружений, а для проектирования произведений архитектуры и искусства.
· Сажень 244 см – великая.
· Сажень 197,4 см – царская.
Одновременное применение нескольких видов саженей в одном сооружении – символически осмысленно и позволяло гармонически проектировать сооружения.
Другая группа саженей:
· Сажень 176 см – «народная», «лавочная», «мерная». Она мерилась размахом рук человека среднего и выше среднего роста. Применялась соответственно названию – напр., длина помещения казны в Воскресенской церкви в Крутицах равна 10,55 м, что составляет 6 лавочных саженей.
· Сажень 142,4 см – «малая». Часто использовалась. (Равна удвоенному шагу?)
· Сажень 150,8 см – «простая».
· Сажень 217,6 см – «казенная». Редко применялась.
· Сажени 134,5 и 159,7 и др. – «кладочные». Применялись для составления размеров кирпичной кладки в простенках и столбах.
Красной нитью сквозь все древние творения зодчих проходит поразительный закон: величины системы размеров и их отношений в древнерусской архитектуре разработаны на основе модели человека! (Подробнее об этом см. ниже).
Рассмотрим систему величин пропорционирования с дополнением двухрядной модулярной схемы новыми рядами Фибоначчи:
24 40
12 20 32 52
6 10 16 26 42
3 5 8 13 21 34 55
1,5 2,5 4 6,5 10,5 17 27,5 44,5
0,75 1,25 2 3,25 5,25 8,25 13,75 22,25 36 58,25
Все горизонтальные линии являются одиночными рядами Фибоначчи. Отношение двух соседних величин приближается к золотому сечению по мере удаления от начала ряда. По вертикали – удвоение величин вверх, а вниз – деление на половину. Каждая пар рядов обладает комбинаторикой модулора Корбюзье, а весь комплекс величин – еще более высокими комбинаторными свойствами.
В этой системе присутствуют величины всех древнерусских саженей. Если выписать в один ряд величины, завершающие вертикальные столбцы схемы, в порядке слева направо, то получится такой числовой ряд:
48 40 32 52 42 34 55 44,5 36 58,25
Напомним древнерусские сажени и разместим их в следующем порядке:
217,6176 142,4230,4 186,4150,8244 197,4159,7258,4
49 39,5 32 52 42 34 55 44,5 36 58,25
В верхнем ряду даны размеры саженей в сантиметрах; в нижнем – это размеры в вершках с округлением до ¼ вершка (1 вершок = 4,445см).
Выраженные в вершках размеры древнерусских саженей и их соподчиненные единицы совпадают с величинами рассмотренной схемы.
Примечания
· Небольшие отклонения происходят лишь в начале ряда, в двух первых членах. Это напоминает отклонения от золотого сечения в соотношениях начальных членов ряда Фибоначчи.
· Несколько видоизменено расположение величин, которые приводятся в сантиметрах. Все отношения величин уточнены по золотому сечению, и поэтому отношения начальных членов столь же «золотые», как и последующих.
· Вверху даются размеры древнерусских саженей. Они являются основными и исходными. Под каждой из них расположены их половинные, четвертные, восьмые и т. д. доли, слагающие систему 1—2—4—8...
Каждая вертикаль представляет собой систему величин одной сажени – особенность, на которую обратил внимание Б.Л.Рыбаков. он писал: «Одним из существенных отличий русской народной метрологии от древнегреческой, римской или византийской и западноевропейской метрологии является принцип постепенного деления на 2, когда меньшие меры получаются путем деления большей на 2, на 4 и на 8... Полусажень; локоть, представляющий четвертую часть сажени; четверть или четь, под которыми мы должны понимать четвертую часть полусажени; пядь – вот доли основной меры сажени».
В основе системы древнерусских мер лежит вышеприведенная схема. Ниже представлена более полно система древнерусских мер, т.н. древнерусский всемер.
ДРЕВНЕРУССКИЙ ВСЕМЕР
(величины в вершках, 1 вершок = 4,445 см)
24 – 40
12 – 20 – 32 – 52
6 – 10 – 16 – 26 – 42
3 – 5 – 8 – 13 – 21 – 34 – 55 (РЯД ФИБОНАЧЧИ)
1,5 – 2,5 – 4 – 6,5 – 10,5 – 17 – 27,5 – 44,5
0,75 – 1,25 – 2 – 3,25 – 5,25 – 8,5 – 13,75 – 22,25 – 36
СВОЙСТВА РЯДА ФИБОНАЧЧИ (1 – 2 – 3 – 5 – 8 – 13 – 21 – 34 – 55)
1+2=3 2+3=5 3+5=8 5+8=13 …
2:1=2 3:2=1,5 8:5=1,6 … 34:21=6,619 (ЗОЛОТОЕ СЕЧ.=1,618…)
