Виды модуляции
Для переноса спектра частот первичного сигнала в требуемую частотную область, например в область пропускания канала связи, используют модуляцию.
Процесс модуляции заключается в изменении какого-либо одного или нескольких параметров переносчика информации (амплитуды, частоты, фазы, синусоидального колебания или импульсов) в соответствии с передаваемым сообщением.
Модулирующий (информационный) сигнал воздействует на тот или иной параметр переносчика информации, изменяя его таким образом, чтобы он полностью отражал информационную сущность модулирующего сигнала.
Следовательно, при модуляции воздействие модулирующего (информационного) сигнала 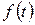 взаимодействует с переносчиком
взаимодействует с переносчиком 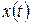 ,который подается в преобразователь (модулятор) от специального генератора. Как правило, переносчик представляет собой детерминированное периодическое колебание, характеризуемое
,который подается в преобразователь (модулятор) от специального генератора. Как правило, переносчик представляет собой детерминированное периодическое колебание, характеризуемое 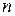 параметрами, и может быть представлено функцией времени
параметрами, и может быть представлено функцией времени 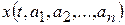 , где
, где 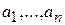 — параметры переносчика.
— параметры переносчика.
Гармонические и импульсные сигналы, соответственно, описываются выражениями:
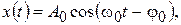
где 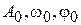 — амплитуда, угловая частота и начальная фаза гармонического колебания;
— амплитуда, угловая частота и начальная фаза гармонического колебания;
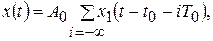
где 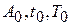 — амплитуда (высота), начальная фаза (сдвиг относительно выбранного начала отсчета) и период следования импульсов
— амплитуда (высота), начальная фаза (сдвиг относительно выбранного начала отсчета) и период следования импульсов 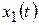 .
.
В качестве носителей могут использоваться и шумовые сигналы, представляющие собой случайный процесс. Параметрами переносчика в этом случае служат их числовые характеристики.
В результате модуляции на выходе преобразователя (модулятора) получают модулированный сигнал 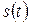 , представляющий собой отклик
, представляющий собой отклик 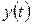 преобразователя на воздействие
преобразователя на воздействие 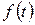 :
:
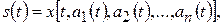
где 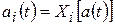 —
— 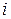 -й модулированный параметр (здесь
-й модулированный параметр (здесь 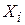 — оператор преобразования
— оператор преобразования 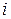 -го параметра).
-го параметра).
Каждый модулированный параметр изменяется в соответствии с воздействием модулирующего (информационного) сигнала 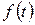 . Оператор преобразования модулированного параметра
. Оператор преобразования модулированного параметра
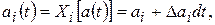
где 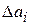 — девиация
— девиация 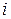 -го параметра. Данное выражение справедливо для большинства гармонических и импульсных видов модуляции по одному параметру.
-го параметра. Данное выражение справедливо для большинства гармонических и импульсных видов модуляции по одному параметру.
Следовательно, осуществляющий модуляцию преобразователь (модулятор) должен представлять собой четырехполюсник с переменными параметрами. Как правило, модуляция сопровождается преобразованием частотного спектра и динамического диапазона.
Носитель информации называют также несущим колебанием или несущей частотой, в соответствии, с чем различают гармоническую и импульсную модуляции.
При гармонической модуляции несущими (модулируемыми) являются гармонические колебания. В зависимости от модулируемого параметра различают амплитудную (AM), частотную (ЧМ) и фазовую (ФМ) модуляции.
При импульсной модуляции в качестве несущих используют последовательность импульсов. В этом случае в зависимости от модулируемого параметра, различают амплитудно-импульсную модуляцию (АИМ), длительно-импульсную (широтно-импульсную) модуляцию (ДИМ/ШИМ)), временно-импульсную модуляцию (ВИМ), разновидностями которой являются фазо (ФИМ) и частотно-импульсная (ЧИМ) модуляции.
К сложным видам импульсной модуляции относятся дельта-модуляция (ДМ) и импульсно-кодовая модуляция (ИКМ). Частным случаем модуляции является манипуляция сигналов, при котором в качестве модулирующего (информационного) сигнала используется последовательность одно- или двухполярных прямоугольных импульсов. Используют ее в системах передачи дискретной информации.
Иногда необходимо осуществить изменение нескольких параметров несущего колебания, т. е. смешанную модуляцию. Например, можно выполнить амплитудно-частотную и амплитудно-фазовую модуляции гармонического колебаний несущей. При этом в случае многоканальной передачи на различные параметры несущей могут воздействовать разные модулирующие (информационные) сигналы.
При необходимости можно осуществить поэтапную (многоступенчатую) модуляцию: ЧМ — AM, AM — ЧМ, AM — AM, АИМ — AM, ДИМ — ФМ и т. д. Так, при AM — ЧМ первоначально исходный информационный сигнал модулирует поднесущее колебание по амплитуде, а затем АМ-колебание модулирует основной носитель по частоте. Многоступенчатая модуляция используется для более качественного согласования источника информации с параметрами канала, позволяющего получить более высокую помехоустойчивость передачи информации.
Амплитудная модуляция
Колебания носителя гармонических видов модуляции можно представить в следующем виде:
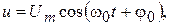
где 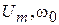 и
и 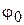 — соответственно постоянные амплитуда, круговая частота и начальная фаза гармонического колебания.
— соответственно постоянные амплитуда, круговая частота и начальная фаза гармонического колебания.
Модулирующую функцию, т. е. закон изменения информационного сигнала обозначают 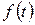 . При амплитудной модуляции модулирующий сигнал
. При амплитудной модуляции модулирующий сигнал 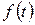 воздействует на постоянную амплитуду колебаний переносчика
воздействует на постоянную амплитуду колебаний переносчика 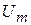 , к которой будет добавляться переменная, изменяющаяся пропорционально модулирующему сигналу:
, к которой будет добавляться переменная, изменяющаяся пропорционально модулирующему сигналу:
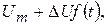
где 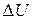 - наибольшее отклонение амплитуды АМ-колебания.
- наибольшее отклонение амплитуды АМ-колебания.
С учетом этого АМ-колебание запишется
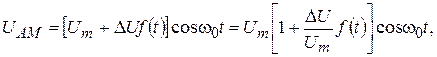 (2.12)
(2.12)
где отношение 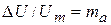 называется коэффициентом амплитудной модуляции. Во избежание перемодуляции, когда на выходе модулятора резко расширяется спектр модулирующего сигнала,
называется коэффициентом амплитудной модуляции. Во избежание перемодуляции, когда на выходе модулятора резко расширяется спектр модулирующего сигнала, 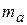 не должен превышать единицы.
не должен превышать единицы.
Выражение (2.12) можно записать так:
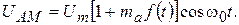 (2.13)
(2.13)
Если модулирующая функция представляет собой гармоническое колебание одной частоты с единичной амплитудой 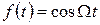 (рис. 2.9, а), то при AM согласно (2.10)
(рис. 2.9, а), то при AM согласно (2.10)
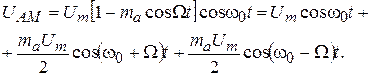 (2.14)
(2.14)
Здесь первое слагаемое описывает не модулируемое колебание несущей частоты, второе и третье слагаемое с частотами 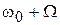 и
и 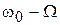 называются соответственно верхней и нижней боковыми частотами. На рис. 2.9, б представлен график напряжения несущей частоты, модулированного по амплитуде по закону информационного сигнала
называются соответственно верхней и нижней боковыми частотами. На рис. 2.9, б представлен график напряжения несущей частоты, модулированного по амплитуде по закону информационного сигнала 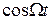 . Спектр АМ-сигнала для рассматриваемого случая, который можно получить, используя преобразование Фурье, содержит несущую и две боковые частоты (рис. 2.9, в). Ширина спектра при этом равна
. Спектр АМ-сигнала для рассматриваемого случая, который можно получить, используя преобразование Фурье, содержит несущую и две боковые частоты (рис. 2.9, в). Ширина спектра при этом равна 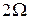 .
.
При модуляции несущей частоты сложным сигналом, имеющим широкий спектр частот, АМ-колебание будет содержать верхнюю и нижнюю боковые полосы частот (рис. 2.9, г). При этом ширина спектра определяется значением удвоенной максимальной частоты спектра модулирующего сигнала
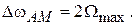
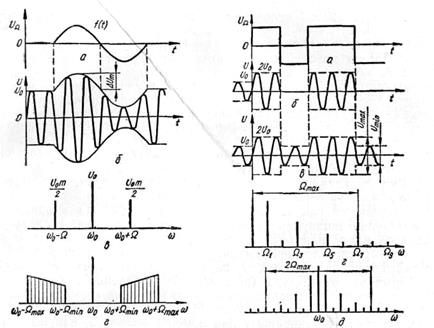
| Рис. 2.9. Графики модулирующего (а) и модулированного (б) сигналов; спектры амплитуд амплитудно-модулированных сигналов для простого (в) и сложного (г) модулирующих сигналов. | Рис. 2.10. Амплитудная манипуляция: а – модулирующий сигнал; б – амплитудно-манипулированный сигнал при 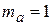 ; в – при ; в – при 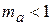 ; г – спектр модулирующего сигнала; д – спектр амплитудно-манипулированного сигнала. ; г – спектр модулирующего сигнала; д – спектр амплитудно-манипулированного сигнала.
|
Занятие 3
Частотная модуляция
При частотной модуляции амплитуда модулируемого напряжения остается постоянной, а частота 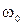 несущей частоты изменяется во времени относительно своего центрального значения по закону изменения первичного сигнала f(t):
несущей частоты изменяется во времени относительно своего центрального значения по закону изменения первичного сигнала f(t):
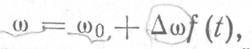 (2.15)
(2.15)
где 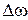 — наибольшее отклонение угловой частоты
— наибольшее отклонение угловой частоты 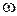 от центрального значения
от центрального значения 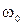 , называемое девиацией частоты.
, называемое девиацией частоты.
Отношение 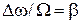 называется индексом частотной модуляции. Так как в выражение для модулируемого сигнала входит постоянная частота, то амплитуду колебания переносчика можно описать выражением
называется индексом частотной модуляции. Так как в выражение для модулируемого сигнала входит постоянная частота, то амплитуду колебания переносчика можно описать выражением
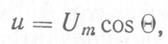 (2.16)
(2.16)
где 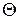 — фаза колебания, связанная с частотой соотношением
— фаза колебания, связанная с частотой соотношением
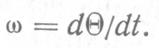
Форма ЧМ-сигнала с постоянной амплитудой представлена на рис. 2.11, а. При ЧМ фаза колебания
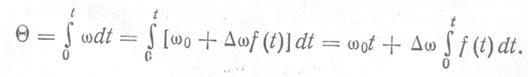 (2.17)
(2.17)
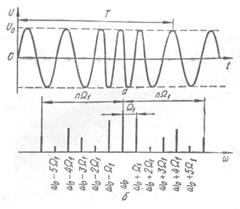 Рис. 2.11. Частотно-модулированный сигнал (а) и его спектр (б)
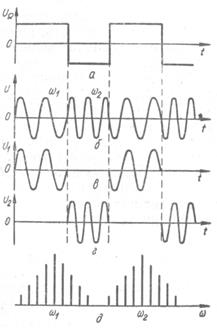
Рис. 2.12. Частотная манипуляция:
а - модулирующий сигнал, б -частотно-манипулированный сигнал, в и г – амплитудно-манипулированные сигналы, д – спектр частотно-манипулированного сигнала.
Рис. 2.11. Частотно-модулированный сигнал (а) и его спектр (б)
Рис. 2.12. Частотная манипуляция:
а - модулирующий сигнал, б -частотно-манипулированный сигнал, в и г – амплитудно-манипулированные сигналы, д – спектр частотно-манипулированного сигнала.
| 
|
Подставив выражение (2.17) в (2.16), получим
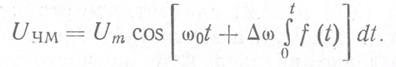 (2.18)
(2.18)
При модуляции несущей модулирующим колебанием одной частоты 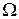 спектр ЧМ-сигнала (рис. 2.11, б), как и при АМ, состоит из несущей частоты и двух боковых полос, но каждая боковая полоса содержит бесконечную последовательность гармонических колебаний, отстоящих друг от друга на
спектр ЧМ-сигнала (рис. 2.11, б), как и при АМ, состоит из несущей частоты и двух боковых полос, но каждая боковая полоса содержит бесконечную последовательность гармонических колебаний, отстоящих друг от друга на 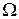 , причем амплитуда k-го колебания (k=1, 2, 3,...), считая от модулируемого сигнала
, причем амплитуда k-го колебания (k=1, 2, 3,...), считая от модулируемого сигнала 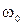 , пропорциональна значению функции Бесселя
, пропорциональна значению функции Бесселя 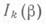 первого рода k-го порядка при аргументе, равном индексу частотной модуляции
первого рода k-го порядка при аргументе, равном индексу частотной модуляции 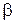 .
.
Так как амплитуда боковых составляющих убывает по мере удаления от несущей частоты, то практически ширину спектра всегда ограничивают частотными составляющими, амплитуды которых не меньше некоторой определенной величины (5—10% амплитуды несущей частоты V т до модуляции).
Приближенно ширину спектра ЧМ-сигнала можно определить из выражения
 (2.19)
(2.19)
Видно, что чем меньше индекс частотной модуляции 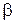 , тем уже практически необходимый спектр ЧМ-сигнала.
, тем уже практически необходимый спектр ЧМ-сигнала.
В зависимости от выбранного индекса модуляции 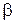 различают узкополосную частотную модуляцию с малыми индексами
различают узкополосную частотную модуляцию с малыми индексами 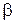 и широкополосную — с большими индексами
и широкополосную — с большими индексами 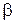 . При узкополосной ЧМ ширина спектра приближается к АМ, а при широкополосной — много больше, чем при АМ.
. При узкополосной ЧМ ширина спектра приближается к АМ, а при широкополосной — много больше, чем при АМ.
Основным преимуществом широкополосной ЧМ является высокая помехоустойчивость, значительно большая, чем при АМ, так как частота сигнала менее подвержена действию помех, чем, амплитуда.
При частотной манипуляции в качестве информационного сигнала используется последовательность прямоугольных импульсов (рис. 2.12, а). При этом ЧМ-сигнал имеет два граничных значения частоты: 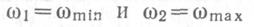 (рис. 2.12, б). Если представить ЧМ-сигнал суммой двух сигналов U1и U2 самплитудной манипуляцией (рис. 2.12, в, г), то легко определить спектр сигнала при частотной манипуляции (рис 2.12, д).
(рис. 2.12, б). Если представить ЧМ-сигнал суммой двух сигналов U1и U2 самплитудной манипуляцией (рис. 2.12, в, г), то легко определить спектр сигнала при частотной манипуляции (рис 2.12, д).
Необходимая ширина спектра частотно-манипулированного сигнала будет равна 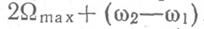 , что больше, чем при амплитудной манипуляции на величину
, что больше, чем при амплитудной манипуляции на величину 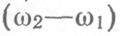 .
.
Фазовая модуляция
При фазовой манипуляции (ФМ) по закону первичного сигнала изменяется начальная фаза модулируемого (несущего) сигнала:
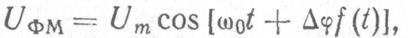 (2.20)
(2.20)
где 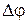 — индекс фазовой модуляции.
— индекс фазовой модуляции.
Из сравнения (2.18) и (2.20) следует, что структура спектра при -ФМ такая же, как при ЧМ, а за ширину боковой полосы спектра принято произведение индекса ФМ на частоту модулирующего сигнала. Таким образом, полная ширина спектра при ФМ
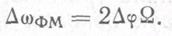
В последнее время все большее значение для передачи дискретной информации приобретает фазовая манипуляция, которую различают по кратности.
В простейшем случае фазы несущего колебания,соответствующие токовой и бестоковой посылкам, или положительному и отрицательному импульсам (рис. 2.13, а), отличаются при фазовой манипуляции на 1800 (рис. 2.13, б). Такая манипуляция получила название однократной.
Зная спектр сигнала при амплитудной манипуляции последовательностью прямоугольных двухполярных импульсов, нетрудно найти спектр при однократной фазовой манипуляции. Так, если к фазоманипулированному сигналу (рис. 2.13, 6) добавить немодулированное несущее колебание U0той же частоты 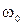 амплитуды U0, совпадающее по фазе, например с колебаниями при положительных импульсах (рис. 2.13, в), то получится амшштудно-манипулированный сигнал с амплитудой 2U0(рис. 2.13, г). Следовательно, спектр фазоманипулированного сигнала будет соответствовать спектру амплитудно-манипулированного сигнала. При этом необходимо увеличить вдвое амплитуды всех боковых составляющих и исключить колебание несущей частоты (рис. 2.13, д, где
амплитуды U0, совпадающее по фазе, например с колебаниями при положительных импульсах (рис. 2.13, в), то получится амшштудно-манипулированный сигнал с амплитудой 2U0(рис. 2.13, г). Следовательно, спектр фазоманипулированного сигнала будет соответствовать спектру амплитудно-манипулированного сигнала. При этом необходимо увеличить вдвое амплитуды всех боковых составляющих и исключить колебание несущей частоты (рис. 2.13, д, где 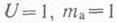 )
)
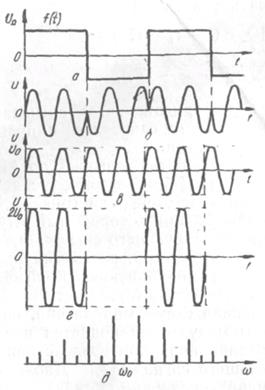
Рис. 2.13. Фазовая манипуляция

Кроме однократной фазовой манипуляции различают также двукратную (через 90°), трехкратную (через 60°), четырехкратную (через 45°) и другие виды фазовой манипуляции. Однако практическое применение в технике передачи данных получили в основном одно-, двух- и трехкратные виды манипуляции.
Занятие 4






