ВСЕ ФОРМУЛЫ ЕГЭ.
Арифметика
Обыкновенные дроби:
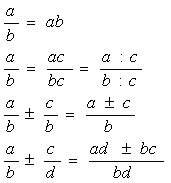

Пропорции:

Процент - сотая часть числа.
Основные задачи на проценты:
1) Найдите число b,составляющее p%> от числа a.
Ответ: 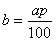
2) Найдите число a, если его p% равны числу b.
Ответ: 
3) Сколько процентов число b составляет от числа a.
Ответ: 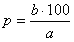 .
.
Законы сложения и умножения чисел
| Переместительный | a + b = b + a; ab = ba |
| Сочетательный | (a + b) + c = a + (b + c); (ab) c=a (bc) |
| Распределительный | (a + b)c=ac + bc |
Степени и корни
Определения:


Действия со степенями. Основные формулы.



Действия с корнями:
(a,b>0): 
 .
.
Формулы сокращенного умножения
1) (а + в)² =а²+2ав+в² - квадрат суммы;
2) (а - в)² =а² -2ав+в² - квадрат разности;
3) (а + в)³ =а³+3а²в+3ав² +а³ - куб суммы;
4) (а - в)³ =а³-3а²в+3ав² - в³ - куб разности;
5) а² - в² =(а-в) (а+в) - разность - квадратов;
6) а³ - в³ =(а – в) (а²+ав +в²) - разность кубов;
7) а³ + в³ =(а+в) (а²-ав+в²) - сумма кубов;
8) (а+в+с)² =а²+в²+с²+2ав+2ас+2вс - квадрат трехчлена;
9) 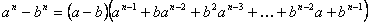 .
.
Уравнения
Линейное уравнение:

Решение:  .
.
Система линейных уравнений: 
Обозначения: 
1) 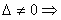 одно решение:
одно решение: 
2)  бесконечно много решений.
бесконечно много решений.
3) 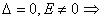 нет решений.
нет решений.
Квадратное уравнение:
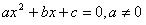
Обозначение:  - дискриминант.
- дискриминант.
1) 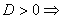 два решения:
два решения:  .
.
2)  одно решение:
одно решение: 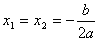 .
.
3)  нет решений.
нет решений.
Разложение квадратного трехчлена на множители:
 .
.
Теорема Виета:
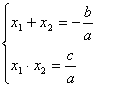
Выделение полного квадрата: 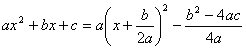 .
.
Биквадратное уравнение: 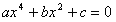 заменой
заменой  сводится к квадратному уравнению:
сводится к квадратному уравнению:  .
.
Неравенства
Свойства неравенств:
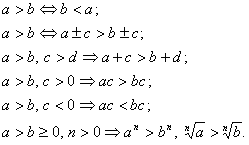
Линейное неравенство:
ax > b,  .
.
Решение:
1) 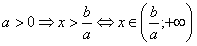 ,
,
2) 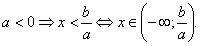
Квадратное неравенство:

Обозначения: 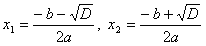 - корни квадратного уравнения
- корни квадратного уравнения 
При 
Решение:
1) 
2) 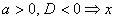 -любое число
-любое число
3)  ,
,
4)  нет решений.
нет решений.
Модули

Свойство модулей:
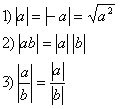
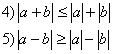
Логарифмы
Логарифм числа b по основанию a:  .
.
Десятичный логарифм: 
Натуральный логарифм: 

Основное логарифмическое тождество: 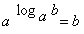 .
.
Свойства логарифмов: (a, b, c >0).

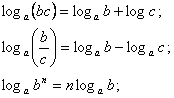

Логарифмические и показательные уравнения и неравенства обычно решаются путем приведения всех выражений, содержащих логарифмические и показательные функции, к одному основанию и последующей замены неизвестной, сводящей задачу к решению алгебраического уравнения или неравенства.
При решении неравенства используют свойства:

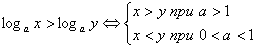
Прогрессии
Определения
Арифметическая прогрессия - последоватльность чисел  , где каждый последующий член получается из предыдущего прибавлением одного и того же числа d (разность прогрессии).
, где каждый последующий член получается из предыдущего прибавлением одного и того же числа d (разность прогрессии).
Геометрическая прогрессия - последовательность чисел  , где каждый последующий член получается из предыдущего умножением на одно и то же число q (знаменатель прогрессии).
, где каждый последующий член получается из предыдущего умножением на одно и то же число q (знаменатель прогрессии).
Формулы членов прогрессии
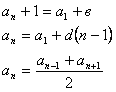

Формулы разности и знаменателя

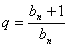
Формулы суммы n первых членов прогрессии


Формула суммы бесконечной убывающей геометрической прогрессии

Тригонометрия
Основные тригонометрические функции
1 радиан 
Простейшие соотношения:
1) Основное тригонометрическое тождество: 
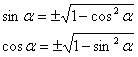
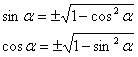



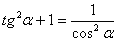
2) Так как  , то
, то

Свойства тригонометрических функций:


Знаки тригонометрических функций:
| Угол |  1 четверть
1 четверть
|  2 четверть
2 четверть
| 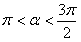 3 четверть
3 четверть
|  4 четверть
4 четверть
|

| + | + | - | - |
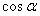
| + | - | - | + |
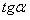
| + | - | + | - |
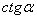
| + | - | + | - |
Некоторые значения:
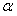
| 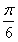
| 
| 
| 
| 
| 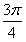
| 
| 
| 
| 
| 
| 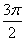
| 
| 
| 
| 
| |

| 
| 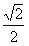
| 
| 
| 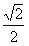
| 
| 
| 
| 
| 
| 
| 
| 
| ||||
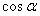
| 
| 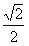
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 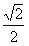
| 
| ||||
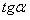
| 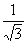
| 
| 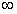
| 
| 
| 
| 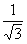
| 
| 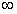
| 
| 
| 
| |||||
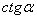
| 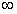
| 
| 
| 
| 
| 
| 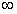
| 
| 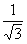
| 
| 
| 
| 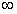
|
Основные тригонометрические формулы
Формулы приведения
| Функция | Угол | |||

| 
| 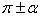
| 
| |
| sin | 
| 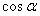
| 
| 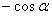
|
| cos | 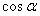
| 
| 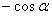
| 
|
| tg | 
| 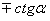
| 
| 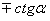
|
| ctg | 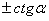
| 
| 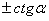
| 
|






