Логических элементов И-НЕ или ИЛИ-НЕ

 

Рассмотрим методику синтеза системы управления в базисе элементарных логических элементов на конкретном примере минимизации переключательных функций с помощью диаграмм Вейча.

Пусть задана переключательная функция четырех аргументов, которая равна 1 на 0, 1, 2, 4, 8, 10, 11, 12, 14, 15 наборах. Необходимо составить и минимизировать данную переключательную функцию с помощью диаграмм Вейча. Решение этой задачи проведем в следующем порядке.

1. По заданному набору переключательной функции составим таблицу истинности.

 

Таблица 3 – Таблица истинности заданной переключательной функции

i	x4	x3	x2	x1	y

 

2. По полученной таблице истинности составим совершенную дизъюнктивную нормальную форму (СДНФ) переключательной функции:

 

(9)

 

3.

Построим диаграмму Вейча данной переключательной функции. В верхнем левом углу каждой клетки диаграммы Вейча запишем номер клетки i. Согласно таблице истинности заполним каждую клетку диаграммы Вейча единицами и нулями (рис.11).

4. Выделим на диаграмме Вейча 1-кубы максимального размера. Таких куба четыре: куб А – клетки с номерами 0,2,8,10; куб В – клетки с номерами 0,1; куб С – клетки с номерами 10,11,14,15; куб D – клетки с номерами 0,4,8,12.

5. Кубу А соответствует контерм , поскольку он находится на пересечении Х₃⁰ и Х₁⁰. Кубу В соответствует контерм 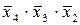, поскольку он находится на пересечении Х₄⁰, Х₃⁰ и Х₂⁰. Кубу С соответствует контерм , поскольку он находится на пересечении Х₄¹ и Х₂¹. Кубу D соответствует контерм , поскольку он находится на пересечении Х₂⁰ и Х₁⁰.

При затруднении при определении контерм можно воспользоваться следующим методом. Например, для куба А выпишем в столбик номера всех клеток, которые занимает куб в двоичном виде:

 

х4	х3	х2	х1	Номер клетки

 

Как видно колонки х₃ и х₁ имеют одинаковое значение, равное 0, что противоположно 1 кубу, поэтому контерм куба А равен .

Для куба С аналогічно получим:

 

х4	х3	х2	х1	Номер клетки

 

Как видно колонки х₄ и х₂ имеют одинаковое значение, равное 1, что соответствует 1 кубу, поэтому контерм куба С равен .

6. Тогда минимизированная дизъюнктивная нормальная форма (МДНФ) данной переключательной функции:

(10)

Для схемной реализации соответствующей логической функции в смешанном базисе необходимо использовать один четырехвходовый элемент ИЛИ, два двухвходовых элемента И, один трехвходовый элемент И и четыре элемента НЕ.

7. Для получения минимизированной нормальной формы (МНФ) переключательной функции в едином базисе И-НЕ, необходимо использовать следующее соотношение:

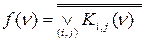
(11)

Тогда преобразуя МДНФ переключательной функции, описываемой выражением (10), с помощью выражения (11), можно получить МНФ в базисе И-НЕ:

(12)

Для схемной реализации такой функции необходимо использовать девять элементов И-НЕ (рис.12).

8.

Для получения МНФ в базисе ИЛИ-НЕ необходимо после нахождения МДНФ (см.п.6) преобразовать ее в минимизированную конъюнктивную нормальную форму (МКНФ) для чего надо найти МДНФ инверсной функции , т.е. найти минимальное покрытие всех 0-клеток функции . Для нахождения МКНФ переключательной функции необходимо воспользоваться законом двойственности, установленного Шенноном:

, (13)

согласно которому инверсию любой функции можно получить взаимной заменой переменных х_р и их инверсией и операций дизъюнкции и конъюнкции.

Для нашего примера после преобразования МДНФ переключательной функции (10) с помощью выражения (13) получим МКНФ данной переключательной функции:

(14)

9. Для получения минимизированной нормальной формы (МНФ) переключательной функции в едином базисе ИЛИ-НЕ, необходимо использовать следующее соотношение:

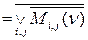(15)

Тогда преобразуя МКНФ переключательной функции, описываемой выражением (14), с помощью выражения (15), можно получить МНФ в базисе ИЛИ-НЕ:

(16)

Для схемной реализации такой функции необходимо использовать семь элементов ИЛИ-НЕ (рис.13).

 

Список рекомендуемой литературы

 

1. Гутников В.С. Интегральная электроника в измерительных устройствах. Л: Энергоатомиздат, 1988.-304 с.

2. Бирюков С.А. Применение цифровых микросхем серий ТТЛ и КМОП. М.: ДМК,1999. – 240 с

3. Пухальский Г.И., Новосельцева Т.Я. Проектирование дискретных устройств на интегральных микросхемах: Справочник. – М.: Радио и связь, 1990. – 304 с.

4. Михайлов С.А. Цифровые устройства и микропроцессоры для морской электроники. – Одесса: ОНМА, 2004. – 176 с.

5. Завадский В.А., Михайлов С.А. Элементная база судовой электронной аппаратуры: Учебное пособие, Одесса: ОНМА, 2006. – 309

6. Схемотехника электронных систем. Аналоговые и цифровые устройства./Бойко В.И., Гуржий А.Н., Жуйков В.Я., Зорин А.А., Спивак В.М./ - СПб.:БХВ-Петергбург, 2004. – 496 с

7. Аналоговые и цифровые интегральные схемы. Под ред. С.В. Якубовского – М.: Высшая школа, 1984. – 432 с.

8. Хоровец П., Хилл У. Искусство схемотехники. В 2-х т. – М.: Мир. 1984. – 590 с.

9. Сайт фирмы Texas Instrument: www.ti.com

10. Сайт фирмы Atmel: www.atmel.com

11. Сайт фирмы linear technology: www.linear.com

12. Сайт фирмы Maxim: www.maxim-ic.com

13. Сайт фирмы Analog device: www.analog. com

14. Иванов В.И., Аксенов А.И., Юшин А.М. Полупроводниковые оптоэлектронные приборы: Справочник. – М.: Энергоатомиздат, 1988. – 448 с.

15. Кауфман М., Сидман А. Практическое руководство по расчётам схем в электронике. В 2 т. – М.: Энергоатомиздат, 1992. – 368 с.

16. Шило В.Л. Популярные цифровые микросхемы: Справочник. – М.: Радио и связь, 1987. – 352 с.

17. Федорков Б.Г., Телец В.А., Дегтяренко В.П. Микроэлектронные цифроаналоговые и аналогово-цифровые преобразователи.- М.: Радио и связь, 1984. – 120 с.

18. Усатенко С.Т., Каченюк Т.К., Терехова М.В. Графическое изображение электрорадиосхем: Справочник. – Киев: Техніка, 1986. – 120 с.

19. Разработка и оформление конструкторской документации радиоэлектронной аппаратуры: Справочник / Под ред.Э.Т. Романычевой. – М.: Радио и связь, 1989. – 448 с.

20. Ашихмин А.С. Цифровая схемотехника. Современный подход. – М.: ТехБук, 2007. – 288 с.

21. Угрюмов Е.П. Цифровая схемотехника.- СПб.: БХВ-Сант-Петербург, 2002. – 528 с.

22. Шило В. Л. Популярные микросхемы КМОП: Справочник. – М.: Горячая линия- Телеком, 2001. – 112 с.

23. Бойт К. Цифровая электроника. – М.: Техносфера, 2007. – 472 с.

24. Музылива И. Элементная база для построения цифровых систем управления. – М.: Техносфера, 2006. – 326 с.

25. Партала О.Н. Цифровая электроника. – М.: Наука и техника, 2002. – 224 с.

 

ПРИЛОЖЕНИЯ

Приложение А

Образец титульного листа

____

Міністерство освіти і науки України

Одеська національна морська академія

 

Кафедра морської електроніки

 

Проектування цифрового реєструвального пристрою

 

РГР

по дисципліні „Цифрові пристрої ”

 

Виконав

курсант гр.3131

______________

№ залікової книжки: _____________

 

Перевірив

 

_______________

 

 

Одеса 2011

Приложение Б