по выполнению контрольной работы № 2.

Теория электрических цепей

 

Задания к контрольной работе № 1 и № 2

с краткими методическими указаниями

для студентов-заочников 1 курса специальности 210420

«Техническая эксплуатация транспортного радиоэлектронного оборудования

(по видам транспорта)»

 

Ухта, 2012 г.

Одобрена цикловой комиссией Составлена в соответствии с Госу-

210420 Техническая эксплуатация дарственными требованиями к ми-транспортного радиоэлектронного нимуму содержания и уровню

оборудования (по видам транспорта) подготовки выпускника по специ-

альности 210420

Председатель

___________ Хрущёва В.Г. Заместитель директора по учебной

работе

Протокол №___ от

_______________ Коротаева Т.М.

«___»___________2012 г.

«___»_________________ 2012 г.

 

Автор:

Кислицын Н.А. – преподаватель УТЖТ – филиала ПГУПС

 

Рецензент:

Мошкина Т.В. – преподаватель спецдисциплин УТЖТ – филиала ПГУПС

 

Пояснительная записка

 

Студенты специальности 210420 «Техническая эксплуатация транспортного радиоэлектронного оборудования (по видам транспорта)» по дисциплине «Теория электрических цепей» выполняют 2 контрольные работы.

Программа дисциплины «Теория электрических цепей» предусматривает изучение физических процессов, происходящих в электрических и магнитных полях, в электрических цепях постоянного и переменного тока, методов расчета электрических цепей, устройств электрических машин постоянного и переменного тока, а также переходных процессов в линейных электрических цепях.

После изучения материала каждого задания студенты выполняют контрольную работу. Все задания на домашние контрольные работы составлены в 50 вариантах. Вариант контрольной работы определяется двумя последними цифрами шифра студента. Замена варианта не разрешается. Ниже приводится таблица вариантов. Она действительна для обеих контрольных работ.

Программой предусмотрено выполнение лабораторных работ. Их цель – закрепить теоретический материал, а также приобрести практические навыки измерения электрических величин и составления схем электрических цепей.

Лабораторные работы выполняются в сроки, предусмотренные учебным графиком. Явка на лабораторные работы обязательна.

Для студента – заочника самостоятельная работа с учебником является основным методом изучения дисциплины. Учеба должна быть систематической и проводиться по индивидуальному плану, составленному самим студентом.

 

На экзамен студент должен представить:

 

1. Зачтенные контрольные работы с выполненной работой над ошибками.

2. Зачтенные отчеты по лабораторным работам.

 

Порядок выполнения и оформления контрольных работ:

1. Каждая контрольная работа должна быть выполнена в срок, указанный в учебном графике, в отдельной тетради в клетку.

2. Условия задачи записываются полностью перед ее решением. Далее записывается краткое условие задачи.

3. Схемы и чертежи выполняются карандашом с помощью чертежных инструментов с соблюдением ГОСТ и Стандартов.

4. По ходу решения всех задач надо записывать краткие пояснения.

5. Векторные диаграммы и графики должны быть построены в масштабе на миллиметровой бумаге или на бумаге в клетку и иметь размеры не менее 10х10 см. Принятые масштабы должны быть указаны.

6. В конце работы следует указать список литературы, используемой при выполнении работы, поставить дату и свою подпись.

7. Небрежно выполненные работы возвращаются без проверки.

 

Без предъявленных зачтенных контрольных и лабораторных работ студент к сдаче экзамена не допускается.

 

Литература:

1. Частоедов Л.И. Электротехника. Учебное пособие для техникумов ж/д транспорта. М.: Маршрут, 2006 г.

2. Данилов И.А., Иванов П.М. Общая электротехника с основами электроники. М: Высшая школа, 2000 г.

3. Евдокимов Ф.Е. Теоретические основы электротехники. М.: Высшая школа, 1981 г.

4. Берёзкина Т.Ф., Гусев Н.Г., Масленников В.В. Задачник по общей электротехнике с основами электроники. М.: Высшая школа, 1998 г.

 

Таблица вариантов.

 

Две послед ние цифры шифра	№ вари- анта	Номера задач	Две послед ние цифры шифра	№ вари- анта	Номера задач
01 51		1 7 13 19 25 31	26 76		6 12 15 24 26 34
02 52		2 8 14 20 27 32	27 77		5 7 13 19 27 31
03 53		4 9 15 21 29 34	28 78		4 8 17 20 25 33
04 54		3 10 16 22 26 33	29 79		3 9 14 21 30 32
05 55		5 11 17 23 28 36	30 80		2 10 15 22 27 36
06 56		6 12 18 24 30 35	31 81		1 11 17 24 28 35
07 57		1 8 14 19 26 32	32 82		3 8 16 23 29 31
08 58		2 7 16 20 29 33	33 83		4 7 18 20 30 32
09 59		4 10 15 22 30 31	34 84		5 10 14 21 28 33
10 60		5 9 18 21 27 34	35 85		6 9 13 22 27 35
11 61		6 11 17 23 25 36	36 86		1 11 16 23 26 34
12 62		3 12 13 24 28 35	37 87		2 12 15 19 25 36
13 63		2 8 16 19 30 32	38 88		5 8 17 21 29 32
14 64		1 10 17 24 28 33	39 89		4 12 18 24 30 34
15 65		4 9 18 23 29 34	40 90		6 8 14 19 28 35
16 66		5 11 13 20 25 35	41 91		3 9 18 23 27 36
17 67		3 7 17 19 26 31	42 92		1 10 15 23 26 32
18 68		6 12 14 21 30 36	43 93		2 11 16 21 26 33
19 69		4 9 16 24 29 32	44 94		2 10 18 22 29 31
20 70		2 11 13 20 30 33	45 95		6 8 17 20 25 34
21 71		1 10 14 19 29 35	46 96		5 11 13 19 27 35
22 72		5 12 15 22 26 36	47 97		1 12 14 24 26 36
23 73		3 7 16 23 27 34	48 98		3 9 15 23 28 32
24 74		6 8 18 21 25 31	49 99		4 8 16 22 25 33
25 75		5 10 17 24 28 31	50 00		6 9 17 20 29 31

 

КОНТРОЛЬНАЯ РАБОТА № 1

Задачи 1 - 6

Два точечных заряда Q₁ и Q₂ расположены в вершинах прямоугольника а и в (рис. 1).

Определить: величину и направление вектора напряженности электрического поля от каждого заряда в одной из вершин и в заданной точке, указанной в задании.

Рассчитать: графическим способом результирующую напряженность и потенциал в этих точках. Как изменится напряженность поля в этих точках, если заряды поместить в диэлектрик?

Данные для своего варианта взять из таблицы.

№ за- дачи	а	в	Q1	Q2	Материал, диэлектрическая проницаемость ε	Заданные точки варианта
см	см	Кл	Кл
			- 6,8.10-11	+4,1.10-11	керамика ε=5,5	3, 5
			-32.10-12	-58.10-12	миканит ε=5,2	4, 8
			+6,3.10-11	+5,5.10-11	слюда ε=6,5	3, 6
			+15.10-12	-23.10-12	полиэтилен ε=2,4	4, 9
			-28.10-12	+37.10-12	эмаль ε=6,8	3, 7
			+4,12.10-11	+6,9.10-12	гетинакс ε= 8	4, 10

Рис. 1.

3 2 см Q₂

2

3 cм 9

8

3 cм 10b

2 cм6

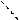5 7 b/2

Q₁ 1 a/2

а 4

Задачи 7 -12

 

На рис. 2 дана схема соединения батареи конденсаторов. Значение ёмкостей конденсаторов и значение одного из напряжений или заряда для своего варианта взять из таблицы.

Вычислить: эквивалентную ёмкость батареи конденсаторов; напряжение сети; напряжение на каждом конденсаторе; общий заряд и заряд на каждом конденсаторе; энергию, накопленную батареей конденсаторов; потенциал заданной точки.

 

№ задач	Емкость конденсатора, мкф	Напряжение или заряд	Потенциал точки схемы
С1	С2	С3	С4	С5
						U = 20 В	А
						Q = 0,72 мКл	В
						U = 25 В	А
						Q = 0,45 мКл	В
						U = 15 В	А
						Q = 0,027 мКл	В

Схема электростатической цепи (рис. 2):

 

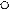
C₁ A C₂ B

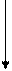
C₃ C₅

U

C₄

 

 

Задачи 13 - 18

 

В цепи, электрическая схема которой изображена на рис. 3, действует один источник

с внутренним сопротивлением R₀. Известны сопротивления всех резисторов, ток в одном из резисторов или напряжение. Данные по своему варианту взять в таблице.

Нарисовать схему цепи в соответствии с исходными данными варианта, на схеме показать направления токов и обозначить эти токи.

Определить: эквивалентное сопротивление цепи; ток в неразветвленной части цепи и токи во всех ветвях цепи; ЭДС источника; мощность в цепи и потенциал точки, указанной в варианте таблицы.

УКАЗАНИЕ. При вычерчивании схемы соблюдать следующие условия: сопротивления, равные нулю, заменить проводом; сопротивления, равные бесконечности, соответствуют разрыву в данном месте цепи. В схеме оставить одну ЭДС, заданную в таблице, а остальные заменить проводом.

 

№ за да чи

Е В

RоОм

R1 Ом

R2 Ом

R3 Ом

R4 Ом

R5 Ом

R6 Ом

R7 Ом

R8 Ом

R9 Ом

R10 Ом

R11 Ом

R12 Ом

допол-нительно

Определить

потенциал

мощность

Е3

∞

I4=0,8А

точ.А

цепи

Е4

∞

1,4

U7=22В

точ.В

на Е4

Е4

∞

U9=72В

точ.А

на R9

Е1

∞

∞

I1=0,2А

точ.В

цепи

Е1

∞

I3=3,4А

точ.А

на Е1

Е2

∞

U2=20В

точ.В

на R3

 

 

Схема электрической цепи (рис. 3):

 

R₁ R₂

R₉

R₇

R₈ E₁ R₁₀

R₃ E₂ R₄

R₁₁ E₃ R₁₂ R₅ E₄ R₆

Задачи 19 - 24

Определить токи во всех ветвях цепи, если ЭДС источников Е₁ и Е₂, их внутреннее

сопротивление R₀₁ и R₀₂, сопротивление резистора R₃. Схема цепи на рис. 4.

 

E₁ E₂

R₀₁ R₀₂

Рис. 4

 

R₁ R₂ R₃

 

 

 

Задачу решить методом, указанным в таблице данных. Проверить решение методом

узлового напряжения. Составить уравнение баланса мощностей. Данные для задачи

приведены в таблице.

 

№ зада чи	Заданные величины
Е1 В	Е2 В	R01 Ом	R02 Ом	R1 Ом	R2 Ом	R3 Ом	Метод решения задачи
			0,1	0,2	3,9	1,9		узловых и контурных уравнений
		84,5	0,2	0,1	7,8	9,9		наложения
			0,01	0,2	1,99	7,98		узловых и контурных уравнений
			0,02	0,05	19,9			наложения
				0,5		3,9		узловых и контурных уравнений
				0,8	9,9			наложения

 

 

Задачи 25 - 30

 

В технике электросвязи используются электромагнитные реле. Принципиальная схема магнитной цепи электромагнитного реле на рис. 5.

 

ℓ₀

 

 

 

 

Lст

 

Рис. 5

Сечение S магнитопровода реле по всей длине одинаково. Число витков катушки w. При притянутом якоре (L_0п) ток I в катушке реле создает магнитный поток Ф с магнитной индукцией В. Принять, что при непритянутом якоре (L₀) Н_ст·L_ст ~0.

Определить индуктивность катушки и силу притяжения якоря электромагнитного реле при притянутом L_0п и непритянутом L₀ якоре. L₀ – средняя линия воздушного зазора, L_ст – длина магнитопровода ферромагнетика по средней линии. Определить также величины, отмеченные в таблице знаком вопроса, при притянутом якоре.

Построить кривую намагничивания ферромагнитного материала, из которого изготовлен магнитопровод, по заданным в таблице значениям напряженности и магнитной индукции:

 

Н, А/см
В, Тл	0,22	0,75	0,93	1,02	1,14	1,28	1,47	1,53	1,57

 

Данные для своего варианта взять из таблицы:

 

№ задачи	Lст мм	L0п мм	L0 мм	S см2	w витков	I А	В Тл	Ф Вб
		0,1	2,7	1,0		?	0,22	?
		0,18	3,1	2,0	?	0,5	?	15.10-5
		0,15	2,8	1,5		?	0,93	?
		0,1	2,75	1,0		?	?	1,02.10-4
		0,16	3,0	2,0	?	0,215	?	44.10-5
		0,17	2,9	1,5		?	0,75	?

 

Задача 31 - 36

На рис. 6 контур авсд образован двумя параллельно расположенными направляющими, электрическим сопротивлением которых можно пренебречь, и двумя проводниками, сопротивлением R₀₁ и R₀₂. Под действием внешней или электромагнитной силы эти проводники могут перемещаться без трения, оставаясь перпендикулярными к направляющим.

Один из проводников сопротивлением R₀₁ движется под действием внешней силы равномерно со скоростью v₁, а другой – R₀₂ под действием электромагнитной силы со скоростью v₂. Однородное магнитное поле направлено на рисунке «на нас», магнитная индукция В. Длина проводников L.

Определить величину и направление тока в контуре, наведенных ЭДС и противо-ЭДС, внешней и электромагнитной сил. На схеме показать направление тока, наведённых ЭДС и всех сил. Составить баланс мощностей.

Данные для своего варианта взять из таблицы.

 

а с

 

B

ℓ R₀₁ R₀₂

 

 

в д

Рис. 6

 

 

Величина	Номер задачи
В, Тл	1,0	1,1	1,2	0,9	0,8	2,0
L, см
v1, м/с		12,5				1,8
v2, м/с					6,5	1,5
R01, Ом	0,1	0,1	0,1	0,2	0,12	0,01
R02, Ом	0,1	0,2	0,3	0,1	0,2	0,01
Внешняя сила двигает провод	левый	правый	левый	правый	правый	левый
вправо	влево	влево	влево	влево	вправо

 

Методические указания

по выполнению контрольной работы № 1

 

Для решения задач № 1 – 6 требуется усвоить основные понятия, характеризующие электрическое поле: напряженность, потенциал, напряжение, диэлектрическая проницаемость.

Напряженность в заданной точке электрического поля, созданного несколькими зарядами, определяется по принципу суперпозиции (наложения), т.е. напряженность поля равна геометрической сумме напряженностей от каждого заряда в отдельности.

Величина напряженности поля заряда в заданной точке определяется по формуле:

E = 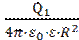, где ε_о = 8,85·10^-12 Ф/м - электрическая постоянная; Q – заряд тела, Кл; ε - относительная диэлектрическая проницаемость среды; R – расстояние от заряда до точки.

Если угол между векторами Е₁ и Е₂ прямой, то напряженность поля в заданной точке находится по теореме Пифагора:

Е = √ Е₁² + Е₂²

Величину напряженности поля в заданной точке можно определить и графически: отложить в выбранном масштабе векторы Е₁ и Е₂; геометрическим сложением векторов

Е₁ и Е₂ получить вектор Е; измерить длину вектора напряженности Е и умножить её на масштаб: Е = ℓ_Е ^. М_Е.

Потенциал поля точечного заряда: φ = Q/4·π·ε_о·ε·R

Если поле образовано несколькими точечными зарядами, то потенциал поля в заданной точке равен алгебраической сумме потенциалов полей, образованных в этой точке каждым зарядом отдельно: φ = ∑φ _i

 

Пример 1. Два точечных заряда 6,7 нКл и -13,3 нКл находятся на расстоянии 5 см друг от друга. Определить напряженность и потенциал электрического поля в точке, расположенной на расстоянии 3 см от положительного заряда и 4 см от отрицательного.

 

Дано: Q₁ = 6,7 нКл = 6,7 ^.10^-9 Кл; Q₂ = -13,3 нКл = -13,3 ^.10^-9 Кл;

R = 5 см = 5^.10^-2 м; R₁ = 3 см = 3^.10^-2 м; R₂ = 4 см = 4^.10^-2 м.

Решение.

1. Так как заряды точечные, то напряженности поля, созданного каждым зарядом:

E₁ = Q₁/ (4π·εo·ε·R₁²) = 6,7^.10^-9.9^.10⁹/1^.(3^.10^-2)² = 67^.10³ В/м;

E₂ = Q₂/ (4π·εo·ε·R₂²) = 13,3^.10^-9. 9^.10⁹/1^.(4^.10^-2)² = 74,8^.10³ В/м.

 

2. Из условия задачи следует, что угол между векторами Е₁ и Е₂ прямой, тогда напряженность поля в точке А находим по теореме Пифагора:

Е = = ==101000 В/м = 101 кВ/м.

Величину напряженности поля в т. А можно определить графическим методом.

 

3. Потенциал электрического поля в т. А:

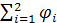= = Q₁/ (4π·εo·ε·R₁) + Q₂ /(4π·εo·ε·R₂) = 9^.10^9. (Q₁/R₁ + Q₂/R₂) =

= 6,7^.10^-9/3^.10^-2 - 13,3^.10^-9/4^.10^-2 = 9^.10^9.10^-7(6,6/3 - 13,3/4) = - 919,8 В.

 

Для решения задач № 7 – 12 необходимо изучить материал «Электрическая ёмкость и конденсаторы».

Нередко возникает необходимость соединять имеющиеся конденсаторы в батареи последовательно, параллельно и смешанно, подбирая конденсаторы по ёмкости и напряжению. Для решения задач необходимо усвоить принципы распределения напряжения и заряда в схемах последовательного и параллельного соединения конденсаторов; знать формулы эквивалентной ёмкости и энергии электрического поля конденсаторов.

В учебном пособии Частоедова рассмотрен пример расчета цепи смешанного соединения конденсаторов.

Рассмотрим пример задачи, когда известно напряжение на одном из конденсаторов.

 

Пример 2. На рис. 7 приведена схема соединения конденсаторов. Определить эквивалентную ёмкость С_экв батареи конденсаторов; общий заряд Q; напряжение сети U, напряжение и заряд на каждом конденсаторе, если известно: С₁ = 24 мкФ; С₂ = С₃ = 8 мкФ; С₄ = 12 мкФ; С₅ = 6 мкФ; напряжение на пятом конденсаторе U₅ = 30 В.

+ •

C₁ C₂ C₄

U C₃ C₅ Рис. 7

 

- •

 

Дано: С₁ = 24 мкФ; С₂ = С₃ = 8мкФ; С₄ = 12 мкФ; С₅ = 6 мкФ; U₅ = 30 В.

Определить: U -?; Q -?; C -?; U₁ -?; U₂ -?; U₃ -?; U₄ -?; Q₁ -?.

 

Решение:

1. Общая ёмкость последовательного соединения конденсаторов С₄ и С₅:

С₄,₅ = С₄^.С₅ / (С₄ + С₅) = 12 ^. 6 / (12 + 6) = 4 мкФ.

2. Общая ёмкость параллельно соединенных конденсаторов С₃ и С₄,₅:

С₃-₅ = С₃ + С₄,₅ = 8 + 4 = 12 мкФ.

3. Общая ёмкость последовательно соединённых конденсаторов С₁, С₂ и С₃-₅, которая и является эквивалентной ёмкостью батареи конденсаторов:

4. По заданному напряжению U₅ и ёмкости конденсаторов С₅ определяем заряд, накапливаемый этим конденсатором:

U₅ = С₅^.U₅ = 6^.10^-6.30 = 180^.10^-6 Кл.

5. Заряд конденсатора С₄ равен Q₄ = Q₅ = Q₄,₅ = 180^.10^-6 Кл, так как конденсаторы С₄ и С₅ соединены последовательно.

6. Напряжение на 4 конденсаторе: U₄ = Q₄ / C₄ = 180^.10^-6 /12^.10^-6 = 15 В.

7. Напряжение на 3 конденсаторе: U₃ = U₄ + U₅ = 15 + 30 = 45 В.

8. Заряд конденсатора С₃: Q₃ = U₃ ^. C₃ = 45 ^. 8^.10^-6 = 360^.10^-6 Кл.

9. Общий заряд батареи и заряды конденсаторов С₁ и С₂:

Q = Q₁ = Q₂ = Q₃-₄ = Q₃ + Q₄,₅ = 360^.10^-6 + 180^.10^-6 = 540^.10^-6 Кл.

10. Напряжение на С₁ и С₂: U₁ = Q / C₁ = 540^.10^-6 / 24^.10^-6 = 22,5 В.

U₂ = Q / C₂ = 540^.10^-6 / 8^.10^-6 = 67,5 В.

11. Напряжение сети (напряжение последовательно соединенных конденсаторов С₁, С₂ и С₃-₄): U = U₁ + U₂ + U₃-₄ = 22,5 + 67,5 + 45 = 135 В.

12. Энергия электрического поля батареи конденсаторов:

W = C ^. U² / 2 = 4^.10 ^{-6 .}135² / 2 = 36,45^.10^-3 Дж.

 

В задачах № 13 -18 необходимо провести расчет простой электрической цепи

со смешанным соединением резисторов. Для их решения необходимо знать закон Ома

и первый закон Кирхгофа.

Рассмотрим решение примера.

 

Пример 3. На рис. 8 приведена схема соединения резисторов и источника энергии. Определить эквивалентное сопротивление цепи R_экв, ток в каждом резисторе, ЭДС

и мощность источника энергии P_ист, потенциал т. А, если известно, что R₁ = 7,5 Ом;

R₂ = 15 Ом; R₃ = 16 Ом; R₄ = 21 Ом; R₅ = 42 Ом; R₀ = 0,5 Ом; U₃ = 32 В.

 

I₃

R₃

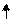I₂ E, R₀ I₅ Рис. 8

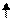
I₄

R₂ I₁

 

R₁ R₄ R₅

 

 

Дано: R₁ = 7,5 Ом R₂ = 15 Ом R₃ = 16 Ом

R₄ = 21 Ом R5 = 42 Ом R₀ = 0,5 Ом U₃ = 32 В

Определить: R_экв, I₁, Е, Р_ист, φ_А

Решение.

 

1. Обозначим стрелками направление токов в каждом резисторе. Индексы токов

и напряжений на каждом резисторе принимаем соответствующими номеру резистора.

2. Эквивалентное сопротивление цепи R_экв определим путем постепенного упрощения –

«свертывания» схемы.

• R₄ и R₅ соединены параллельно, их общее сопротивление равно:

R₄,₅ = R₄^.R₅ / (R₄ + R₅) = 21^.42 / (21 + 42) = 14 Ом;

• R₃ и R₄,₅ соединены последовательно: R₃-₅ = R₃ + R₄,₅ = 16 +14 = 30 Ом;

• R₃-₅ и R₂ соединены параллельно:

R₂-₅ = R₂^.R₃-₅ / (R₂ + R₃-₅) = 15^.30 / (15 + 30) = 10 Ом;

• R₁ и R₂-₅ соединены последовательно: R_экв = R₁-₅ = R₁ + R₂-₅ = 7,5 + 10 = 17,5 Ом.

• По закону Ома для участка цепи определяем ток в резисторе R₃:

I₃ = U₃ / R₃ = 32 /16 = 2 А.

• I₄,₅ = I₃ = 2A, так как R₃ и R₄,₅ соединены последовательно.

• Определяем напряжение на сопротивлении R₄,₅: U₄,₅ = I₃^.R₄,₅ = 2^.14 = 28 B.

• По закону Ома токи в резисторах: I₄ = U₄,₅ / R₄ = 28 /21 = 1,33 A;

I₅ = U₄,₅ / R₅ = 28 /42 = 0,67 A;

• Напряжение на втором резисторе: U₂ = U₃-₅ = U₃ + U₄,₅ = 32 + 28 = 60 B.

• Ток в резисторе: I₂ = U₂ / R₂ = 60 / 15 = 4 A.

• По первому закону Кирхгофа находим ток источника: I₁ = I₂ + I₃ = 4 +2 = 6 A.

• ЭДС источника: E = I₁^. (R_экв + R₀) = 6^.(17,5 + 0,5) = 108 B.

• Мощность источника энергии: P_ист = E ^. I₁ =108 ^. 6 =648 Вт.

 

Задачи № 19 – 24 предусматривают расчет сложной электрической цепи. Сложные цепи имеют несколько источников ЭДС, которые расположены в разных ветвях, и резисторы. Расчет сложной цепи сводится к определению токов во всех ветвях по величине и направлению по заданным ЭДС и сопротивлениям резисторов.

Существует несколько методов расчета сложных цепей. Рассмотрим их применение.

 

Пример 5.

Определить токи во всех ветвях цепи, если ЭДС источников Е₁=180 В, Е₂=96 В, их внутренние сопротивления R₀₁=0,1 Ом, R₀₂=2 Ом; сопротивления резисторов: R₁=7,9 Ом, R₂=20 Ом, R₃=32 Ом, R₄=10 Ом.

Задачу решить методом узловых и контурных уравнений, составленных по законам Кирхгофа. Составить уравнение баланса мощности.

 

B C R₄ K

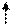I₁ I₃ I₂ E₂

R₁ R₀₂ Рис. 9

R₃

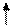I₁ I₃ I₂ R₂

 

D N

 

Метод узловых и контурных уравнений

 

Дано: E₁ = 180 B E₂ = 96 B R₁ = 7,9 Ом R ₃ = 20 Ом

R₀₁ = 0,1 Ом R₀₂ = 2 Ом R ₂ = 32 Ом R₄ = 10 Ом

Определить: I₁, I₂, I₃.

Решение.

Количество неизвестных токов равно количеству ветвей в цепи. На рис. 9 три ветви, следовательно, неизвестных токов три, для их нахождения необходимо составить систему

из трёх уравнений. Алгоритм расчета:

1. Обозначить контуры буквами.

2. На схеме произвольно показать предварительное направление токов (пунктир).

3. Составляем уравнения по первому закону Кирхгофа. Количество этих уравнений равно числу узлов в схеме без одного. На схеме два узла – С и Д, следовательно, составляем одно уравнение по первому закону Кирхгофа, например, для узловой точки С: I₁ + I₂ = I₃.

Остальные уравнения (3 – 1 = 2) составляются по второму закону Кирхгофа, т.е. два уравнения. Второе уравнение составим для контура АВСДА, направление обхода контура «по часовой стрелке»:

E₁ = I₁^. (R₁ + R₀₁) + I₃^.R₃.

Третье уравнение составим для контура СКNДС; направление обхода контура примем

«против часовой стрелки»:

E₂ = I₂^. (R₂ + R₀₂ + R₄) + I₃^.R₃.

4. Подставим исходные данные в полученную систему из трёх уравнений и решим систему относительно неизвестных токов:

I₁ + I₂ = I₃ I₁ + I₂ = I₃ (1)

E₁ = I₁^. (R₁ + R₀₁) + I₃^.R₃ 180 = I₁^. (7,9 + 0,1) + I₃ ^. 32 (2)

E₂ = I₂^. (R₁ + R₀₁ + R₄) + I₃^.R₃ 96 = I₂^. (20 +2 +10) + I₃ ^. 32 (3)

Из второго уравнения получим: 180 = 8^.I₁ + 32^.I₃, отсюда I₁=(180–32^.I₃)/8=22,5–4^.I₃ (а)

Из третьего уравнения получим: 96=32^.I₂+32^.I₃, отсюда I₂ = (96 – 32^. I₃)/32 = 3 – I₃ (б)

Подставим выражения (а) и (б) в первое уравнение и находим ток I₃:

22,5 – 4 ^. I₃ + 3 - I₃ = I₃; 22,5 + 3 = I₃ + 4 ^. I₃ + I₃; 25,5 = 6 ^. I₃; I₃ =25,5/6 = 4,25 A.

Значение тока I₃ подставим в выражения (а) и (б) и определяем токи I₁ и I₂:

I₁ = 22,5 – 4 ^. I₃ = 22,5 – 4 ^. 4,25 = 5,5 A; и I₂ = 3 – I₃ = 3 – 4,25 – 1,25 A.

Ток I₂ получился отрицательным, это значит, что первоначально принятое направление тока I₂ оказалось неверным и должно быть изменено на противоположное.

На схеме показываем действительное направление токов.

 

Пример 6. Определить токи во всех ветвях цепи по исходным данным примера 5 методом наложения.

Метод наложения

Решение.

1. Оставляем в схеме только источник с ЭДС Е₁; а источник с ЭДС Е₂ приравниваем к нулю, но его внутреннее сопротивление в схеме остается (рис. 10).

С R₄

•

E₁ R₀₂

I₁´ I₃´ I₂´

R₀₁

 

R₃

R₁ R₂

D Рис. 10

•

Рассчитывая получившуюся простую схему с одним источником и смешанным соединением резисторов, определяем частичные токи в ветвях, создаваемых в схеме источником Е₁ Показываем направление токов на схеме (рис. 10).

Определяем эквивалентное сопротивление схемы:

 

R´= R₁ + R₀₁ + = 7,9 + 0,1+ = 24 Oм

 

Ток в первой ветви: I´₁ = Е₁ / R´ = 180 / 24 = 7,5 А.

Напряжение между точками С и Д в схеме: U´_СД =E₁–I´₁^.(R₁+R₀₁)=180–7,5^.(7,9 =0,1)=120 B.

Токи во второй и в третьей ветвях: I´₂ = U´_СД / (R₂ + R₀₂ + R₄) = 120 / (20 + 2 + 10) = 3,75 A;

I´₃ = U´_СД / R₃ = 120 / 32 = 3,75 A.

2. Оставляем в схеме только источник Е₂, ЭДС Е₁ приравниваем к нулю, но его внутреннее сопротивление в схеме остаётся (рис.11).

C R₄

´´ I₂´´

 

 

Рис. 11

 

 

Рассчитывая получившуюся простую схему с одним источником и смешанным соединением резисторов, определяем токи ветвей, создаваемые источником Е₂.

Показываем направление токов на схеме. Рассчитываем эквивалентное сопротивление цепи: R´´ = R₂ + R₀₂ + R₄ + (R₁ + R₀₁) ^. R₃ / (R₁ + R₀₁ + R₃) =

= 20 + 2 + 10 + (7,9 +0,1) ^. 32 / (7,9 + 0,1 + 32) = 38,4 Ом.

Ток во второй ветви: I´´₂ = Е₂ / R´´ = 96 / 38,4 = 2,5 А.

Напряжение между точками С и Д в схеме:

U´´_СД = E₂ – I´´₂ ^. (R₂ + R₀₂ + R₄) = 96 – 2,5 ^. (20 + 2 + 10) = 16 B.

Токи первой и третьей ветвей: I´´₁ = U´´_СД / (R₁ + R₀₁) = 16